Adaptive Computation Time
動機づけ
Universal Transformer の論文を読んだ際に気になっていたACT(= Adaptive Computation Time)の論文をメインのところだけざっと読みました。
※Universal TransformerではACTを導入したことにより、精度向上が図れたことが実験結果より裏付けされています。
※ACTの論文ではRNNにACTを適用していますが、Universal TransformerのようにRNNの性質を持つモデルであれば、ACTは適用できると言えます。
元論文
What is ACT?
ACTは簡単にいうと、「各要素における計算回数を要素ごとに最適化させる」ための仕組みとなります。
※自分で書いていて思いましたが、これだと何を言っているかが、さっぱりな気がしますね・・涙
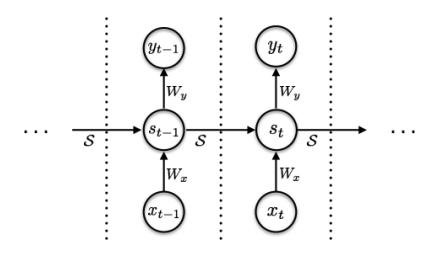
下記の元論文の図を見ると、ちょっと分かりやすくなります。
通常のRNNでは時間軸側(時間軸はtで表されています)では繰り返しの処理を行い、隠れ層のパラメーター調整を行います。
※基本的にRNNの隠れ層の重みは時間軸に置いて、共有されています。
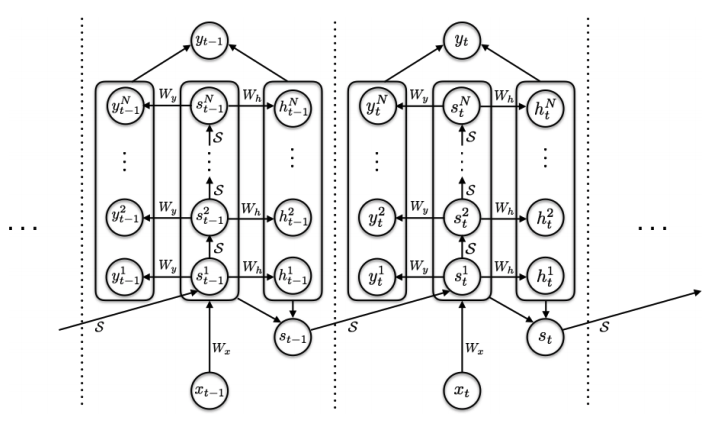
しかし、ACTを導入したRNNでは、各時間軸で縦方向に素子が伸びています。
※繰り返し回数については各素子の右側の数字(1, 2....N)が表しています。
つまり、ACTを導入したRNNでは、「各時間軸(≒ 単語毎)においてのパラメーター調整の回数を最適化されている」と言えます。
RNN?
Recurent Neural Networkの略になります。
時系列データ(例えば文章、行動ログの解析など)の扱いが可能なNeural Networkとなります。
※RNN内部で使われる素子は色々な素子(LSTMとかGRUとか)があります。
RNNの説明については、こちらが参考になります。
ACTの仕組み
では、ACTの仕組みについて、説明していきます。
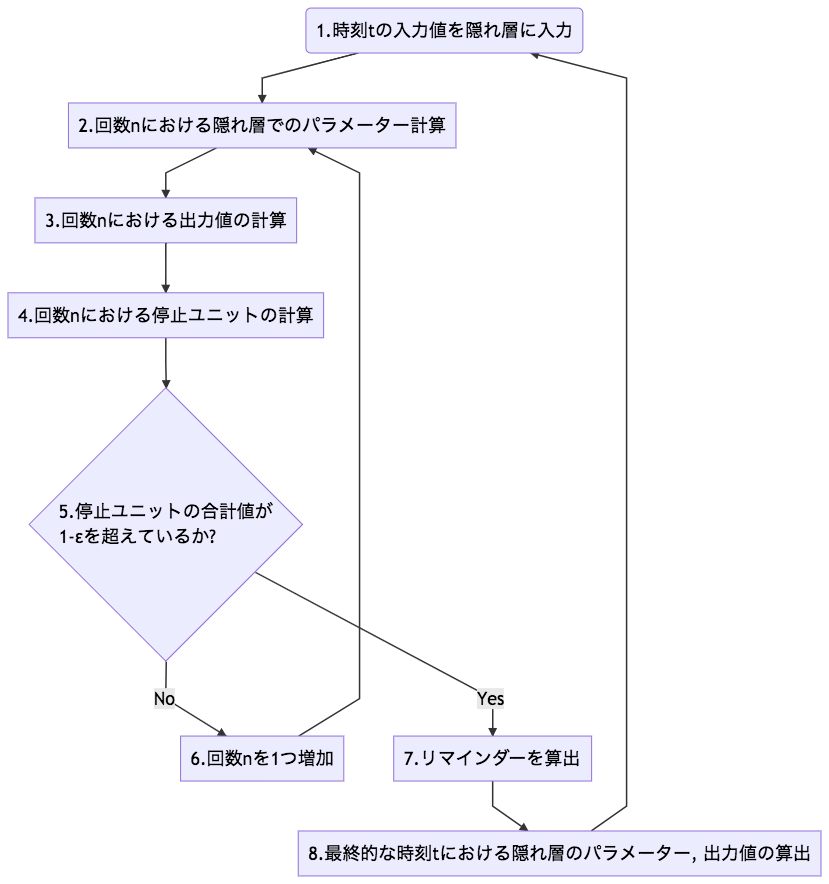
ACTの繰り返し処理の過程
以下のようなフローチャートになります。
※ATOM+mermaid.jsで書いてみましたが、ちょっと図が見にくいかもですね・・。
mermaid自体は結構使いやすいなーと思いました。
各処理における計算は下記となります。
1. 時刻tにおける入力値を隠れ層に入力
初回(繰り返しなし)の入力値を隠れ層に入れます。
※入力値である$x$は各回数nで基本的に同一ですが、
「最初の計算」と「繰り返しの計算」であることがわかるようにフラグを追加しています。
(初回のみはフラグがたっている)
s_t^n = S(s_{t-1}, x_t^1)
2. 回数nにおける隠れ層でのパラメーター計算
n回目の繰り返しにおける隠れ層のパラメーターを計算する
※便宜上、小文字のsは隠れ層で計算された後の出力値(行列)、大文字のSは隠れ層での計算処理(例えば重み行列を乗算するなど)を表します。
s_t^n = S(s_t^{n-1}, x_t^n)
3. 回数nにおける出力値の計算
y_t^n = W_y s_t^n + b_y
4. 回数nにおける停止ユニットの計算
停止ユニットは後述しますが、合算値を利用して、繰り返し処理を続けるか?終わらせるかを判定するために利用します。
停止ユニットの計算式は下記となります。
h_t^n = \sigma (W_h s_t^n + b_h)\\
\sigma(x) = \frac{1}{1 - e^{-x}}
$h_t^n$ は時刻tのn回目計算における停止ユニットの出力値となります。
σはシグモイド関数(活性化関数)を表します。
※シグモイド関数の数式から以下の特性があります。
0 < \sigma(x) < 1
5. 停止ユニットの合計値が1-εを超えているか?
N(t) = min\{n:\sum_{k=1}^{n} h_t^k >= 1-\epsilon\}
なぜ「1」ではなく、「1-ε」を使うか?
これは、「繰り返し回数を1回を許容するため」と言えます。
※仮に「1」で判定してしまうと、sigmoidの特性上必ず2回目の繰り返しが発生します。
なぜなら、1回目の処理のみでは1を超えないためです。
上記の数式は、$\sum_{k=1}^{n} h_t^k >= 1-\epsilon$ を満たす
最小のnを繰り返し回数$N(t)$に設定しています。
上記の条件を満たさない場合は後述の6番へ。
上記の条件を満たす場合は後述の7番へ。
6. 回数nを1つ増加
これはそのままの意味なので省略します。
7. リマインダーを算出
R(t) = 1 - \sum_{n=1}^{N(t)-1}h_t^n
リマインダーは後述のロス関数で利用されますが、
最終的にはこのリマインダーを少なくするように学習処理が進みます。
※詳細は後述します。
ちなみに$R(t)$は必ず$0<R(t)<1$を満たします。
8. 最終的な時刻tにおける隠れ層のパラメーター, 出力値の算出
各回数で隠れ層パラメーター及び出力値が作成されます。
そのため、各回数での値に重みをつけて最終結果とします。
(加重平均を取っている)
まず、各回数での重み(=$p_t^n$)を下記のように設定します。
p_t^n = \left\{
\begin{array}{ll}
R(t) & (n = N(t)) \\
h_t^n & (1 <= n < N(t))
\end{array}
\right.
上記を利用して、最終的な時刻tでの
隠れ層パラメーター(=$s_t$)及び出力値(=$y_t$)を算出します。
※$s_t$については、次の時刻t+1で利用されます。
s_t = \sum_{n=1}^{N(t)}p_t^n s_t^n \\
y_t = \sum_{n=1}^{N(t)}p_t^n y_t^n
ACTを利用した場合の損失関数について
ACTを利用した場合、損失関数が少し変わります。
繰り返し回数の制限について
損失関数が変わる理由ですが、「繰り返し回数に制限をつけるため」となります。
具体的な制限は以下のような式となります。
\rho_t = N(t) + R(t) \\
P(X) = \sum_{t=1}^{T} \rho_t
$X$は入力文字列($x_1, x_2, ...x_T$)となります。
$P(X)$は元論文では「ponder cost」(熟考コスト)と表現されています。
つまり、「繰り返し回数に関するペナルティ」と言い換えれます。
損失関数について
以下のように損失関数は定義されます。
\hat{L}(X,Y) = L(X,Y) + \tau P(X)
$Y$は出力文字列($y_1, y_2, ...y_T$)となります。
$\tau$はハイパーパラメーターで、熟考コストをどの程度損失関数に適用させるか、を示します。
※値が高ければ、熟考コストを上げないようにする働きが強くなるため、計算時間は減りますが、精度が下がります。
※値が低ければ、熟考コストを上げないようにする働きが弱まるため、計算時間は増えますが、精度が上がります。
また、$N(t)$は離散値となり微分不可のため、誤差逆伝搬をする都合で実際には、$N(t)$は無視しているようです。
そのため、誤差逆伝搬をする際には元々のロス関数の勾配と$R(t)$の勾配が伝搬することになります。
実験結果
すいません、、書くのがつかれたので、一つの結果図についてのみ軽く触れます。
★ACTを導入したRNNを利用して、入力の難易度と熟考回数(繰り返し回数)及び精度(エラー率)の関連を示した図(元論文のFigure6)
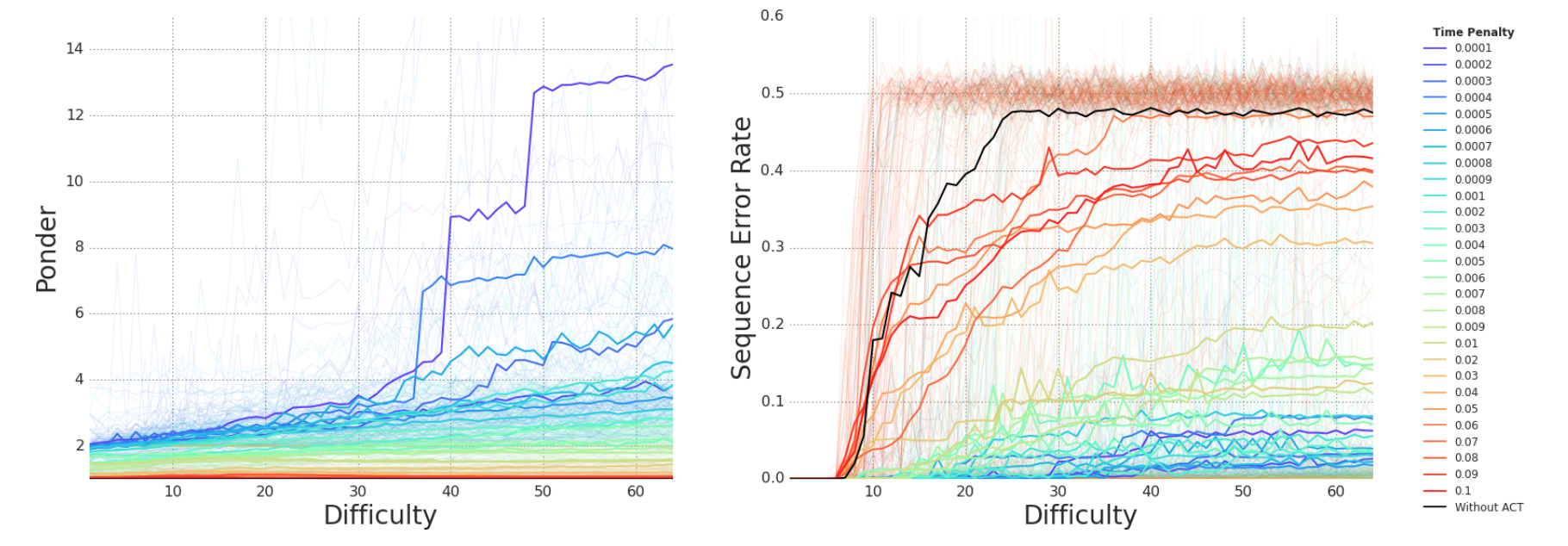
図の右側に記載されている「Time Penalty」は前述した$\tau$の値となります。
この値が高いと「熟考コストは上がるが、精度は下がる」となります。(低い場合は逆)
上記の内容を図(実験結果)が示していると言えます。
参考資料
論文以外で参考にしたサイトです。