はじめに
機械学習の勉強でニューラルネットワークを用いて、手書き数字認識を行いました。
本記事では、ニューラルネットワークとは何ぞやといったところから順を追って解説いたします。
ニューラルネットワーク
ニューロン(脳の神経細胞)が繋がってできる網状の集合体のことを指します。外部より入ってきた情報から瞬時に判断し行動するために必要な働きがあります。自動車を運転する人間で例えると、信号が青になったらアクセルを踏んで進み、信号が赤になったらブレーキを踏んで自動車を停止させます。ここでは、そんなニューラルネットワークを構成するニューロンについて詳しく見ていきます。
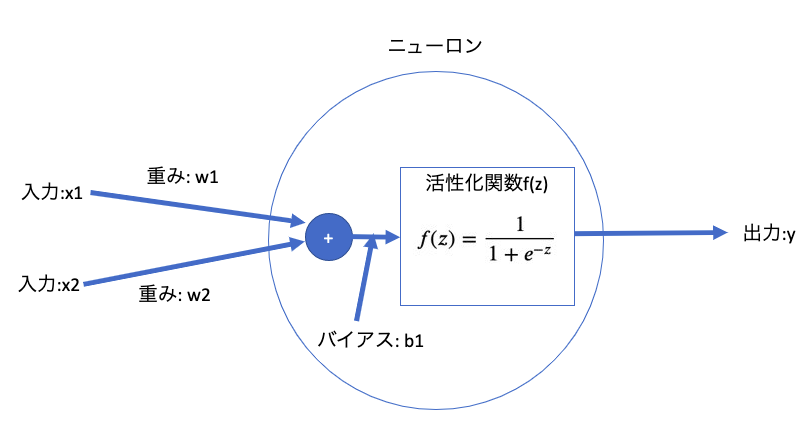
1つのニューロンでは以下の処理が行われている。
- 入力値は$x_1,x_2$
- 重みは$w_1,w_2$
- 各入力値に重みをかけて足し合わせる
- さらにその足し合わせた値にバイアス$b_1$を加える、この値を$z$とする
- 活性化関数に$z$を入力して、その計算結果を$a$とする
- $a$は次のニューロンに入力値として渡される
これが下図のように網目状につながって構成されるのがニューラルネットワークです。

次項目で活性化関数の説明をします。
活性化関数
ただ足し合わせるだけだと、ニューロンから出力される値の表現力が低いままです。そこで用いられるのが活性化関数です。行動のパターンに幅を持たせるイメージです。
活性化関数の種類
- 恒等関数
- ステップ関数
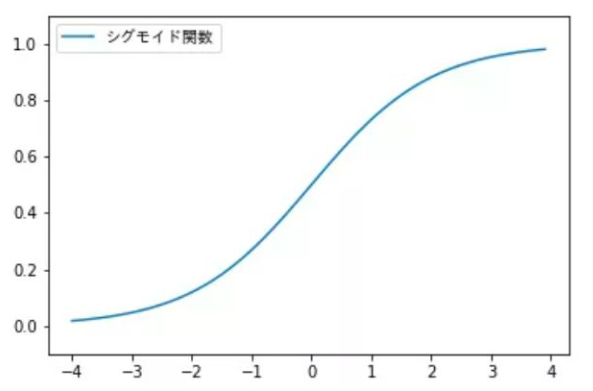
- シグモイド関数 ← CHECK!
- ReLU関数
- ソフトマックス関数 etc...
今回はシグモイド関数を用いるので、シグモイド関数について説明します。
シグモイド関数
シグモイド関数は下記の数式で表されます。
$$
f(z)=\frac{1}{1+e^{-z}} (eはネイピア数です)
$$
次のような性質があります。
- $\lim_{z \to \infty} f(z)\approx1 $
- $\lim_{z \to -\infty} f(z)\approx0 $
- $f(0)=0.5 $
- $f'(z)=f(z)(1-f(z))$
シグモイド関数の微分の導出
$$
f'(z)=\left(\frac{1}{1+e^{-z}}\right)'
$$
$$
\ =\left((1+e^{-z})^{-1}\right)'
$$
$$
\ =\frac{-(1+e^{-z})'}{(1+e^{-z})^{2}}
$$
$$
\ =\frac{e^{-z}}{1+e^{-z}} \times \frac{1}{1+e^{-z}}
$$
$$
\ =\frac{1}{1+e^{-z}} \times \frac{(1+e^{-z})-1}{1+e^{-z}}
$$
$$
\ =\frac{1}{1+e^{-z}} \left(1-\frac{1}{1+e^{-z}}\right)
$$
$$
\ =f(z)(1-f(z))
$$
微分したときに元の式を含めた形で、表されるのもシグモイド関数の特徴です。
コスト関数
正解と予測がどれだけずれているかを表す関数を損失関数といいます。また、過学習を抑制するために重みの値を調整するにわ罰則項が用いられます。この損失関数(第1項)と罰則項(第2項)を合わせた関数をコスト関数といいます。コスト関数は下記の通りです。
$$
J(W)=- \bigl[\sum_{i=1}^{n}\sum_{j=1}^{t} y_j^{[i]}\log(a_j^{[i]})+(1-y_j^{[i]})\log(1-a_j^{[i]})\bigr]+\frac{\lambda}{2}\sum_{l=1}^{L-1}\sum_{i=1}^{u_l}\sum_{j=1}^{u_l+1}(w_{j,i}^{(l)})^2
$$
この関数を最小にするための重み$w$を求める必要があります。そのため、コスト関数を$w$で偏微分して勾配が0になるときの$w$が解になります。
扱うデータ
機械学習ライブラリsklearnで用意されているload_disitsを扱います。
ここには0から9の手書き数字の画像が含まれています。

しかし、画像のままではコンピュータは処理ができないので配列に変換する必要があります。
一枚あたり28x28ピクセルの画像を使用するので、サイズが784(=28x28)の一次元配列に変換します。
配列の各要素には、グレースケールの輝度(きど)が含まれています。
順伝播
ニューラルネットワークがどのようにして、数字を予測するのかを見ていくために順伝播:フォワードプロパゲーションについて解説します。
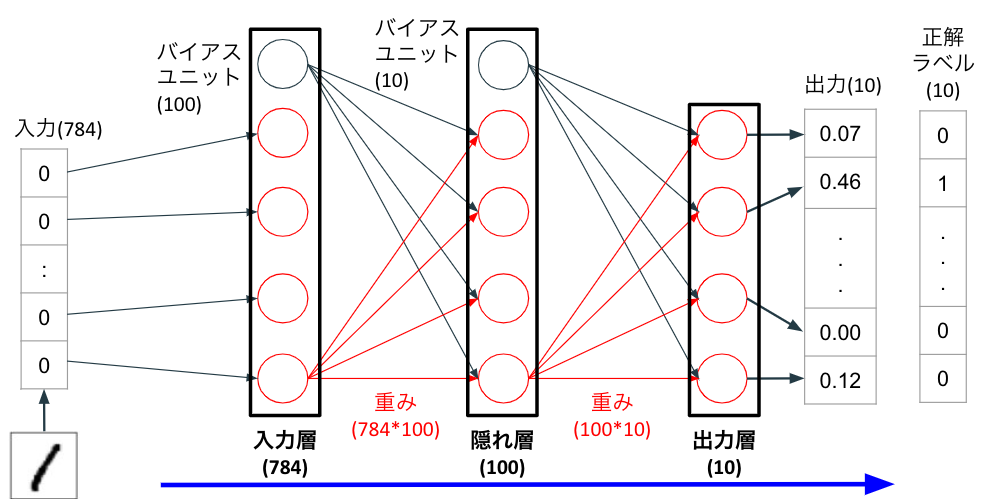
-
画像データの一次元配列を入力値として、入力層に受け渡す。
-
配列の各要素に重みをかけて、隠れ層の各ニューロンに受け渡す。全ての値の総和にバイアスを加える。
1番目の入力層から1番目の隠れ層にかかる重みを$w_{1,1}^{(h)}$,1番目の隠れ層の入力の総和を$z_1^{(h)}$,そこに加えるバイアスを$b_1^{(h)}$とする。
$$z_1^{(h)}=w_{1,1}^{(h)}x_1+...+w_{784,100}^{(h)}x_{784}+b_1^{(h)}$$ -
隠れ層の各ニューロンの$z^{(h)}$を活性化関数に代入する。1番目の隠れ層の活性化関数の出力値を$a_1^{(h)}$とする。
$\exp(z)$は$e^{z}$と同義である。
$$a_1^{(h)}=\frac{1}{1+\exp(z_1^{(h)})}$$
-
隠れ層の各出力値$a^{(h)}$に重みをかけて、出力層の各ニューロンに受け渡す。全ての値の総和にバイアスを加える。
1番目の隠れ層から1番目の出力層にかかる重みを$w_{1,1}^{(out)}$,1番目の隠れ層の入力の総和を$z_1^{(out)}$,そこに加えるバイアスを$b_1^{(out)}$とする。
$$z_1^{(out)}=w_{1,1}^{(out)}a_1^{(h)}+...+w_{100,10}^{(out)}a_{10}^{(h)}+b_1^{(out)}$$ -
出力層の各ニューロンの$z^{(out)}$を活性化関数に代入する。1番目の出力層の活性化関数の出力値を$a_1^{(out)}$とする。
$$a_1^{(out)}=\frac{1}{1+\exp(z_1^{(out)})}$$
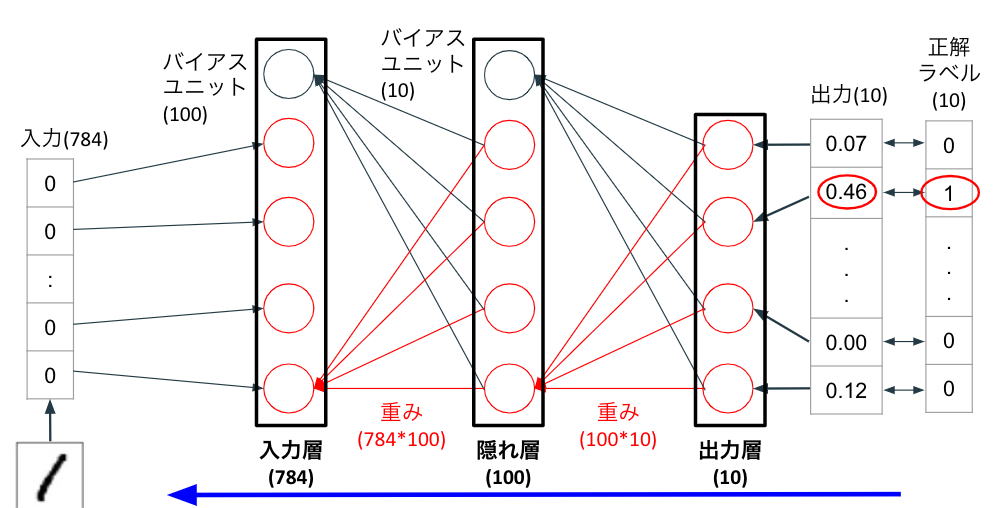
- 最終的に得られた出力値: $a_1^{out}$は画像に書かれた数字が0であると認識される確率を表します。上図の例では0.07がそれにあたります。すなわち、出力層の各ニューロンからの出力値は0から9に分類される確率を示しており、最も高い値が配列の要素として含まれる要素番号が分類される数字になります。
しかし、このままでは1と認識する確率が46%しかないので決して精度が高いとは言えません。理想は要素番号2のみ1となって、それ以外の要素は0になることです。正解が一致するためには重みとバイアスを修正しなければなりません。次項目では重みとバイアスを更新する手順について見ていきます。
逆伝播
ニューラルネットワークがどのようにして、重みとバイアスを更新するのかを見ていくために逆伝播:バックプロパゲーションについて解説します。数式の意味や導出は次項目で詳しく解説しますので、本項目では流れを抑えていただくだけで十分です。
ニューロンひとつあたりの重みとバイアスの更新
-
出力層の出力値$a_1^{(out)}$と正解ラベル$y_1$の値との誤差$\delta_1^{(out)}$は下記のように求められます。
$$\delta_1^{(out)}=a_1^{(out)}-y_1$$ -
出力層の重みの勾配$grad^{(w_{1,1}^{(out)})}$は下記のように求められます。
$$grad^{(w_{1,1}^{(out)})}={a_1^{(h)}}\delta_1^{(out)}$$ -
出力層のバイアスの勾配$grad^{(w_{1,1}^{(out)})}$は下記のように求められます。
$$grad^{(b_{1}^{(out)})}=\delta_1^{(out)}$$ -
勾配をもとに重みは下記のように更新されます。$\eta$は学習率、$l_2$はL2正則化の係数を表します。
$$w_{1,1}^{(out)}=w_{1,1}^{(out)}-\eta(grad^{(w_{1,1}^{(out)})}+l_2w_{1,1}^{(out)})$$ -
また勾配をもとにバイアスは下記のように更新されます。
$$b_{1}^{(out)}=b_{1}^{(out)}-\eta grad^{(b_{1}^{(out)})}$$
入力層から隠れ層の重みとバイアスの更新も上記の手順と同様に進めますが、式が複雑なため次項目で解説します。
重みとバイアスの更新
よりわかりやすく解説するために、入力層には1つ、隠れ層には2つ、出力層には1つのニューロンを持つニューラルネットワークを用います。w1(o1)は隠れ層のニューロンh1から出力層のニューロンo1にかかる重みを表しています。以降の解説では$w_{1,1}^{(out)}$と表記します。
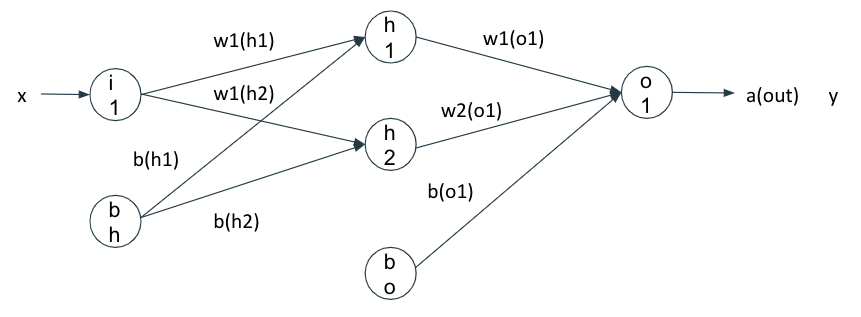
結論から言うと、コスト関数を更新したいパラメータで連鎖律を使った偏微分をすることで更新できます。
$$
J(W)=- \bigl[\sum_{i=1}^{n}\sum_{j=1}^{t} y_j^{[i]}\log(a_j^{[i]})+(1-y_j^{[i]})\log(1-a_j^{[i]})\bigr]+\frac{\lambda}{2}\sum_{l=1}^{L-1}\sum_{i=1}^{u_l}\sum_{j=1}^{u_l+1}(w_{j,i}^{(l)})^2
$$
出力層から中間層
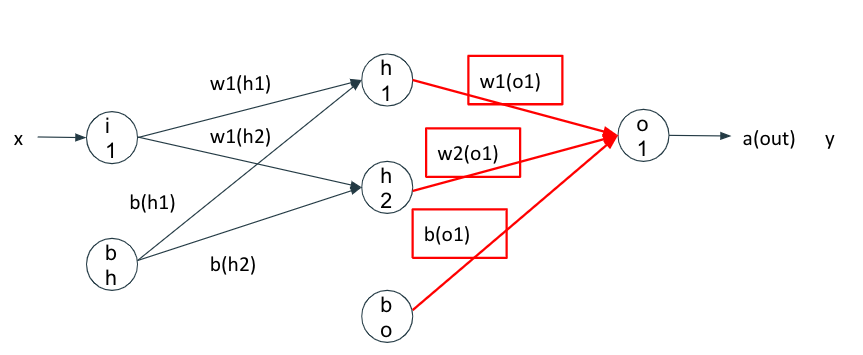
$$w_{1,1}^{(out)}=w_{1,1}^{(out)}-\eta \frac{\partial J(W)}{\partial w_{1,1}^{(out)}}・・・(1)$$
$$w_{2,1}^{(out)}=w_{2,1}^{(out)}-\eta \frac{\partial J(W)}{\partial w_{2,1}^{(out)}}・・・(2)$$
$$b_{1}^{(out)}=b_{1}^{(out)}-\eta \frac{\partial J(W)}{\partial b_{1}^{(out)}}・・・(3)$$
$$a^{(out)}=\frac{1}{1+\exp(-z^{(out)})}, $$
$$z^{(out)}=w_{1,1}^{(out)}a_{1}^{(h)}+w_{1,1}^{(out)}a_{1}^{(h)}+b_{1}^{(out)}$$
(1)について、$J(W)$を$w_{1,1}^{(out)}$で連鎖律を使った偏微分をすればいいので
$$\frac{\partial J(W)}{\partial w_{1,1}^{(out)}}=\frac{\partial J(W)}{\partial a^{(out)}}・\frac{\partial a^{(out)}}{\partial z^{(out)}}・\frac{\partial z^{(out)}}{\partial w_{1,1}^{(out)}}=-\bigl[y・\frac{1}{a^{(out)}}+(1-y)・\frac{-1}{1-a^{(out)}}\bigr]・a^{(out)}(1-a^{(out)})・a_{1}^{(h)}+\lambda w_{1,1}^{(out)}$$$$=(a^{(out)}-y)・a_{1}^{(h)}+\lambda w_{1,1}^{(out)}$$
$$w_{1,1}^{(out)}=w_{1,1}^{(out)}-\eta ((a^{(out)}-y)・a_{1}^{(h)}+\lambda w_{1,1}^{(out)})$$
(2)について、$J(W)$を$w_{2,1}^{(out)}$も同様に計算して
$$\frac{\partial J(W)}{\partial w_{2,1}^{(out)}}=(a^{(out)}-y)・a_{2}^{(h)}+\lambda w_{2,1}^{(out)}$$
$$w_{2,1}^{(out)}=w_{2,1}^{(out)}-\eta ((a^{(out)}-y)・a_{2}^{(h)}+\lambda w_{2,1}^{(out)})$$
(3)について、$J(W)$を$b_{1}^{(out)}$で連鎖律を使った偏微分をすればいいので
$$\frac{\partial J(W)}{\partial b_{1}^{(out)}}=\frac{\partial J(W)}{\partial a^{(out)}}・\frac{\partial a^{(out)}}{\partial z^{(out)}}・\frac{\partial z^{(out)}}{\partial b_{1}^{(out)}}=(a^{(out)}-y)・1=a^{(out)}-y$$
$$b_{1}^{(out)}=b_{1}^{(out)}-\eta(a^{(out)}-y)$$
中間層から入力層
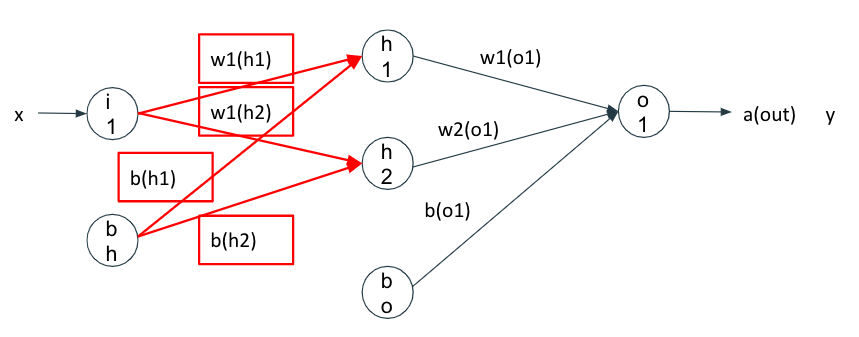
$$w_{1,1}^{(h)}=w_{1,1}^{(h)}-\eta \frac{\partial J(W)}{\partial w_{1,1}^{(h)}}・・・(1)'$$
$$w_{1,2}^{(h)}=w_{1,2}^{(h)}-\eta \frac{\partial J(W)}{\partial w_{1,2}^{(h)}}・・・(2)'$$
$$b_{1}^{(h)}=b_{1}^{(h)}-\eta \frac{\partial J(W)}{\partial b_{1}^{(h)}}・・・(3)'$$
$$b_{2}^{(h)}=b_{2}^{(h)}-\eta \frac{\partial J(W)}{\partial b_{2}^{(h)}}・・・(4)'$$
$$a_{1}^{(h)}=\frac{1}{1+\exp(-z_{1}^{(h)})},a_{2}^{(h)}=\frac{1}{1+\exp(-z_{2}^{(h)})}$$
$$z_1^{(h)}=w_{1,1}^{(h)}x+b_{1}^{(h)},z_2^{(h)}=w_{1,2}^{(h)}x+b_{2}^{(h)}$$
$(1)'$について、$J(W)$を$w_{1,1}^{(h)}$で連鎖律を使った偏微分をすればいいので
$$\frac{\partial J(W)}{\partial w_{1,1}^{(h)}}=\frac{\partial J(W)}{\partial a^{(out)}}・\frac{\partial a^{(out)}}{\partial z^{(out)}}・\frac{\partial z^{(out)}}{\partial a_{1}^{(h)}}・\frac{\partial a_{1}^{(h)}}{\partial z_{1}^{(h)}}・\frac{\partial z_{1}^{(h)}}{\partial w_{1,1}^{(h)}}$$
$$=(a^{(out)}-y)・w_{1,1}^{(out)}・a_{1}^{(h)}・(1-a_1^{(h)})・x+\lambda w_{1,1}^{(h)}$$
$$w_{1,1}^{(h)}=w_{1,1}^{(h)}-\eta ((a^{(out)}-y)・w_{1,1}^{(out)}・a_{1}^{(h)}・(1-a_1^{(h)})・x+\lambda w_{1,1}^{(h)})$$
$(2)'$について、$J(W)$を$w_{1,2}^{(h)}$も同様に計算して
$$\frac{\partial J(W)}{\partial w_{1,2}^{(h)}}=\frac{\partial J(W)}{\partial a^{(out)}}・\frac{\partial a^{(out)}}{\partial z^{(out)}}・\frac{\partial z^{(out)}}{\partial a_{2}^{(h)}}・\frac{\partial a_{2}^{(h)}}{\partial z_{2}^{(h)}}・\frac{\partial z_{2}^{(h)}}{\partial w_{1,2}^{(h)}}$$
$$=(a^{(out)}-y)・w_{2,1}^{(out)}・a_{2}^{(h)}・(1-a_2^{(h)})・x+\lambda w_{1,2}^{(h)}$$
$$w_{1,2}^{(h)}=w_{1,2}^{(h)}-\eta ((a^{(out)}-y)・w_{2,1}^{(out)}・a_{2}^{(h)}・(1-a_2^{(h)})・x+\lambda w_{1,2}^{(h)})$$
$(3)'$について、$J(W)$を$b_{1}^{(h)}$で連鎖律を使った偏微分をすればいいので
$$\frac{\partial J(W)}{\partial b_{1}^{(h)}}=\frac{\partial J(W)}{\partial a^{(out)}}・\frac{\partial a^{(out)}}{\partial z^{(out)}}・\frac{\partial z^{(out)}}{\partial a_{1}^{(h)}}・\frac{\partial a_{1}^{(h)}}{\partial z_{1}^{(h)}}・\frac{\partial z_{1}^{(h)}}{\partial b_{1}^{(h)}}$$
$$=(a^{(out)}-y)・w_{1,1}^{(out)}・a_{1}^{(h)}・(1-a_1^{(h)})$$
$$b_{1}^{(h)}=b_{1}^{(h)}-\eta ((a^{(out)}-y)・w_{1,1}^{(out)}・a_{1}^{(h)}・(1-a_1^{(h)})$$
$(4)'$について、$J(W)$を$b_{2}^{(h)}$で連鎖律を使った偏微分をすればいいので
$$\frac{\partial J(W)}{\partial w_{1,2}^{(h)}}=\frac{\partial J(W)}{\partial a^{(out)}}・\frac{\partial a^{(out)}}{\partial z^{(out)}}・\frac{\partial z^{(out)}}{\partial a_{2}^{(h)}}・\frac{\partial a_{2}^{(h)}}{\partial z_{2}^{(h)}}・\frac{\partial z_{2}^{(h)}}{\partial w_{1,2}^{(h)}}$$
$$=(a^{(out)}-y)・w_{2,1}^{(out)}・a_{2}^{(h)}・(1-a_2^{(h)})$$
$$b_{2}^{(h)}=b_{2}^{(h)}-\eta ((a^{(out)}-y)・w_{2,1}^{(out)}・a_{2}^{(h)}・(1-a_2^{(h)})$$
このように1つ前の層から得られた計算結果をもとに、さらに1つ前の層に誤差を伝播させているので誤差逆伝播法と呼ばれています。また偏微分をするので、活性化関数は微分可能な関数である必要があります。
実装
1.データの読み込み
外部より画像データを読み込みます。
import sys
import gzip
import shutil
import os
if (sys.version_info > (3, 0)):
writemode = 'wb'
else:
writemode = 'w'
zipped_mnist = [f for f in os.listdir() if f.endswith('ubyte.gz')]
for z in zipped_mnist:
with gzip.GzipFile(z, mode='rb') as decompressed, open(z[:-3], writemode) as outfile:
outfile.write(decompressed.read())
def load_mnist(path, kind='train'):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte' % kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte' % kind)
with open(labels_path, 'rb') as lbpath:
magic, n = struct.unpack('>II',
lbpath.read(8))
labels = np.fromfile(lbpath,
dtype=np.uint8)
with open(images_path, 'rb') as imgpath:
magic, num, rows, cols = struct.unpack(">IIII",
imgpath.read(16))
images = np.fromfile(imgpath,
dtype=np.uint8).reshape(len(labels), 784)
images = ((images / 255.) - .5) * 2
return images, labels
2.ニューラルネットワークの構築
import numpy as np
import sys
class NeuralNetMLP(object):
""" Feedforward neural network / Multi-layer perceptron classifier.
Parameters
------------
n_hidden : int (default: 30)
Number of hidden units. 中間層(隠れ層)の数
l2 : float (default: 0.)
Lambda value for L2-regularization.
No regularization if l2=0. (default) L2正則化の係数
epochs : int (default: 100)
Number of passes over the training set. エポック数、何回学習するか
eta : float (default: 0.001)
Learning rate. 学習率
shuffle : bool (default: True)
Shuffles training data every epoch if True to prevent circles. エポックごとに扱う学習データをシャッフル
minibatch_size : int (default: 1)
Number of training examples per minibatch. 1ミニバッジあたりの学習データのサイズ
seed : int (default: None)
Random seed for initializing weights and shuffling. 乱数生成のシード
Attributes
-----------
eval_ : dict
Dictionary collecting the cost, training accuracy,
and validation accuracy for each epoch during training. 評価指標:コスト、正確性、各エポックごとの検証を行ったときの正確性
"""
#初期メソッド----------------------------------------------------------<
def __init__(self, n_hidden=20,
l2=0., epochs=200, eta=0.001,
shuffle=True, minibatch_size=1, seed=None):
self.random = np.random.RandomState(seed)
self.n_hidden = n_hidden
self.l2 = l2
self.epochs = epochs
self.eta = eta
self.shuffle = shuffle
self.minibatch_size = minibatch_size
#ワンホットエンコーディングするメソッド----------------------------------------------------------<
def _onehot(self, y, n_classes):
"""Encode labels into one-hot representation
Parameters
------------
y : array, shape = [n_examples]
Target values. 目的変数:文字が何の数字を表しているかのラベル
n_classes : int
Number of classes 分類されるクラスの数
Returns
-----------
onehot : array, shape = (n_examples, n_labels): 60000(データの数)*10(0-9のラベルの数)
ラベルが0のとき、0の列には1/残りの1-9の列には0
"""
onehot = np.zeros((n_classes, y.shape[0]))
for idx, val in enumerate(y.astype(int)):
onehot[val, idx] = 1.
return onehot.T
#活性化関数のシグモイド関数----------------------------------------------------------<
def _sigmoid(self, z):
"""Compute logistic function (sigmoid)
zの値が最小値:-250,最大値:250の範囲に収まるように指定
"""
return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
#フォワードプロパゲーション(順伝播法)----------------------------------------------------------<
def _forward(self, X):
"""Compute forward propagation step
引数:説明変数(画像データを一次元配列に変換したデータ,サイズは784)
戻り値:隠れ層の総入力・活性化関数、出力層の総入力・活性化関数
"""
# step 1: net input of hidden layer(入力層から中間層)#
# [n_examples, n_features] dot [n_features, n_hidden]
# -> [n_examples, n_hidden]
#(60000,784)*(784,100)->(60000,100), そこに各伝達経路の重みベクトル(サイズ=中間層の数:100)を足している
z_h = np.dot(X, self.w_h) + self.b_h
# step 2: activation of hidden layer#
#z_hをシグモイド関数に渡して0.0より大きく1.0より小さい値を得る
a_h = self._sigmoid(z_h)
# step 3: net input of output layer(中間層から出力層)#
# [n_examples, n_hidden] dot [n_hidden, n_classlabels]
# -> [n_examples, n_classlabels]
#(60000,100)*(100,10)->(60000,10), そこに各伝達経路の重みベクトル(サイズ=中間層の数:100)を足している
z_out = np.dot(a_h, self.w_out) + self.b_out
# step 4: activation output layer
a_out = self._sigmoid(z_out)
return z_h, a_h, z_out, a_out
#コスト関数の値を計算して返すメソッド----------------------------------------------------------<
def _compute_cost(self, y_enc, output):
"""Compute cost function.
Parameters
----------
y_enc : array, shape = (n_examples, n_labels)
one-hot encoded class labels.
ワンホットエンコーディングした正解ラベル
output : array, shape = [n_examples, n_output_units]
Activation of the output layer (forward propagation)
出力層の出力値(予測値)
Returns
---------
cost : float
Regularized cost
損失関数と罰則項の合計
"""
L2_term = (self.l2 *
(np.sum(self.w_h ** 2.) +
np.sum(self.w_out ** 2.)))
term1 = -y_enc * (np.log(output))
term2 = (1. - y_enc) * np.log(1. - output)
cost = np.sum(term1 - term2) + L2_term
return cost
# If you are applying this cost function to other
# datasets where activation
# values maybe become more extreme (closer to zero or 1)
# you may encounter "ZeroDivisionError"s due to numerical
# instabilities in Python & NumPy for the current implementation.
# I.e., the code tries to evaluate log(0), which is undefined.
# To address this issue, you could add a small constant to the
# activation values that are passed to the log function.
#
# For example:
#
# term1 = -y_enc * (np.log(output + 1e-5))
# term2 = (1. - y_enc) * np.log(1. - output + 1e-5)
#return cost
#分類クラスを予測するメソッド----------------------------------------------------------<
def predict(self, X):
"""Predict class labels
Parameters
-----------
X : array, shape = [n_examples, n_features]
Input layer with original features.
Returns:
----------
y_pred : array, shape = [n_examples]
Predicted class labels.
"""
z_h, a_h, z_out, a_out = self._forward(X)
y_pred = np.argmax(z_out, axis=1)
return y_pred
#データを渡してfitさせるメソッド----------------------------------------------------------<
def fit(self, X_train, y_train, X_valid, y_valid):
""" Learn weights from training data.
Parameters
-----------
X_train : array, shape = [n_examples, n_features]
Input layer with original features.
訓練データの入力値
y_train : array, shape = [n_examples]
Target class labels.
訓練データの正解ラベル
X_valid : array, shape = [n_examples, n_features]
Sample features for validation during training
検証データの入力値
y_valid : array, shape = [n_examples]
Sample labels for validation during training
検証データの正解ラベル
Returns:
----------
self
"""
#出力値(分類クラス)の数=10
n_output = np.unique(y_train).shape[0] # number of class labels
#特徴量の数=784
n_features = X_train.shape[1]
########################
# Weight initialization
########################
# weights for input -> hidden
#入力層から隠れ層の伝達経路の重みとバイアス、0で初期化
self.b_h = np.zeros(self.n_hidden)
self.w_h = self.random.normal(loc=0.0, scale=0.1,
size=(n_features, self.n_hidden))
# weights for hidden -> output
#隠れ層から出力層の伝達経路の重みとバイアス、0で初期化
self.b_out = np.zeros(n_output)
self.w_out = self.random.normal(loc=0.0, scale=0.1,
size=(self.n_hidden, n_output))
#エポック数をログ表示させるために桁数を格納
epoch_strlen = len(str(self.epochs)) # for progress formatting
#コスト関数の戻り値、訓練データと検証データの正答率をログ表示
self.eval_ = {'cost': [], 'train_acc': [], 'valid_acc': []}
#追加------<
#self.cost_function=[]
#訓練データの分類ラベルをワンホットエンコーディング
y_train_enc = self._onehot(y_train, n_output)
# iterate over training epochs
#指定したエポック数分だけ学習させる
for i in range(self.epochs):
# iterate over minibatches
#全てのデータをバッチサイズいくつで分割するかで学習する回数が決まる
#バッチごとに学習して予測
#全てのバッチ、すなわち全データの予測が終了して初めて1エポックとなる
indices = np.arange(X_train.shape[0])
if self.shuffle:
self.random.shuffle(indices)
for start_idx in range(0, indices.shape[0] - self.minibatch_size +
1, self.minibatch_size):
batch_idx = indices[start_idx:start_idx + self.minibatch_size]
# forward propagation
z_h, a_h, z_out, a_out = self._forward(X_train[batch_idx])
##################
# Backpropagation
##################
# [n_examples, n_classlabels]
#予測と正解の誤差:出力層の誤差項
delta_out = a_out - y_train_enc[batch_idx]
# [n_examples, n_hidden]
#隠れ層の出力値(シグモイド関数)を総入力で微分
sigmoid_derivative_h = a_h * (1. - a_h)
# [n_examples, n_classlabels] dot [n_classlabels, n_hidden]
# -> [n_examples, n_hidden]
#隠れ層の誤差項
delta_h = (np.dot(delta_out, self.w_out.T) *
sigmoid_derivative_h)
# [n_features, n_examples] dot [n_examples, n_hidden]
# -> [n_features, n_hidden]
#隠れ層の重みとバイアスの勾配
grad_w_h = np.dot(X_train[batch_idx].T, delta_h)
grad_b_h = np.sum(delta_h, axis=0)
# [n_hidden, n_examples] dot [n_examples, n_classlabels]
# -> [n_hidden, n_classlabels]
#出力層の重みとバイアスの勾配
grad_w_out = np.dot(a_h.T, delta_out)
grad_b_out = np.sum(delta_out, axis=0)
# Regularization and weight updates
#隠れ層の誤差項より重み・バイアスを更新
delta_w_h = (grad_w_h + self.l2*self.w_h)
delta_b_h = grad_b_h # bias is not regularized
self.w_h -= self.eta * delta_w_h
self.b_h -= self.eta * delta_b_h
#出力層の誤差項より重み・バイアスを更新
delta_w_out = (grad_w_out + self.l2*self.w_out)
delta_b_out = grad_b_out # bias is not regularized
self.w_out -= self.eta * delta_w_out
self.b_out -= self.eta * delta_b_out
#############
# Evaluation
#############
# Evaluation after each epoch during training
#エポックごとに結果を格納して精度を表示させる
z_h, a_h, z_out, a_out = self._forward(X_train)
cost = self._compute_cost(y_enc=y_train_enc,
output=a_out)
#追加-----------<
#self.cost_function.append(cost)
y_train_pred = self.predict(X_train)
y_valid_pred = self.predict(X_valid)
train_acc = ((np.sum(y_train == y_train_pred)).astype(np.float) /
X_train.shape[0])
valid_acc = ((np.sum(y_valid == y_valid_pred)).astype(np.float) /
X_valid.shape[0])
#ログの表示
sys.stderr.write('\r%0*d/%d | Cost: %.2f '
'| Train/Valid Acc.: %.2f%%/%.2f%% ' %
(epoch_strlen, i+1, self.epochs, cost,
train_acc*100, valid_acc*100))
sys.stderr.flush()
#print(self.eval_['cost'])
self.eval_['cost'].append(cost)
self.eval_['train_acc'].append(train_acc)
self.eval_['valid_acc'].append(valid_acc)
return self
3.データを渡して学習・予測
"""
ニューラルネットワークの学習と予測を行う関数
引数:なし
戻り値:なし
学習のログ、実行時間
モデルを使った予測結果
"""
import time
def learn_pred():
#ニューラルネットワークにパラメータを渡す
nn = NeuralNetMLP(n_hidden=100,
l2=0.01,
epochs=100,
eta=0.0005,
minibatch_size=100,
shuffle=True,
seed=1)
s=time.time()
#訓練データ:60000→学習用:55000, 検証用:5000
nn.fit(X_train=X_train[:55000],
y_train=y_train[:55000],
X_valid=X_train[55000:],
y_valid=y_train[55000:])
e=time.time()
#テストデータ:10000を予測
y_test_pred = nn.predict(X_test)
acc = (np.sum(y_test == y_test_pred).astype(np.float) / X_test.shape[0])
cost_function=nn.eval_['cost']
#結果の出力
print('テストデータの正答率: %.2f%%' % (acc * 100))
print(f'実行時間: {e-s}秒')
return cost_function
4.実行結果
テストデータの正答率: 97.16%
実行時間: 233.2243790626526秒
5.誤認識したデータの確認
miscl_img = X_test[y_test != y_test_pred][:25]
correct_lab = y_test[y_test != y_test_pred][:25]
miscl_lab = y_test_pred[y_test != y_test_pred][:25]
fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(25):
img = miscl_img[i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_title('%d) t: %d p: %d' % (i+1, correct_lab[i], miscl_lab[i]))
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.savefig('12_09.png', dpi=300)
plt.show()
まとめ
ニューラルネットワークを勉強してみて、とにかく微分などの数学の知識が必要な内容だと感じました。これからニューラルネットワークを勉強する方は数学の勉強もすることをオススメします。今回は隠れ層が1つで実装しましたが、この層が多くなると深層学習(ディープラーニング)の実装になり、より複雑な画像の認識ができるのでチャレンジしてみたいです。大の坂道グループ好きな私は、すぐに推しメンの画像を見つけ出せる画像認識システムを作りたいと感じました。
参考資料
- 書籍: Python機械学習プログラミング
- Udemy: みんなのAI講座