マハラノビス距離に基づく異常値検知について説明をします.
実装編はこちら
これは,教師なし学習により,データのパタンを学習し,このデータから著しく外れたデータを異常値として検出する方法です.
マハラノビス距離とは,統計学で用いられる距離を表す手法の1つです.
似た距離の表す手法としてユークリッド距離がありますね.
おさらい
まずはじめにユークリッド距離の説明をしておさらいをしたいと思います.
ユークリッド距離とは,いわゆる「一般的」な距離を表す手法です.
ピタゴラスの定理で求められることはご存知だと思います.
簡単に2次元平面で考えると,
{ \displaystyle
p = (p_1,p_2)
}
および,
{ \displaystyle
q = (q_1,q_2)
}
のとき,それらの距離は
{ \displaystyle
d(p,q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2}
}
で求められますね.
これが一般的な距離計算の手法です.
マハラノビス距離
マハラノビス距離は,先程も説明したように,統計学で用いられる距離を表す手法の1つです.
どういうタイミングで用いられるかというと,多次元のデータが相関を持つ場合に使用される機会が多いです.
仮に,データがn次元の連続ベクトルであるとして,得られたデータ列を,
x^m = x_1,x_2,…x_m
(これらは全てベクトルの集合と考えて下さい)として,
i番目のデータは,
{
x_i = \left(
\begin{array}{c}
x_i,_1 \\
x_i,_2 \\
\vdots \\
x_i,_n
\end{array}
\right)
}
と記すとき,その平均値ベクトル
μ
,分散共分散行列
\sum_{}
は以下のように求められます.
平均値ベクトル
{
μ = \frac{1}{m} \sum_{i=1}^m x_i
}
分散共分散行列
\sum_{} = \frac{1}{m}\sum_{i=1}^m (x_i - μ)(x_i - μ)^{\mathrm{T}}
そこで,θをしきい値パラメータとして,新しいデータxに対して,
θ < \sqrt{(x_i - μ) ^{\mathrm{T}}\sum{}^{-1} (x_i - μ) }
を満たすならば,xは異常値であると判定します.
この式の右辺がマハラノビス距離と呼ばれるものです.
もっとマハラノビス距離
ここで,
\sum_{}
が単位行列であるときは,ユークリッド距離の2乗が求まります.
対角行列であるときには,次元ごとのスケールが異なります.
非対角行列であるときは,これにさらに回転が加わることになります.
下記に示すのは,2次元ベクトル上でのマハラノビス距離に基づく外れ値検出のイメージ図です.
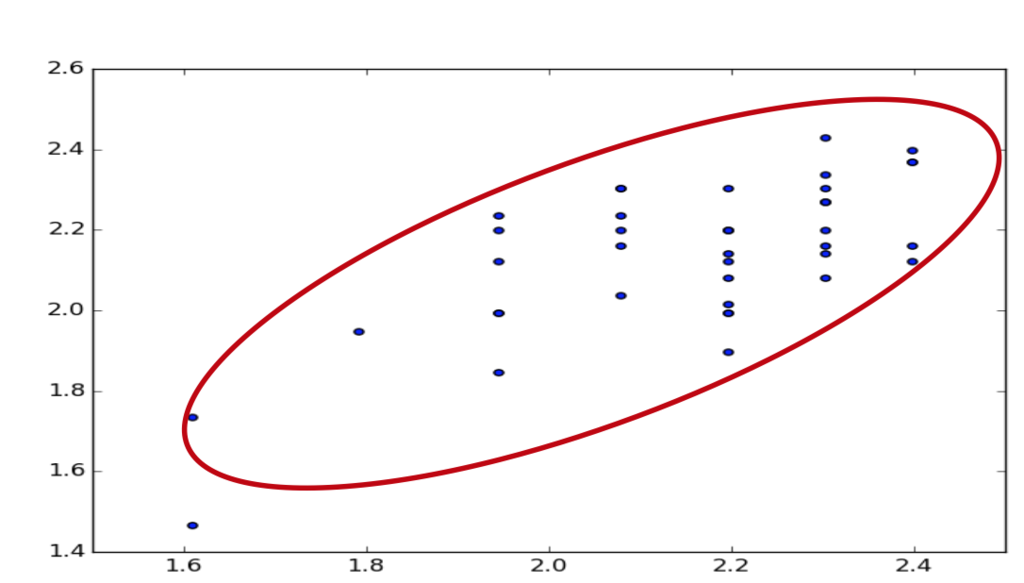
これは,プロットされた点が,データ点であり,そのデータ点を覆うように楕円が表示されています.
この楕円の中に含まれていない点が外れ値になります.
したがって,閾値θは,この楕円の大きさを示すものであり,どの程度許すかによって外れ値の割合が変化してきます.
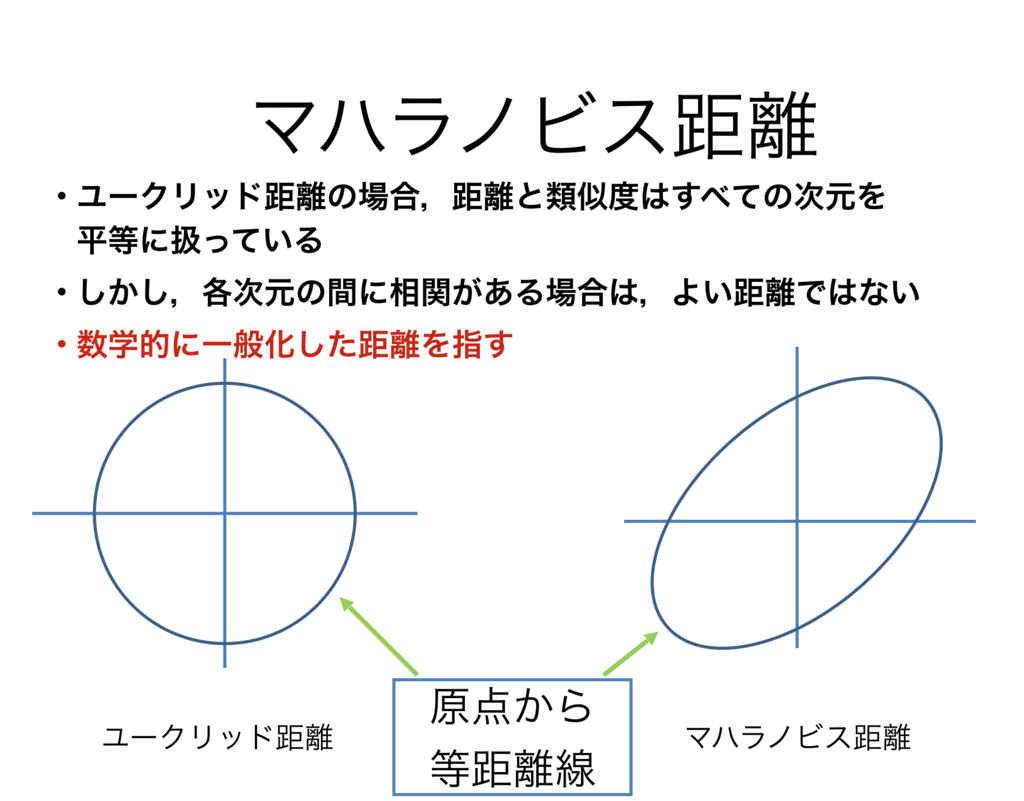
ユークリッド距離とマハラノビス距離の違い
この図を見てもらうのが分かりやすいです.
ユークリッド距離とマハラノビス距離の違いは,距離を定義する際に,多次元のデータの相関を考慮しているかいないかという点にあります.
マハラノビス距離において,相関が強い距離の方向とは,実際の距離よりも相対的に短くなるという考え方です.
ユークリッド距離の場合,距離はx軸,y軸ともに等しい距離になります.
しかしマハラノビス距離は,x軸,y軸ともに分散で形が定まっています.
つまり,分散が大きいと,原点からの距離はあまり離れていないと解釈することができますし,
分散が小さいと,原点からの距離は大きく離れているということになります.
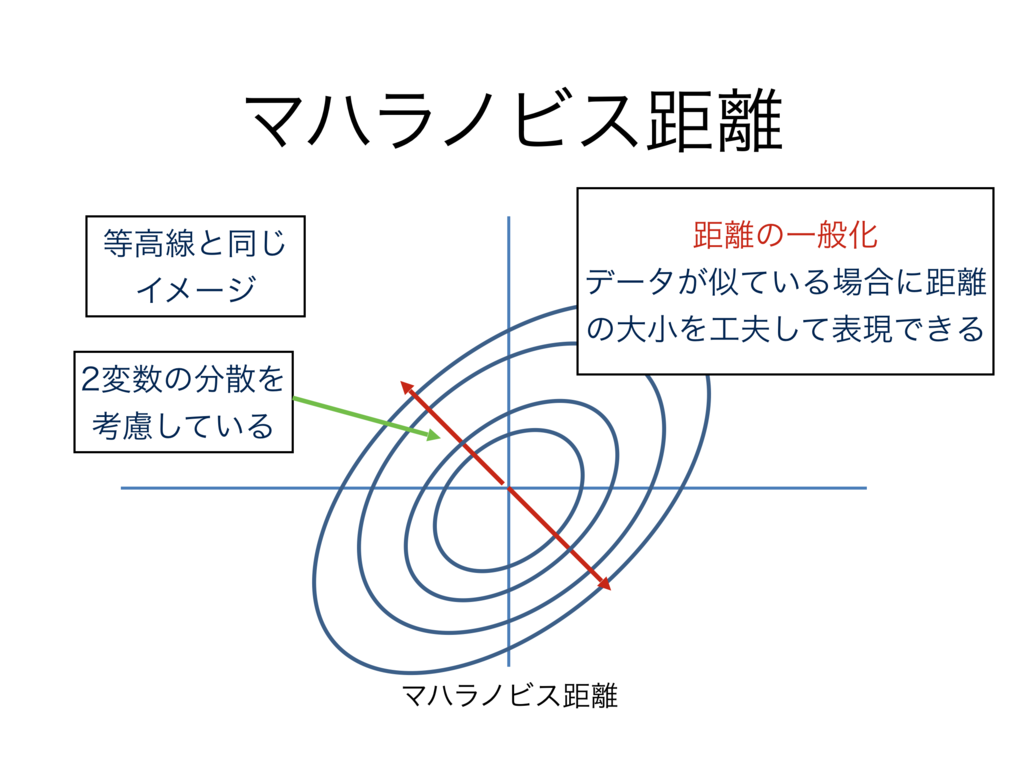
もう少し詳しくマハラノビス距離
この図は,原点から楕円が複数にわたって描かれています.
この楕円の大きさが,異常値の閾値の大きさを示しています.
閾値が大きいと楕円が大きく,異常値の割合は少なくなります.
楕円の形は分散によって決まるという話をしましたが,この図を山の等高線のようなイメージで解釈してもらっても結構です.
等高線は,同じ高さにある山の部分をくくっています.
マハラノビス距離も同じです.
軸という概念を考えずに,同じ楕円で囲まれた範囲のものが閾値の値になっているという解釈をすれば,円の歪み方にも納得がいくのではないかと思います.
マハラノビス距離の問題点
マハラノビス距離による異常値検出の手法では,平均値ベクトルと分数といった基本概念を通じて異常値の概念を定式化しています.
しかし,平均値自身は,異常値の影響を大きくウケるため,中央値の考え方を利用して異常値検出を行う方法も提案されていたりします.(ここでは割愛)
また,個人的に重要なのは,このマハラノビス距離を用いた距離計算手法では,boolean値のみのデータは使えません.
(1 or 0 の平均値から,1 or 0の論理値を引いて… という手法になるので,何が起きるかは考えてみてください…)
まとめ
- マハラノビス距離は,距離を一般化したものである.
- マハラノビス距離は,各次元における相関を考慮した距離である.
次回は実装編ということでpythonで実際に実装を行ってみます.