More than 5 years have passed since last update.

教師なし学習による異常値検知: マハラノビス距離 (実装編)

Last updated at 2015-10-01Posted at 2015-10-01

さて，前回の理論編の続きということで，今回は実際にマハラノビス距離をpythonで実装しようと思います．
前回の理論編はこちらからどうぞ
教師なし学習による異常値検知: マハラノビス距離 (理論編)

はじめに

Pythonのscikit-learnというライブラリでは，マハラノビス距離を計算する関数が実装されています．
Robust covariance estimation and Mahalanobis distances relevance

ただ，このコードを実行します! という記事を書いてもただの英訳になってしまうので，
今回は自分で実装し，計算過程がプログラム上ではどうなっているのかを見ていきます．

最終的に全てのコードをつなぎ合わせたら，自分で距離計算が出来るというところまでを目標にします．

環境

Mac OSX Mavericks
Python3系列(3.4)

また，今回の実験で扱うファイルは以下の様な形式だとします．
Columnがマシンの番号，Rowはマシンのスコアだとします．
(逆でも良いでしょというイチャモンが飛んできそうですがもちろん逆でも問題ないです．)

test.csv

	1	2	3	4	5	6	7	8	9	10
a	0	6	7	2	3	3	1	0	0	1
b	1	1	11	6	0	2	1	4	1	2
c	2	12	32	5	0	1	3	4	1	1
d	3	3	7	3	2	2	2	1	2	5
e	4	6	6	3	5	1	1	1	1	3
f	5	7	9	5	0	2	2	1	1	2

この形式だと，マシン番号3番目だけ，やたらとスコアが高そうですね．

マハラノビス距離では，あるしきい値を自分自身で設定し，しきい値を超えた値のあるレコードを異常値としてを判定する事が出来ます．
注意ですが，しきい値はその都度自分自身で設定する必要があります．
今回は，こちら側でしきい値を設けずにグラフとして図示することで異常なデータの可視化を行います．

実装

import

importする関数は以下のようになります．

numpy
scipy
pandas
matplotlib
pylab

これらのインストール手順などは，今回は割愛します．
インストールについては，基本的にはpipやeasy_installなどを用いるのが良いです．

# -*- coding: utf-8 -*-
import numpy as np
import scipy as sc
from scipy import linalg
from scipy import spatial
import scipy.spatial.distance
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.font_manager
import pylab

変数定義

今回は，ROWが6行，COLUMNが10行あるので以下のように定義します．
また，先ほどのtest.csvを読み込むのでこちらも読み込んでおきます．

ROW = 10
COLUMN = 6
csv = pd.read_csv('test.csv')

同時に今後扱う変数も先にこちらで定義しておきます．

# row:行,column:列,ave:平均,vcm:分散共分散行列
row = []
column = []
ave = [0.0 for i in range(ROW)]
vcm = np.zeros((COLUMN, ROW, ROW))
diff = np.zeros((1, ROW))
mahal = np.zeros(COLUMN)
tmp = np.zeros(ROW)

欠損値削除

一般的なデータでは，このような test.csvのように全てのデータが埋め尽くされているケースはあまり多くないです．
私は，このような時には，以下のようにして欠損値の削除をしてしまいます．

# data欠損値の削除
# axis = 1 で，欠損値のある列を削除
trans_data = csv.dropna(axis=1)
print(trans_data)

これをprintすると，

  Unnamed: 0  1   2   3  4  5  6  7  8  9  10
0          a  0   6   7  2  3  3  1  0  0   1
1          b  1   1  11  6  0  2  1  4  1   2
2          c  2  12  32  5  0  1  3  4  1   1
3          d  3   3   7  3  2  2  2  1  2   5
4          e  4   6   6  3  5  1  1  1  1   3
5          f  5   7   9  5  0  2  2  1  1   2

こんな感じで出力されます．

また，このようにして整形したデータをlist形式にして，先ほど宣言したrow,columnに格納していきます．

# rowにtrans_dataの要素をリストの形式で連結
for i in range(ROW):
    row.append(list(trans_data.ix[i]))
print(row)

# 列を連結
for i in range(1, COLUMN+1):
    column.append(list(trans_data.ix[:, i]))
print(column)

#rowの計算結果

[['a', 0, 6, 7, 2, 3, 3, 1, 0, 0, 1], ['b', 1, 1, 11, 6, 0, 2, 1, 4, 1, 2], ['c', 2, 12, 32, 5, 0, 1, 3, 4, 1, 1], ['d', 3, 3, 7, 3, 2, 2, 2, 1, 2, 5], ['e', 4, 6, 6, 3, 5, 1, 1, 1, 1, 3], ['f', 5, 7, 9, 5, 0, 2, 2, 1, 1, 2]]

#columnの計算結果
[[0, 1, 2, 3, 4, 5], [6, 1, 12, 3, 6, 7], [7, 11, 32, 7, 6, 9], [2, 6, 5, 3, 3, 5], [3, 0, 0, 2, 5, 0], [3, 2, 1, 2, 1, 2], [1, 1, 3, 2, 1, 2], [0, 4, 4, 1, 1, 1], [0, 1, 1, 2, 1, 1], [1, 2, 1, 5, 3, 2]]

多次元配列として1行ずつ格納されている事がわかりました．

平均値ベクトルの計算

平均値ベクトルは，以下の数式で表せる事を説明しました．

{ 
  μ = \frac{1}{m} \sum_{i=1}^m x_i
}

これを実際にpythonで記述すると以下のようになります．

# 平均値の計算
for i in range(ROW):
    # スライスという技法
    ave[i] = np.average(row[i][1:len(row[i])])
print(ave)

  Unnamed: 0  1   2   3  4  5  6  7  8  9  10
0          a  0   6   7  2  3  3  1  0  0   1
1          b  1   1  11  6  0  2  1  4  1   2
2          c  2  12  32  5  0  1  3  4  1   1
3          d  3   3   7  3  2  2  2  1  2   5
4          e  4   6   6  3  5  1  1  1  1   3
5          f  5   7   9  5  0  2  2  1  1   2

[2.2999999999999998, 2.8999999999999999, 6.0999999999999996, 3.0, 3.1000000000000001, 3.3999999999999999]

これはrowに対してa行目の値の平均,b行目の値の平均といったように数値が表示されています．

分散共分散行列の計算

分散共分散行列も先日の記事で触れたように，

\sum_{} = \frac{1}{m}\sum_{i=1}^m (x_i - μ)(x_i - μ)^{\mathrm{T}}

このような形で計算する事ができます．

# Numpyのメソッドを使うので，array()でリストを変換した．
column = np.array([column])
ave = np.array(ave)

# 分散共分散行列を求める
# np.swapaxes()で軸を変換することができる．
for i in range(COLUMN):
    diff = (column[0][i] - ave)
    diff = np.array([diff])
    vcm[i] = (diff * np.swapaxes(diff, 0, 1)) / COLUMN

print(vcm)

diffの部分が差分であり，数式的には，

 {(x_i - μ)}

この部分を指しています．
各Columnに対してこの差分を計算し，各列ごとに行列を求めます．

  Unnamed: 0  1   2   3  4  5  6  7  8  9  10
0          a  0   6   7  2  3  3  1  0  0   1
1          b  1   1  11  6  0  2  1  4  1   2
2          c  2  12  32  5  0  1  3  4  1   1
3          d  3   3   7  3  2  2  2  1  2   5
4          e  4   6   6  3  5  1  1  1  1   3
5          f  5   7   9  5  0  2  2  1  1   2

#vcm column1列目の行列
[[[  5.29000000e-01   4.37000000e-01   9.43000000e-01  -0.00000000e+00
    -2.07000000e-01  -3.68000000e-01]
  [  4.37000000e-01   3.61000000e-01   7.79000000e-01  -0.00000000e+00
    -1.71000000e-01  -3.04000000e-01]
  [  9.43000000e-01   7.79000000e-01   1.68100000e+00  -0.00000000e+00
    -3.69000000e-01  -6.56000000e-01]
  [ -0.00000000e+00  -0.00000000e+00  -0.00000000e+00   0.00000000e+00
     0.00000000e+00   0.00000000e+00]
  [ -2.07000000e-01  -1.71000000e-01  -3.69000000e-01   0.00000000e+00
     8.10000000e-02   1.44000000e-01]
  [ -3.68000000e-01  -3.04000000e-01  -6.56000000e-01   0.00000000e+00
     1.44000000e-01   2.56000000e-01]]

#vcm 2列目
 [[  1.36900000e+00  -7.03000000e-01   2.18300000e+00   0.00000000e+00
     1.07300000e+00   1.33200000e+00]
  [ -7.03000000e-01   3.61000000e-01  -1.12100000e+00  -0.00000000e+00
    -5.51000000e-01  -6.84000000e-01]
  [  2.18300000e+00  -1.12100000e+00   3.48100000e+00   0.00000000e+00
     1.71100000e+00   2.12400000e+00]
  [  0.00000000e+00  -0.00000000e+00   0.00000000e+00   0.00000000e+00
     0.00000000e+00   0.00000000e+00]
  [  1.07300000e+00  -5.51000000e-01   1.71100000e+00   0.00000000e+00
     8.41000000e-01   1.04400000e+00]
  [  1.33200000e+00  -6.84000000e-01   2.12400000e+00   0.00000000e+00
     1.04400000e+00   1.29600000e+00]]

…

#vcm 10列目
[[  1.69000000e-01   1.17000000e-01   6.63000000e-01  -2.60000000e-01
     1.30000000e-02   1.82000000e-01]
  [  1.17000000e-01   8.10000000e-02   4.59000000e-01  -1.80000000e-01
     9.00000000e-03   1.26000000e-01]
  [  6.63000000e-01   4.59000000e-01   2.60100000e+00  -1.02000000e+00
     5.10000000e-02   7.14000000e-01]
  [ -2.60000000e-01  -1.80000000e-01  -1.02000000e+00   4.00000000e-01
    -2.00000000e-02  -2.80000000e-01]
  [  1.30000000e-02   9.00000000e-03   5.10000000e-02  -2.00000000e-02
     1.00000000e-03   1.40000000e-02]
  [  1.82000000e-01   1.26000000e-01   7.14000000e-01  -2.80000000e-01
     1.40000000e-02   1.96000000e-01]]]

マハラノビス距離を求める

マハラノビス距離は以下の数式で計算ができます．

  θ < \sqrt{(x_i - μ) ^{\mathrm{T}}\sum{}^{-1} (x_i - μ) }

# mahalnobis distanceを求める
for i in range(COLUMN):
    # 一般逆行列を生成し，計算の都合上転値をかける
    vcm[i] = sc.linalg.pinv(vcm[i])
    vcm[i] = vcm[i].transpose()
    vcm[i] = np.identity(ROW)
    # 差分ベクトルの生成
    diff = (column[0][i] - ave)
    for j in range(ROW):
        tmp[j] = np.dot(diff, vcm[i][j])
    mahal[i] = np.dot(tmp, diff)

#マハラノビス距離
[  5.39258751   8.5720476   28.53559181   3.67151195   7.89176786
   5.88897275   4.72016949   5.00799361   6.7882251    5.8719673 ]

これで，各列のレコードに対して，距離計算をすることが出来ました!

実際にプロットしてみる

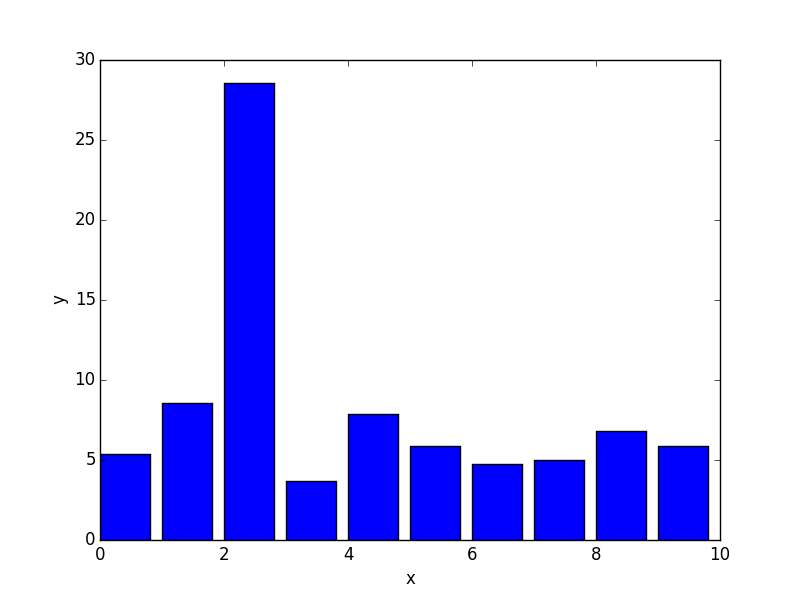
このようにして求めたマハラノビス距離をグラフにプロットしてみます．

plot = pylab.arange(0.0, ROW, 1.0)
mahal = np.sqrt(mahal)

print("マハラノビス距離")
print(mahal)
plt.bar(range(COLUMN),mahal)
plt.title("")
plt.xlabel("x")
plt.ylabel("y")
plt.savefig("plot1.png")

  Unnamed: 0  1   2   3  4  5  6  7  8  9  10
0          a  0   6   7  2  3  3  1  0  0   1
1          b  1   1  11  6  0  2  1  4  1   2
2          c  2  12  32  5  0  1  3  4  1   1
3          d  3   3   7  3  2  2  2  1  2   5
4          e  4   6   6  3  5  1  1  1  1   3
5          f  5   7   9  5  0  2  2  1  1   2

#マハラノビス距離
[  5.39258751   8.5720476   28.53559181   3.67151195   7.89176786
   5.88897275   4.72016949   5.00799361   6.7882251    5.8719673 ]

プロットをしてみると，他の要素に比べて3列目のレコードの距離が大きく離れていることが分かりました．
これで視覚的にデータが異常値となっていることが分かりましたね．

おわりに

いかがでしたでしょうか．
今回は，理論編を踏まえて，実際にpythonを用いてマハラノビス距離を計算してみました．
今回用いたプログラムをGitHubのgistに公開しました．

フルスクラッチで実装したため，コードに不備があるかもしれませんので，精密な計算を要する場合などは，Robust covariance estimation and Mahalanobis distances relevance
この文献を参考にライブラリを用いる事を強くオススメします．

不備や間違い等がありましたらご連絡してくださると幸いです．

111

121

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

	1	2	3	4	5	6	7	8	9	10
a	0	6	7	2	3	3	1	0	0	1
b	1	1	11	6	0	2	1	4	1	2
c	2	12	32	5	0	1	3	4	1	1
d	3	3	7	3	2	2	2	1	2	5
e	4	6	6	3	5	1	1	1	1	3
f	5	7	9	5	0	2	2	1	1	2

	1	2	3	4	5	6	7	8	9	10
a	0	6	7	2	3	3	1	0	0	1
b	1	1	11	6	0	2	1	4	1	2
c	2	12	32	5	0	1	3	4	1	1
d	3	3	7	3	2	2	2	1	2	5
e	4	6	6	3	5	1	1	1	1	3
f	5	7	9	5	0	2	2	1	1	2

	1	2	3	4	5	6	7	8	9	10
a	0	6	7	2	3	3	1	0	0	1
b	1	1	11	6	0	2	1	4	1	2
c	2	12	32	5	0	1	3	4	1	1
d	3	3	7	3	2	2	2	1	2	5
e	4	6	6	3	5	1	1	1	1	3
f	5	7	9	5	0	2	2	1	1	2