はじめに
冬休みの自由研究として、数値流体力学(CFD)の教科書の問題を、C++で書いた自作シミュレータで解いてみました。参照した教科書はこちら:
- 藤井孝藏・立川智章 2020 Pythonで学ぶ流体力学の数値計算方法 オーム社
- 肖鋒・長﨑孝夫 2020 数値流体解析の基礎 -Visual C++とgnuplotによる圧縮性・非圧縮性流体解析- コロナ社
どちらも良書と思いますので、興味のある方はぜひ購入して読み込んでください。ただし、記載されているコードに関しては、わかりやすさを優先しているため、あまり実用的とは言えません。そこで、近年一般的になっている、Pythonでデータの前処理・後処理を行い、C++/C/Fortranで書かれたシミュレータでシミュレーションをするという方法をとることにしましたので、参考にしてください。コードは下記レポジトリで公開しています。
また、1次元オイラー方程式を解くシミュレータも作成しましたので、興味のある方は次の記事もご覧ください。
シミュレータの実装
問題は[2]の第4章にある、速度$c$が一定の一次元移流方程式を周期境界条件のもとで有限差分法を用いて解くという問題を使いました。
$$
\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0
$$
この式の保存型表示
$$
\frac{\partial u}{\partial t} + \frac{\partial f}{\partial x} = 0, \quad f = cu
$$
を離散化しオイラー前進法を適用すると
$$
u_j^{n+1} = u_j^n - \frac{\Delta t}{\Delta x} ( \hat{f}^n _ {j + 1/2} - \hat{f} _ {j - 1/2}^n )
$$
となります。ここで$\hat{f}_{j+1/2}^n$はセル境界$j+1/2$における数値流束です。
数値流束を計算するには、まずセル格子点の値$u_j^n$からセル境界の左側と右側の補間値$u _ {j+1/2}^L$・$u _ {j+1/2}^R$を計算します(空間再構築)。そしてリーマンソルバを使って$u _ {j+1/2}^L$・$u _ {j+1/2}^R$から数値流束$\hat{f} _ {j+1/2}^n$を計算します。
以上をまとめると、アルゴリズムは以下の通りになります。
- 初期化
- $n = 1 \dots N$
- 空間再構築:$u_j^n$から$u_{j+1/2}^L$・$u_{j+1/2}^R$を計算する。
- リーマンソルバ:$u_{j+1/2}^L$・$u_{j+1/2}^R$から$\hat{f}_{j+1/2}$を計算する。
- 時間積分:$u_j^n$・$\hat{f}_{j+1/2}$から$u_j^{n+1}$を求める。
- 境界条件を適用する。
- 計算終了
[2]ではそれぞれのステップに適用する手法を解説しています。
- 空間再構築
- 1次精度
- 2次精度:Beam-Warming, Fromm, Lax-Wendroff法
- TVD法
- リーマンソルバ
- Roeリーマンソルバ
- HLLリーマンソルバ
- Local Lax-Friedrichsリーマンソルバ
- Hartenリーマンソルバ
実装する上で問題となるのは、[2]で紹介されている様々な手法を簡単に切り替えられるようにしなければならないという点ですが、C++ではテンプレートを使えば簡単に実現できます。
template <typename RiemannSolver, typename SpacialReconstructor,
typename TimeIntegrator>
class ScalarAdvectionEquationSimulator {
public:
ScalarAdvectionEquationSimulator(const ProblemParameters& params,
const RiemannSolver& solver,
const SpacialReconstructor& reconstructor,
const TimeIntegrator& integrator)
: n_boundary_cells_{params.n_boundary_cells},
n_domain_cells_{params.n_domain_cells},
n_timesteps_{params.n_timesteps},
solver_{solver},
reconstructor_{reconstructor},
integrator_{integrator},
boundary_{params} {}
/// @brief シミュレーションを実行する
///
/// @param[in] 初期条件
/// @return Eigen::VectorXd シミュレーション終了時の値
template <typename Derived>
Eigen::VectorXd run(const Eigen::MatrixBase<Derived>& u0) const noexcept {
using Eigen::seqN;
using Eigen::VectorXd;
// 両端に境界セルを加える
VectorXd u(this->n_total_cells());
// 領域セルに初期値をコピーする
u(seqN(n_boundary_cells_, n_domain_cells_)) = u0;
// 境界条件を適用する
boundary_.apply(u);
for (int i = 1; i <= n_timesteps_; ++i) {
const VectorXd ul = reconstructor_.calc_left(u); // セル境界左側の値を計算
const VectorXd ur = reconstructor_.calc_right(u); // セル境界右側の値を計算
const VectorXd f = solver_.calc_flux(ul, ur); // 数値流束を計算
integrator_.update(u, f); // 時間積分
boundary_.apply(u); // 境界条件を適用
}
// 両端にある境界セルを除いて、領域セルの値のみを返す
return u(seqN(n_boundary_cells_, n_domain_cells_));
}
private:
int n_total_cells() const noexcept {
return n_boundary_cells_ * 2 + n_domain_cells_;
}
int n_boundary_cells_; ///> 境界セル数
int n_domain_cells_; ///> 領域セル数
int n_timesteps_; ///> タイムステップ数
RiemannSolver solver_; ///> リーマンソルバー
SpacialReconstructor reconstructor_; ///> 空間再構築法
TimeIntegrator integrator_; ///> 時間積分法
PeriodicBoundary boundary_; ///> 周期境界条件
};
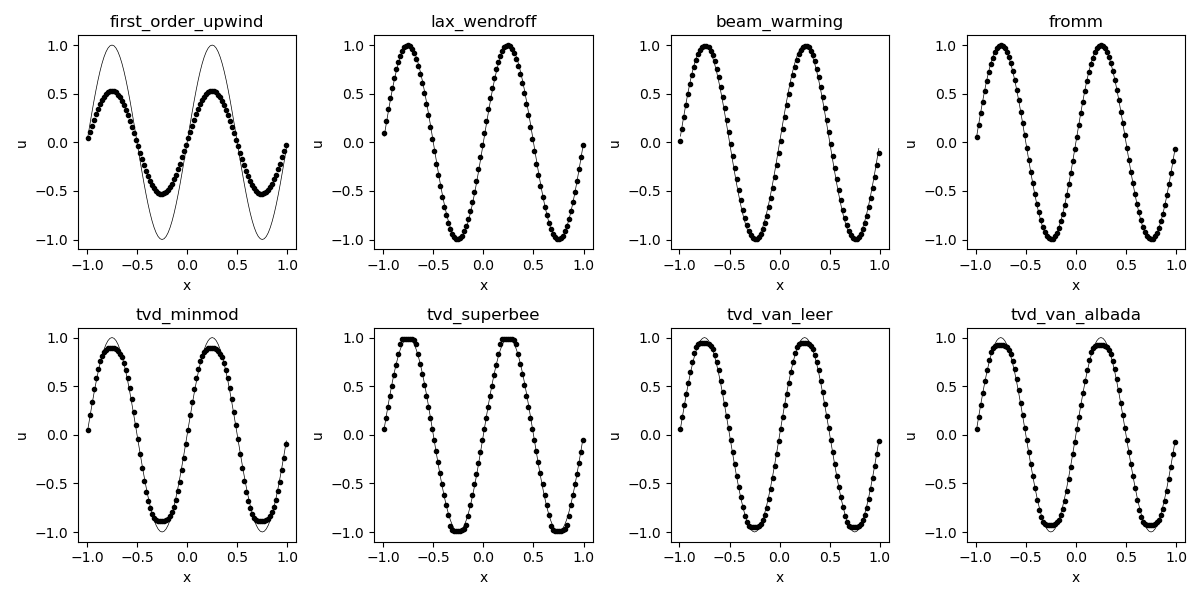
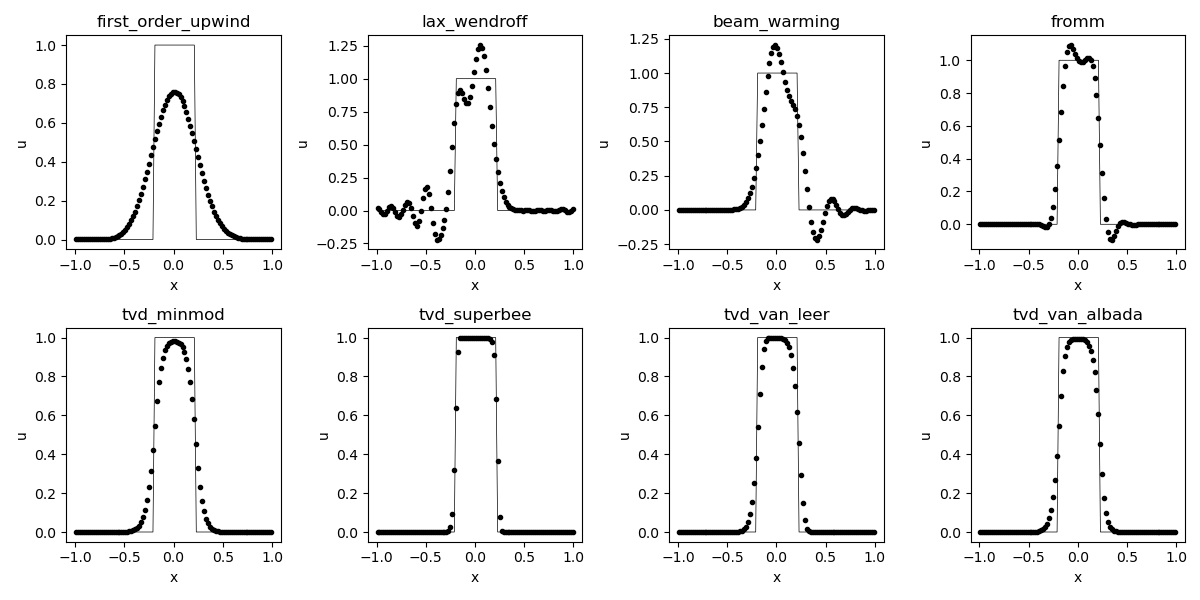
このシミュレータを使って、各手法ごとにメイン関数を作成します。初期条件をサイン波とパルス波としたときの結果をそれぞれファイルに出力するようにしました。
int main(int argc, char** argv) {
using Eigen::VectorXd;
namespace fs = std::filesystem;
const auto params = cfd::make_params();
const VectorXd x = cfd::make_x(params);
const auto simulator =
cfd::make_simulator(params, cfd::RoeRiemannSolver{params.velocity},
cfd::LaxWendroffSpacialReconstructor{params},
cfd::ExplicitEulerScheme{params});
// サイン波
{
const VectorXd u0 = cfd::make_sine_wave(x);
const VectorXd uN = simulator.run(u0);
const auto writer =
cfd::TextFileWriter{fs::path("result/lax_wendroff/sine")};
writer.write(x, "x.txt");
writer.write(u0, "u0.txt");
writer.write(uN, "u500.txt");
}
// パルス波
{
const VectorXd u0 = cfd::make_pulse_wave(x);
const VectorXd uN = simulator.run(u0);
const auto writer =
cfd::TextFileWriter{fs::path("result/lax_wendroff/pulse")};
writer.write(x, "x.txt");
writer.write(u0, "u0.txt");
writer.write(uN, "u500.txt");
}
}
シミュレーション結果の図示
Jupyter Notebookを使って結果を図示しました。
[2]に載っているグラフと同じ結果が得られていますね。
環境について
このシミュレータを作成した環境は以下の通りです。
- OS: Windows 11 Pro
- コンパイラ: MSVC 2022
- ビルドシステム: CMake (Visual Studio付属)
- エディタ: Visual Studio Code
- Python環境: miniconda
Windows上で作成していますが、CMakeとPythonを使っているので、Linux/Mac上でもコンパイルして動かせるはずです。問題が起きたら連絡してください。