はじめに
推薦システムにおいて、ユーザーの好み(preference)を推定する手法は多数提案されていますが、用意する学習データによって適用できる手法はある程度決まります。
ここでは「履歴情報」と「属性情報」の2軸で領域を分類し、推薦システムについてデータの観点から各領域の特性や適用できる手法について自分なりに調べたものを複数回にわたって紹介していきます。
領域の分類
本記事では、履歴情報と属性情報を以下の表のように定義し、次の5つの領域に大別します。
- 時系列情報なし・属性情報なし
- 時系列情報なし・属性情報あり
- シーケンス情報あり・属性情報なし
- シーケンス情報あり・属性情報あり
- セッション情報あり
| 時系列情報なし | ユーザーID・アイテムID・フィードバック(クリックや購入、5段階評価といった行動)の3つの情報で構成される。 | |
| 時系列情報あり | シーケンス情報 |
ユーザー毎に時系列でソートされたフィードバック履歴のリスト情報を持つ。 一人のユーザーに対して1つのリストが存在する。 (例:動画の視聴履歴、など) |
| セッション情報 |
時系列内で明確な範囲(セッション)を持った履歴のリスト情報を持つ。 一人のユーザーに対して1つ以上のリストが存在する。 (例:ネット通販で検索〜購入までを1セッションとする、など) |
|
| 属性情報なし | サービスが属性情報を持っていない | |
| 属性情報あり | ユーザー情報 | 利用者に関する情報(e.g. 年齢、性別、職業、など) |
| アイテム情報 | 推薦される商品に関する情報(e.g. ジャンル、商品写真、商品説明文、など) | |
| インタラクション情報 | ユーザーとアイテムがインタラクションすることで発生する情報(e.g. ページ表示時間、アクセス回数、など) | |
今回の対象
今回は、「時系列情報なし・属性情報なし」と「時系列情報なし・属性情報あり」の2つの領域を見ていきます。
時系列情報なし・属性情報なし
まず、「時系列情報なし・属性情報なし」の領域において用いられるデータとこの領域の特徴、この領域で用いられる手法について紹介します。
入力データ
以下の表のように、「どのユーザー」が「どのアイテム」に対して「どんな評価(フィードバック)」をしたかという情報のみが与えられたデータを用います。
| ユーザーID | アイテムID | フィードバック(5段階評価) |
|---|---|---|
| ユーザーA | アイテムa | 2 |
| ユーザーA | アイテムb | 4 |
| ユーザーB | アイテムb | 3 |
| ユーザーC | アイテムc | 1 |
(余談)explicit feedbackとimplicit feedbackについて
上記のテーブルはexplicit feedbackと呼ばれるフィードバックデータの例になっています。
対になるものとして、implicit feedbackと呼ばれるフィードバックも存在し、その違いは以下になります。
| explicit feedback |
・ユーザーがアイテムに対して明示的に評価した情報(e.g. 5段階評価、like/dislike、など) ・ユーザーのポジティブ・ネガティブ両方の情報を得られ、推薦精度を高めやすい ・一般にデータ収集に対するユーザーの負荷が高く、大量のデータを用意しづらい |
implicit feedback |
・ユーザーがサービスを利用する上で行っている行動に関する情報(e.g. クリック、購入、など) ・ユーザーの選好に関する情報が明示的に得られないため、推薦精度を高めづらい(クリックしなかった ≠ 興味がない) ・容易にデータを収集でき、大量のデータを用意しやすい |
※推薦システムに関する論文では、どちらのフィードバックを対象にしているか明示されていることが多いですが、基本的には損失関数を変えることでモデル構造等を変えることなくどちらのフィードバックにも対応できると思っています。
そのため、本記事では特に明示しない限りexplicit feedbackとimplicit feedbackを区別しません。
explicit feedback向け損失関数の例
- 二乗誤差:$L(u, v) = (r_{uv}-\tilde{r}_{uv})^2$
- $u$: ユーザー
- $v$: アイテム
- $r_{uv}$:ユーザー$u$のアイテム$v$へのフィードバック
- $\tilde{r}_{uv}$:$r_{uv}$の推定値
implicit feedback向け損失関数の例
- BPR Loss:$L(u, v) = -\log(\sigma(\tilde{r}_{uv}-\tilde{r}_{uv_{neg}}))$
- $v_{neg}$:ユーザー$u$の履歴に存在しないアイテム群からネガティブサンプリングしたアイテム
- $\sigma$:シグモイド関数
- 過去に履歴のないアイテムは履歴に存在するアイテムより興味が薄いという仮定のもと、ネガティブデータよりポジティブデータの推定値を大きく学習するよう設計された損失関数
閑話休題
目的
推薦システムの目的は、未知のフィードバック(以下の表の?部分)を推定し、推定値の高い(=好んでもらいやすいと予測した)アイテムを推薦することです。
以下の表のようにユーザーとアイテムを行と列に配置し、各要素の値をフィードバック値で表現したものを「評価値行列」と言います。
| アイテムa | アイテムb | アイテムc | |
| ユーザーA | 2 | 4 | ? |
| ユーザーB | ? | 3 | ? |
| ユーザーC | ? | ? | 1 |
本領域の特徴
- ユーザーの好みが時間とともに変化しないことを暗に仮定している(古いログ・新しいログを区別せず(できず)、同じように扱うため)
- シンプルな問題設定であり、実装が容易で学習や推論に必要な計算資源・時間が少ない場合が多い
- 推薦精度の面では他領域に劣ることがほとんど
アプローチ
ここでは、自分が調べた中で研究事例の多かった行列分解をベースにした手法とグラフをベースにした手法をいくつか紹介します。
行列分解ベース
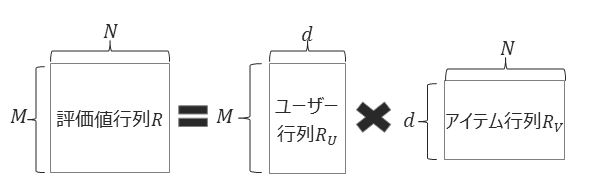
- 評価値行列を$d$次元の潜在ベクトル($d << M, N$, $M$はユーザー数、$N$はアイテム数)を持つ$M$行$d$列のユーザー行列と$d$行$N$列のアイテム行列に分解し、履歴情報をもとにユーザー・アイテム行列のパラメータを学習する方法です
- 損失関数(explicit feedbackの場合)
- $L=\sum_{(u,v)\in S}{(r_{uv}-f(p_u, q_v))^2+\lambda(||p_u||^2+||q_v||^2)}$
- $u$:ユーザー
- $v$:アイテム
- $r_{uv}$:ユーザー$u$のアイテム$v$へのフィードバック
- $S$:履歴集合
- $p_u$:ユーザー$u$の潜在ベクトル
- $q_v$:アイテム$v$の潜在ベクトル
- 推定誤差+正則化項で構成
- $L=\sum_{(u,v)\in S}{(r_{uv}-f(p_u, q_v))^2+\lambda(||p_u||^2+||q_v||^2)}$
- 最適化(学習)手法
- 確率的勾配降下法:データが多いときに有効
- 交互最小二乗法:データが少ないときに有効
- 関数$f$によって複数の手法が存在
- 内積:Matrix Factorization (2009)[1]
- ニューラルネットワーク:Neural Collaborative Filtering (2017)[2]
グラフベース
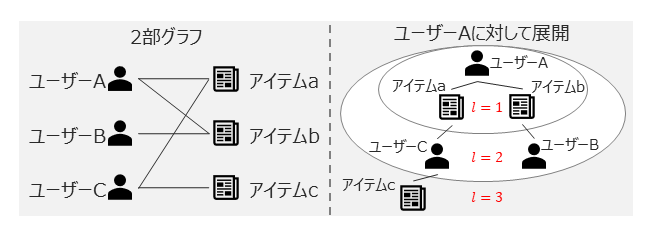
- 履歴情報を2部グラフで表現し、グラフ上でユーザーとアイテムの関係性を伝搬・集約してモデリングする方法です
- 2部グラフをたどっていくことで、ユーザー・アイテム間の関係性だけでなく、ユーザー・ユーザーやアイテム・アイテム間の関係性も考慮することができます
- 伝搬
- ユーザーベクトル:$m_{u\leftarrow v}^{(l)}=f(p_u^{(l-1)},q_v^{(l-1)},\beta_{uv})$
- アイテムベクトル:$m_{v\leftarrow u}^{(l)}=f(q_v^{(l-1)},p_u^{(l-1)},\beta_{uv})$
- 集約
- ユーザーベクトル:$p_u^{(l)}=g(m_{u\leftarrow u}^{(l)}+\sum_{v\in N_u}m_{u\leftarrow v}^{(l)})$
- アイテムベクトル:$q_v^{(l)}=g(m_{v\leftarrow v}^{(l)}+\sum_{u\in N_v}m_{v\leftarrow u}^{(l)})$
- 予測
- $\tilde{r}_{uv}=h([p_u^{(1)};...;p_u^{(L)}])^T\cdot h([q_v^{(1)};...;q_v^{(L)}])$
- 伝搬
- 関数$f,g,h$、パラメータ$\beta_{uv}$のバリエーションによってNGCF (2019)[3]やLightGCN (2020)[4]といった手法が提案されています
所感
- 計算資源の制約や運用負荷の観点から、実用上は一定の需要が残りそう
- 古くから研究が進められている領域であり、性能面での今後の発展性は乏しそう
時系列情報なし・属性情報あり
入力データ
「時系列情報なし」のテーブルに対して、対応するユーザー・アイテムの属性情報が付与されたテーブルを利用します。
| ユーザーID | アイテムID | 年齢 | 性別 | 商品カテゴリ | ・・・ | フィードバック |
|---|---|---|---|---|---|---|
| ユーザーA | アイテムa | 25 | 女 | カテゴリ1 | ・・・ | 2 |
| ユーザーA | アイテムb | 25 | 女 | カテゴリ1 | ・・・ | 4 |
| ユーザーB | アイテムb | 42 | 男 | カテゴリ1 | ・・・ | 3 |
| ユーザーC | アイテムc | 15 | 女 | カテゴリ2 | ・・・ | 1 |
本領域の特徴
- ユーザーの好みが時間とともに変化しないことを暗に仮定している
- 属性情報によるセグメンテーションが可能となり、新規ユーザー・新規アイテムへの推薦精度を高めやすくなる(コールドスタート問題の緩和)
- 属性情報の選定やエンコード方法(文章・画像 → ベクトル化、など)の準備が必要
アプローチ
この領域では、行列分解をベースにした手法とアテンション機構を用いた手法に関する研究が多かったので、その2つについて紹介します。
行列分解ベース
- 2009年にMatrix Factorizationが提案されて以降、その一般化・拡張という形で特徴量間の2次の交互作用を考慮したモデルが2010年頃から発展してきています
- 2次の交互作用の例:年齢 × 性別・・・「10代」の「男性」は「アクション映画」を好む傾向、など。複数の特徴量を組み合わせることで有益な情報が得られる場合がある。
- Factorization Machines (2010)[5]
- Matrix Factorizationモデルを一般化し、全特徴量間の2次の交互作用まで考慮した手法
- $\tilde{r}=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{(i,j)}(z_i\cdot z_j)x_ix_j$
- $w_0$は全体のバイアス項、$w_i$は特徴量$i$の1次作用項
- $z_i$は特徴量$i$に対応する$d$次元潜在ベクトル
- Field-aware Factorization Machines (2016)[6]
- 課題:Factorization Machinesにおいて特徴量と潜在ベクトルが1対1対応の場合、他特徴量との交互作用を単一ベクトルで表現する必要があり、表現力が不足している
- アプローチ:Factorization Machinesにフィールドという概念を導入し、フィールドの数だけ特徴量ごとに潜在ベクトルを用意してモデルの表現力を向上
- $\tilde{r}=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{(i,j)}(z_{i,F_j}\cdot z_{j,F_i})x_ix_j$
- $z_{i,F_j}$は特徴量$x_i$が特徴量$x_j$との交互作用を考慮する際に用いる潜在ベクトル
- フィールドという概念を導入して上記のようなモデルに拡張することで、特徴量の種類によって適用する潜在ベクトルを切り替えることができるようになる
アテンションベース
- モデルのどこかにアテンション機構を導入し、特徴量の重要度や交互作用項を学習する手法が提案されています
- Attentional Factorization Machines (2017)[7]
- 課題:Factorization Machinesは強力な手法だが、すべての交互作用項を同一に扱ってしまい、予測に不要な交互作用項がノイズとなって性能低下を引き起こす恐れがある
- アプローチ:Factorization Machinesの交互作用項の重要度をアテンション機構で学習
- $\tilde{r}=w_0+\sum_{i=1}^{n}w_ix_i+\sum_{(i,j)}\alpha_{i,j}(z_i\cdot z_j)x_ix_j$
- $\alpha_{i,j}$は特徴量$i$と$j$の交互作用項の重要度を表します
- $\alpha_{i,j}^{'}=h^T\cdot$ ReLU$(W(z_i\cdot z_j)x_ix_j+b)$
- $\alpha_{i,j}=\frac{\exp(\alpha_{i,j}^{'})}{\sum_{k,l}\exp(\alpha_{k,l}^{'})}$
- $W,b,h$は学習用パラメータ
- 従来のFactorization Machinesベースの手法では2次の交互作用項の重要度$\alpha_{i,j}$が一律だったため、ここを可変にしてデータから学習しようという発想の手法になっています
- AutoInt (2019)[8]
- 対象:Click-through rate(CTR)の予測(CTRはWeb上の広告配信などで重要な指標)
- 課題
- 入力情報がスパースで高次元 → 有益な情報を抽出することが難しい
- 高次の交互作用によって高精度の予測が可能と考えられるが、そういった特徴量エンジニアリングは高コスト & ドメイン毎にエンジニアリングが必要
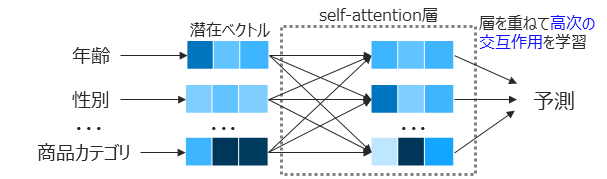
- アプローチ:特徴量間の交互作用をself-attentionによって学習
- 特徴量を潜在空間に写像
- カテゴリカル特徴量:$e_i=\frac{1}{q}V_ix_i$($q$は該当する要素の数。商品のジャンルなどは複数に該当する場合があり、$q>1$となる)
- 連続値特徴量:$e_m=v_mx_m$($x_m$は連続値特徴量$m$のスカラー値、$v_m$は特徴量$m$のエンべディングベクトル)
- Multi-head self-attention機構を用いて、どの特徴量間の交互作用がどのような軸で重要になるかを学習
- フィードバックの予測
- $\tilde{r}=f([e^{(1)};...;e^{(L)}])$
- $e^{(l)}$は$l$層目の出力(※論文ではスキップコネクションも入るが、簡易的な説明のため省略)
- $\tilde{r}=f([e^{(1)};...;e^{(L)}])$
- 特徴量を潜在空間に写像
- モデル内で自動的に特徴量間の高次の交互作用を学習できるため、特徴量エンジニアリングが不要となり様々なドメインへ適用しやすい手法となっています
所感
- 属性情報の活用に関する研究は依然として発展の余地がありそう(ドメイン特有の特徴量を活用・強調したモデル[9]の提案が最近でも存在)
- 特徴量の重要度に関するアテンションマップはマーケティング分析業務等へ活用できそうなので、そういった解釈性に関する研究についても調査していきたいです
簡易検証
最後に、ここまでで紹介した手法をいくつかのデータセットに対して適用し、性能がどれくらい違うのか確認してみたいと思います。
データセット
- explicit feedbackデータセット
- Movielens-1m:視聴した映画に対して5段階で評価したデータセット
- ModCloth:購入した衣服に対して5段階で評価したデータセット
- implicit feedbackデータセット
- Last.FM:音楽の再生履歴
- DIGINETICA:e-commerceの検索エンジンにおけるクリック・購入の履歴
※explicit feedbackデータについては、5段階評価で4以上を1、4未満を0とした2値分類に変換して利用します(2値分類しか対応しないモデルが存在するため)
| データセット | ドメイン | ユーザー数 | アイテム数 | データ数 | sparsity[%] | 採用理由 |
|---|---|---|---|---|---|---|
| Movielens-1m | 映画 | 6,040 | 3,706 | 1,000,209 | 95.5 | 最もポピュラーなデータセットのため |
| ModCloth | ファッション | 47,958 | 1,378 | 82,790 | 99.9 | アイテム数が少ない設定での性能が見たいため |
| Last.FM | 音楽 | 1,892 | 17,632 | 92,834 | 99.7 | 比較的ポピュラーなデータセットのため |
| DIGINETICA | e-commerce | 204,789 | 43,136 | 993,483 | 99.9 | 自分の興味のあるドメインのため |
※sparsity = (1 - データ数 / (ユーザー数 × アイテム数)) × 100。値が大きいほどデータセットのスパース性が高く、ユーザーの好みが推定しづらい。
モデル
- explicit feedback向け
- Matrix Factorization[1]
- Factorization Machines[5]
- Field-aware Factorization Machines[6]
- Attentional Factorization Machines[7]
- AutoInt[8]
- implicit feedback向け
- Neural Collaborative Filtering[2]
- NGCF[3]
- LightGCN[4]
※1 今回、RecBoleというライブラリの実装を利用するのですが、実装が論文準拠となっており、損失関数を変えて各フィードバック用に学習するといったことが簡単にはできなさそうだったので、モデルごとに適用するデータセットを変えています。
※2 ハイパーパラメータはRecBole実装のデフォルト値を使います。ただし、Field-aware Factorization Machinesのフィールドはユーザー属性情報とアイテム属性情報の2つのフィールドで分けています。
Matrix FactorizationのみRecBoleに実装がなかったので、自分で実装しました(ハイパーパラメータは下記コード内のデフォルト値を使っています)。
import torch
import torch.nn as nn
from recbole.model.abstract_recommender import GeneralRecommender
from recbole.model.init import xavier_normal_initialization
from recbole.utils import InputType
class MF(GeneralRecommender):
input_type = InputType.POINTWISE
def __init__(self, config, dataset):
super(MF, self).__init__(config, dataset)
# load dataset info
self.RATING = config["LABEL_FIELD"]
# load parameters info
if "embedding_size" in config:
self.embedding_size = config["embedding_size"]
else:
self.embedding_size = 100
if "biased" in config:
self.biased = config["biased"]
else:
self.biased = True
if "reg_weight_2" in config:
self.reg_weight_2 = config["reg_weight_2"]
else:
self.reg_weight_2 = 0.01
# define layers and loss
self.user_embedding = nn.Embedding(self.n_users, self.embedding_size)
self.item_embedding = nn.Embedding(self.n_items, self.embedding_size)
self.user_bias = nn.Parameter(torch.zeros(self.n_users))
self.item_bias = nn.Parameter(torch.zeros(self.n_items))
self.loss = nn.MSELoss(reduction="sum")
# parameters initialization
self.apply(xavier_normal_initialization)
def forward(self, user, item):
user_e = self.user_embedding(user)
item_e = self.item_embedding(item)
output = torch.mul(user_e, item_e).sum(dim=1)
if self.biased:
output += self.user_bias[user] + self.item_bias[item]
return output
def calculate_loss(self, interaction):
user = interaction[self.USER_ID]
item = interaction[self.ITEM_ID]
rating = interaction[self.RATING]
output = self.forward(user, item)
loss = self.loss(output, rating)
# L2-regularization
if self.biased:
user_e = torch.cat([self.user_embedding(user).detach(), self.user_bias[user].unsqueeze(-1).detach()], dim=1)
item_e = torch.cat([self.item_embedding(item).detach(), self.item_bias[item].unsqueeze(-1).detach()], dim=1)
else:
user_e = self.user_embedding(user).detach()
item_e = self.item_embedding(item).detach()
loss += self.reg_weight_2 * (user_e.norm(p=2, dim=1).sum() + item_e.norm(p=2, dim=1).sum())
return loss
def predict(self, interaction):
user = interaction[self.USER_ID]
item = interaction[self.ITEM_ID]
return self.forward(user, item)
def full_sort_predict(self, interaction):
user = interaction[self.USER_ID]
user_e = self.user_embedding(user)
all_item_e = self.item_embedding.weight
score = torch.matmul(user_e, all_item_e.transpose(0, 1))
if self.biased:
score += self.user_bias[user].unsqueeze(-1) + self.item_bias.unsqueeze(0)
return score.detach().view(-1)
結果・考察
explicit feedbackデータセットの結果
| モデル | データセット | モデルパラメータ数 | MAE | RMSE | 実行時間[s] |
|---|---|---|---|---|---|
| MF | ml-1m | 497,148 | 0.45 | 0.52 | 192 |
| FM | ml-1m | 502,861 | 0.35 | 0.42 | 197 |
| FFM | ml-1m | 1,488,861 | 0.34 | 0.42 | 263 |
| AFM | ml-1m | 505,461 | 0.33 | 0.42 | 508 |
| AutoInt | ml-1m | 591,481 | 0.34 | 0.42 | 394 |
| MF | ModCloth | 2,516,238 | 0.55 | 0.59 | 21.3 |
| FM | ModCloth | 2,523,991 | 0.37 | 0.44 | 12.5 |
| FFM | ModCloth | 9,947,491 | 0.38 | 0.44 | 20.7 |
| AFM | ModCloth | 2,526,591 | 0.37 | 0.44 | 25.8 |
| AutoInt | ModCloth | 2,631,961 | 0.40 | 0.45 | 16.8 |
※MF:Matrix Factorization, FM:Factorization Machines, FFM:Field-aware Factorization Machines, AFM:Attentional Factorization Machines
- 属性情報を使わないMFは他手法と比べて明らかに性能が低い(自分の実装が悪い可能性あり)
- データのスパース性が高い場合(ModCloth)、シンプルな手法(FM, AFM)が高い性能
- データ量が多い場合(ml-1m)、比較的複雑なモデル(FFM, AutoInt)でも高い性能を達成
- 複雑なモデルはデータが少ないと過学習して性能が出づらいと考えられる。また、データ量が100万程度であればモデル間で性能は大差なく、実行時間的にもFMなどシンプルな手法で十分な場合が多そう。
implicit feedbackデータセットの結果
| モデル | データセット | モデルパラメータ数 | MRR@10 | nDCG@10 | 実行時間[s] |
|---|---|---|---|---|---|
| NeuMF | Last.FM | 2,524,225 | 0.26 | 0.15 | 247.2 |
| NGCF | Last.FM | 1,274,624 | 0.33 | 0.18 | 490.6 |
| LightGCN | Last.FM | 1,249,664 | 0.30 | 0.17 | 365.4 |
| NeuMF | DIGINETICA | 31,759,553 | 0.86 | 0.89 | 3,044 |
| NGCF | DIGINETICA | 15,892,288 | 0.94 | 0.95 | 12,448 |
| LightGCN | DIGINETICA | 15,867,328 | 0.94 | 0.95 | 9,058 |
※1 NeuMF:Neural Collaborative Filtering
※2 DIGINETICAデータセットはデータ量が多く、全データを評価するのは困難だったため、ポジティブなアイテム1件に対してネガティブサンプリングで10件取り、計11個のアイテム内でのtop-10性能を示しています。そのため、DIGINETICAデータセットにおける性能は非常に高くでています。あくまで手法間の相対的な比較として見てください。
- いずれのデータセットでも、行列分解ベース手法(NeuMF)よりグラフベース手法(NGCF, LightGCN)の方が推薦精度は優れる
- ユーザー・アイテム間だけでなく、ユーザー・ユーザー、アイテム・アイテム間の交互作用も間接的に考慮できることの寄与が大きいと考えられる
- NGCFとLightGCNは推薦精度に大きな差が無いため、シンプルで実行時間の短いLightGCNを選べば良さそう
- ハイパーパラメータはチューニングしていない点に注意が必要(調整するパラメータが結構あるので、性能に対してセンシティブなパラメータが存在する可能性あり)
まとめ
今回は「時系列情報なし・属性情報なし」と「時系列情報なし・属性情報あり」の領域に焦点を当て、領域の特性や提案されている技術・手法を紹介しました。
紹介した手法は「行列分解」・「グラフニューラルネットワーク」・「アテンション機構」といった技術がキーワードとなっており、これらの技術をどれだけうまく設計できているかが手法間での違いとなっていました。
また、簡易的な検証も行い、以下のことを確認しました。
- explicit feedbackデータでは昔の手法でも十分に通用し、データセットの規模によってはシンプルな昔の手法の方が優れる場合もある
- implicit feedbackデータではグラフベースの手法が優れており、ユーザー・ユーザーやアイテム・アイテム間の交互作用を考慮することが重要そうである
- データセットの規模感によって強みを発揮する手法が異なるため、そのあたりは検討が必要そうである
参考
- Yehuda Koren, et al., "Matrix Factorization Techniques for Recommender Systems" Computer (2009)
- Xiangnan He, et al., "Neural Collaborative Filtering" WWW'2017
- Xiang Wang, et al., "Neural Graph Collaborative Filtering" SIGIR (2019)
- Xiangnan He, et al., "LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation" SIGIR (2020)
- Steffen Rendle, "Factorization Machines" IEEE International Conference on Data Mining (2010)
- Yuchin Juan, et al., "Field-aware Factorization Machines for CTR Prediction" RecSys (2016)
- Jun Xiao, et al., "Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks", IJCAI (2017)
- Weiping Song, et al., "AutoInt: Automatic Feature Interaction Learning via Self-Attentive Neural Networks" CIKM (2019)
- Wanjie Tao, et al., "SMINet: State-Aware Multi-Aspect Interests Representation Network for Cold-Start Users Recommendation" AAAI (2022)