はじめに
この記事は、統計初心者学生が、ベイズ統計での心理統計学の授業に必死についていくために作成したゆるいメモ程度の内容のため、間違い等々があるかもしれません。ご指摘等頂ければ幸いです。
同じ境遇の方、一緒に頑張りましょう。
内容は適宜追加予定です。
TL;DR
ミュラーリヤー錯視実験における錯視量の、事後分布のパラメータの点推定・区間推定をベイズ推定法で行った。
用語の説明
ミュラーリヤー錯視とは
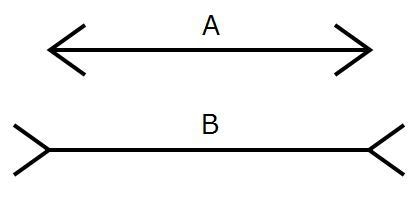
同じ長さの線分でも、外向きの斜線に挟まれた場合(図形B)の方が、内向きの斜線に挟まれた場合(図形A)よりも長く知覚されるといった錯視の一種です。実際の線分の長さと知覚した線分の長さとの差を、錯視量と呼びます。
ベイズ推定法とは
ベイズ推定の説明に移る前に、比較する対象として従来法の代表である最尤推定法を取り上げ、モデルとデータの関係のとらえ方の違いについて述べます。
最尤推定法
最尤推定法におけるモデルとデータの関係は、真値(真のモデル)は一つに決まっており、データは真のモデルから発生した確率的なものであるため、取り方によって確率的に変化するという考え方をします。
コイントスを例に挙げると、真値が確率0.5でも、実際には0.8だったり0.3だったりします。しかし、何度もコイントスを繰り返して平均を取れば、0.5に近づいていくはず…
データを固定して考えた場合に、このデータが最も得られやすいモデルはどのようなものだろう?と考えるのが尤度の考え方であり、尤度が最大になるモデルを推定する方法が最尤推定法となります。
ベイズ推定法
一方、ベイズ推定では、真値を確率分布として考えます。そのため、データはあくまで情報であり、どんどんデータを加えて更新していけば、現象をより説明することのできる分布(=真値の分布)を推定することができるという考え方をします。
このとき、母数がどのあたりにあるかに関する、データを見る前の主観的な信念の確率分布を事前分布と呼び、データを得た後更新された母数の分布を事後分布と呼びます。
ベイズ統計学はベイズの定理を使用して現象のモデル化を行います。事後分布は簡単に言うと次の式で計算されます。
事後分布 = (事前分布×尤度)/ データの分布(正規化定数)
最尤推定法は尤度だけ(正確には一様分布をかけている)から真値を推定しますが、ベイズ推定法では尤度が事前分布の影響を受けており、事後分布は尤度と事前分布の積から推定されます。よって、客観性・公平性を期するために、分析で使う事前分布には事後分布にできるだけ影響しない、無情報的事前分布を選ぶことがミソとなります。
詳しくは、社会心理学を専門とされる大学の教員の方が書かれた記事に従来の最尤推定法との違いや、利点・欠点がわかりやすく書かれていますので、そちらをご参照ください(先ほどの説明は引用記事のほぼパクリです)。
MCMC法
事後分布は、(事前分布×尤度)/データの分布 で導けるのでした。しかし、解析的にデータの分布(正規化定数の積分)を解くのは難しいらしいです。そこで、ベイズ推定では「MCMC法」と呼ばれるアルゴリズムを用い、事後分布に従う母数を乱数として発生させ、事後分布をあたかもデータ分布のように入手します。また、得られた乱数列をチェインと呼びます。
今回やりたいこと
用語の軽い説明が終わったところで、今回やりたいことの確認です。
今回は、ミュラーリヤー錯視実験で観測された後の、事後分布のパラメータ
- 1.$\mu$の点推定(「錯視量」の平均$\mu$は何mmか?)
- 2.$\mu$の区間推定(「錯視量」の平均$\mu$は何mm~何mmの区間にある?)
- 3.$\sigma$の点推定(「錯視量」の平均的な知覚の散らばり$\sigma$は何mm?)
- 4.$\sigma$の区間推定(「錯視量」の平均的な知覚の散らばり$\sigma$は何mm~何mmの区間にある?)
をしたい!ということで、ベイズ推定法を使って分析を行っていきます。
設定
ある参加者に対してミュラーリヤー錯視の実験を10回試行した結果、図形Aに対する錯視量(実際の線分の長さと知覚した長さの差)は,
23,21,19,22,20,17,22,18,20,25
だったそうです。今回はこのデータを利用して、分析を行っていきます。
動作環境
分析
下準備
import numpy as np
import scipy as sp
import scipy.stats as stats
import pandas as pd
from IPython.core.pylabtools import figsize
from matplotlib import pyplot as plt
データの準備
observed_data_list = [23,21,19,22,20,17,22,18,20,25]
observed_data = pd.Series(observed_data_list)
事後分布のサンプリング
PyMC3と呼ばれるPythonライブラリを使って、事後分布のサンプリングを行います。
今回は事後分布に正規分布モデルを仮定しています。よって、推測するパラメータは$\mu$と$\sigma$の2つです。
ここで、ベイズ推定法の考え方はパラメータも何らかの確率分布であり、固定値ではない・・・というものでした。
そのため、パラメータである$\mu$と$\sigma$も、何らかの事前分布を仮定する必要があります。
今回の母平均$\mu$と母標準偏差$\sigma$の事前分布には一様分布を仮定しており、そのパラメータは主観的にならないように十分に広い範囲に設定します。
また、今回発生させる乱数を25000個とし、チェインを5つ発生させています。
import pymc3 as pm
with pm.Model() as model:
# 事前分布
mu = pm.Uniform('mu', 10, 35)
sigma = pm.Uniform('sigma', 1, 9)
# 尤度
ml = pm.Normal('ml', mu=mu, sd=sigma, observed=observed_data)
# サンプリング
trace_g = pm.sample(25000)
バーンイン(焼き捨て)
生成した最初から5000個の乱数は、事後分布に従う乱数でない可能性が高い為、捨て(バーンイン)ます。
chain_g = trace_g[5000:]
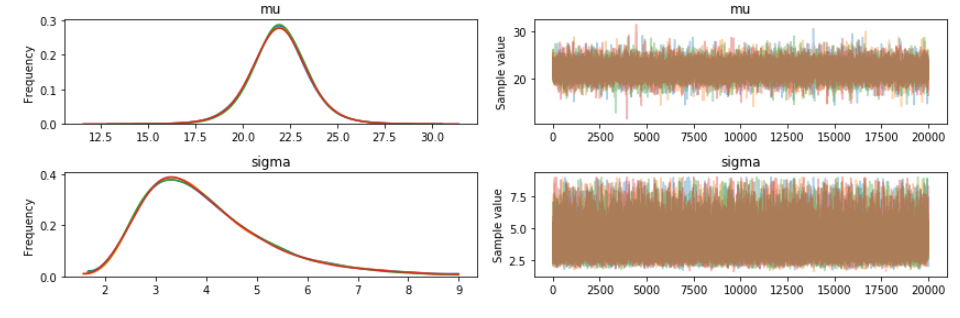
推測した事後分布の図示
pm.traceplot(chain_g)
plt.figure()
事後分布の要約統計量の算出
pm.summary()
pm.summary()とすると、事後分布の要約統計量が算出できます。
$\hat{R}$はMCMCのモデルにあった乱数を発生させているかどうかを判断する指標で、1に近いほど良いらしいです。
分析結果
1.事後分布の平均値の点推定
事後分布の平均値は(=事後期待値(expected a posteriori,EAP))と呼ばれます。
表から、$\mu$に関するEAPは、$\hat{\mu_{eap}}=$21.39mmでした。
2.事後分布の平均値の区間推定
表の2.5%点と97.5%点を参照し、**$\mu$の両側確信区間は[18.83mm, 24.85mm]**でした。
3.事後分布の標準偏差の点推定
表から、$\sigma$に関するEAPは、$\hat{\sigma_{eap}}$=4.00mmでした。
4.事後分布の標準偏差の区間推定
表の2.5%点と97.5%点を参照し、**$\sigma$の両側確信区間は[2.00mm, 6.61mm]**でした。
終わりに
仮説検定からの脱却、ということでベイズ統計の勉強を始めましたが、書籍等を読んでいるとチェインとかバーンインとかの単語が飛び交い、またパラメータを得るまでの手続きがややこしいため、途中で**「結局これは何をしているんだ?」**といった箇所が度々あります。
今まで統計ソフトでバーン!と結果を脳死で算出してきた身からすると、**母集団のパラメータを推定するだけでこんな労力が必要なのか・・・**と脳がパンク寸前です。
【追記】
どうやら、ベイズ統計界隈で色々考え方や解釈の違い等で議論が起こっているようです。そのため、この記事の内容も、一つのメモ程度として見ることをお勧めします。