StanとRでベイズ統計モデリング(アヒル本)をPythonにしてみる - 12.3 変化点検出

実行環境

インポート

import numpy as np
import pandas as pd
import pystan
import matplotlib.pyplot as plt
from matplotlib.figure import figaspect
%matplotlib inline

データ読み込み

changepoint = pd.read_csv('./data/data-changepoint.txt')

12.3 変化点検出

data = dict(
    T=changepoint.index.size,
    Y=changepoint['Y']
)
stanmodel = pystan.StanModel('./stan/model12-7.stan')
fit = stanmodel.sampling(data=data, pars=('mu', 's_mu', 's_Y'), seed=1234, n_jobs=-1)

_, (ax1, ax2) = plt.subplots(1, 2, figsize=figaspect(3/8), sharex=True, sharey=True)

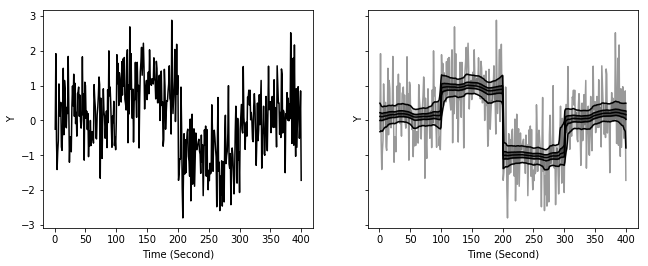
ax1.plot('X', 'Y', data=changepoint, color='k')
plt.setp(ax1, xlabel='Time (Second)', ylabel='Y')

ms = fit.extract()
probs = (2.5, 25, 50, 75, 97.5)
columns = ['p{}'.format(p) for p in probs]
d_est = pd.DataFrame(np.percentile(ms['mu'], probs, axis=0).T, columns=columns)
d_est['x'] = d_est.index + 1
ax2.fill_between('x', 'p2.5', 'p97.5', data=d_est, color='k', alpha=0.2)
ax2.fill_between('x', 'p25', 'p75', data=d_est, color='k', alpha=0.4)
for col in columns:
    ax2.plot('x', col, data=d_est, color='k')
ax2.plot('X', 'Y', data=changepoint, color='k', alpha=0.4)
plt.setp(ax2, xlabel='Time (Second)', ylabel='Y')

plt.show()