StanとRでベイズ統計モデリング(アヒル本)をPythonにしてみる - 10.1 パラメータの識別可能性

実行環境

インポート

import numpy as np
from scipy import stats
import pandas as pd
import statsmodels.api as sm
import pystan
import matplotlib.pyplot as plt
from matplotlib.figure import figaspect
%matplotlib inline

データ読み込み

category = pd.read_csv('./data/data-category.txt')
usagitokame = pd.read_csv('./data/data-usagitokame.txt')

10.1 パラメータの識別可能性

10.1.3 ラベルスイッチング

np.random.seed(123)

N = 200
a = 0.3
d1 = np.random.normal(loc=0, scale=2, size=N)
d2 = np.random.normal(loc=-4, scale=1, size=N)
d3 = np.random.uniform(size=N) <= a
Y = d1*d3 + d2*(1-d3)
X = np.linspace(Y.min(), Y.max(), 100)

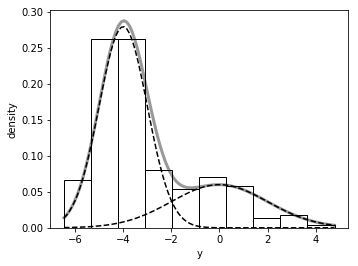
plt.figure(figsize=figaspect(3/4))
ax = plt.axes()
ax.hist(Y, facecolor='w', edgecolor='k', density=True)
ax.plot(X, a*stats.norm.pdf(X, loc=0, scale=2), c='k', linestyle='dashed')
ax.plot(X, (1-a)*stats.norm.pdf(X, loc=-4, scale=1), c='k', linestyle='dashed')
ax.plot(X, a*stats.norm.pdf(X, loc=0, scale=2) + (1-a)*stats.norm.pdf(X, loc=-4, scale=1), c='k', alpha=0.4, linestyle='solid', linewidth=3)
plt.setp(ax, xlabel='y', ylabel='density')
plt.show()

10.1.4 多項ロジスティック回帰

X = sm.add_constant(category.iloc[:, :-1])
X['Age'] /= 100
X['Income'] /= 1000
data = dict(
    N=category.index.size,
    D=X.columns.size,
    K=category['Y'].max(),
    X=X,
    Y=category['Y']
)
fit = pystan.stan('./stan/model10-2.stan', data=data, seed=1234)

10.1.5 ウサギとカメ

np.random.seed(123)

G = 30
mu_pf = (0, 1.5)
pf = np.random.normal(loc=mu_pf, scale=1, size=(G, 2))
d = pd.DataFrame(np.argsort(pf, axis=1)+1, columns=('Loser', 'Winner'))
tbl = pd.crosstab([], d['Winner'])
tbl

data = dict(
    N=usagitokame.columns.size,
    G=usagitokame.index.size,
    LW=usagitokame
)
fit = pystan.stan('./stan/model10-3.stan', data=data, seed=1234)