この記事について
Grover Searchのアルゴリズムでは、、
Grover Operatorを、データ数Nに対して$\sqrt{N}$回適用することで所望の状態を得てデータ検索が実現できる事がわかっています。この背景で、
- データ数Nに対して、$O(\sqrt{N})$のオペレータ適用でデータ検索ができる!
- 古典の線形サーチ$O(N)$よりも効率的な探索ができる!
といった説明となるのですが、、
Grover Operatorの適用回数が$\sqrt{N}$回よりも、大きくても小さくても、所望の状態を得られない。が実際であり事実であると理解しています。
つまり、いい塩梅が重要となります。
このいい塩梅がデータ数Nに対し$\sqrt{N}$回という点がわかりやすいように、実験的な記事を作ってみました。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
QuirkでGrover Search
起動してみる
本稿では、量子計算のシミュレータとしてQuirkを利用します。
Qurikを起動すると、標準サンプルとしてGrover Searchがあるのでこれを利用します。

Grover Searchを選択すると、回路が表示されます。
Grover Operatorを適正回数適用する
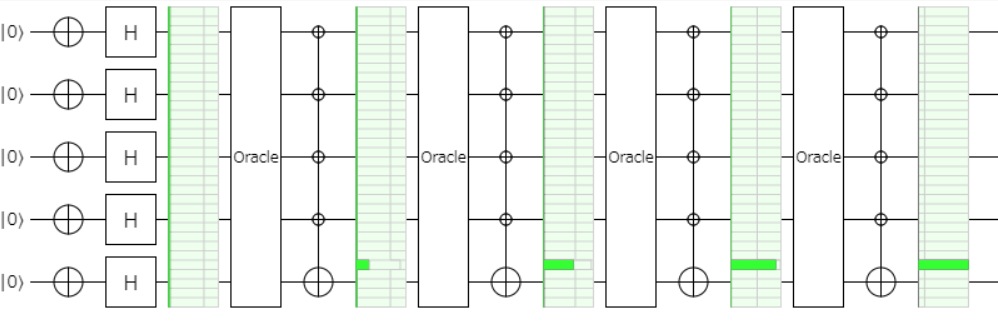
上述のOracleとIAMを適正回数($\sqrt{N}$回)適用したいので、下記のような回路となります。
$\sqrt{N}$回以前で観測したら、どうでしょうか?
検索対象データに対応する確率(確率振幅)は下記の通りでやはり4回目でピークを迎えます。
| 1回目 | 2回目 | 3回目 | 4回目 |
|---|---|---|---|
| 25% | 60% | 89% | 99% |
 |
 |
 |
 |
素朴な疑問
上記結果だけでは、Grover Operatorを適用すれば適用するほどに検索対象データに対応する確率が100%に近い状態で結果を取り出せるように見えます。
では、5回目以降はどのような確率(確率振幅)になるかが気になります。
そこで、実験的に、適正回数以上に過剰にGrover Operatorを適用してみたいと思います。
Grover Operatorを過剰に適用する
適正が4回だったのでその倍の8回、オペレータを適用してみましょう。

1回目~4回目は上記と変わらないので5~8回目について確認します。下記に示しますが、
適正回数以上にオペレータを適用すると検索対象の確率(確率振幅)は、なんと減衰します。。
| 5回目 | 6回目 | 7回目 | 8回目 |
|---|---|---|---|
| 85% | 54% | 21% | 1.4% |
 |
 |
 |
 |
最適なオペレータの適用回数について
Quantum Native dojo 8.2にも解説があるとおり、所望の$\ket{\beta}$に対して、$\ket{s}$が最も近づくタイミングが、計算により求められ、それが$\sqrt{N}$となります。詳細はQuantum Native dojo 8.2を参照いただければと思います。
恐縮ですが、リンクさせていただきます。

まとめ
Grover Searchの特徴ですが、下記は事実です。
- データ数Nに対して、$O(\sqrt{N})$のオペレータ適用でデータ検索ができる!
ただし、$\sqrt{N}$で効率的にデータ探索ができるとう言葉を正しく解釈すると、所望の結果が得られるオペレータ適用回数が$\sqrt{N}$回であって、Grover Searchはいい塩梅が重要というのが本質な気がします。
中を覗き見したくても、測定したら量子状態は破壊されるので、いい塩梅まで我慢して、待って待って良いタイミングで測定する。そんな、Grover Searchのご紹介でした。
(補足)サンプルのGrover Operatorについて
Grover Searchは下記の2つの操作から構成されるGrover Operatorをデータ数Nに対して、$\sqrt{N}$回適用し解を得るアルゴリズムです。
- データをマーキングずるためのOracle
- マーキングしたデータに対応する振幅を増幅するためのIAM(Inversion About Mean)
これらが、Quirkのサンプル上では、下記の様の実装されています。
Oracle
Toolbox2のOracleにマウスオーバすると表示されるのですが、事前定義の回路として下記のようにOracleが定義されています。これにより検索対象に対してマーキングを行います。

Inversion About Mean(IAM)
Oracleでマーキングした検索対象に対応する確率振幅を増幅するためのIAMが必要ですが、一般的には検索対象ビットに対する$H^{\otimes N}$と位相シフトの$Controlled-Z$で構成されます。

一方で、サンプルの量子回路上でのIAM相当の部分は、下記のようになっています。

このゲートについては、https://algassert.com/post/1706 に解説があるのですが、$H$で挟まれる$Controlled-U$相当の操作が行われるゲートの様で、このゲートでIAM相当の振幅増幅ができるようです
