はじめに

皆さんは、機械学習とか回帰分析を行ったことはあるでしょうか？
与えられた「データ」に対して、「回帰モデル」を作成したときに、データに対するモデルの
当てはまりの良さを表現する指標として、決定係数というものがあります。
（決定係数とかr2とか呼ばれたりもします。）

R^2 = 1 - \frac{\displaystyle\sum_{i=1}^{n}( y_i - \hat{y_i})^2}{\displaystyle\sum_{i=1}^{n}(y_i - \overline{y})^2} = 1-\frac{残差変動}{全変動}

数式が苦手な人からすると、この式を見ただけで「うぎゃ」ってなりそうなので、、
この式のこころを、中学数学で理解してみよう。という内容です。
使うのは、中学数学で勉強する１次関数だけです。

y = ax + b
\ \ \ \ \ \ \ \ 
a:傾き,b:切片

傾きと切片くらいは利用させていただくとして、初学者向けに記事を書いてみますので、
厳密性や正確性は犠牲にしても、なるべく優しく書いて見ようと思います。
まずは、この記事でイメージ程度（数式のこころ）を掴んで頂ければと。

説明の進め方

1.「データにモデルを当てはめる」回帰分析を説明します
2. 次に、切片しか調整できない「意地悪なモデル」を考えます
3. そして、傾きも切片も調整できる「通常のモデル」を考えます
4. 最後に、決定係数R2の意味を解釈していきたいと思います

回帰分析って

対象データ

例えば、下記のようなデータを手に入れたとします。
データにモデルを当てはめる（回帰）をしたいモチベーションは様々あるとは思います。

データが無い（$x=3$あたり）の$y$の値を予測したい。とか
データ全体に言える傾向（傾きや切片）を端的に要約したい。とか

では、このデータに対して、モデルを当てはめてみましょう。
モデルというと難しく聞こえますが、要は中学校で習う

y = ax+b

です。

モデルをあてはめてみる

下記式を使って、

y = ax+b

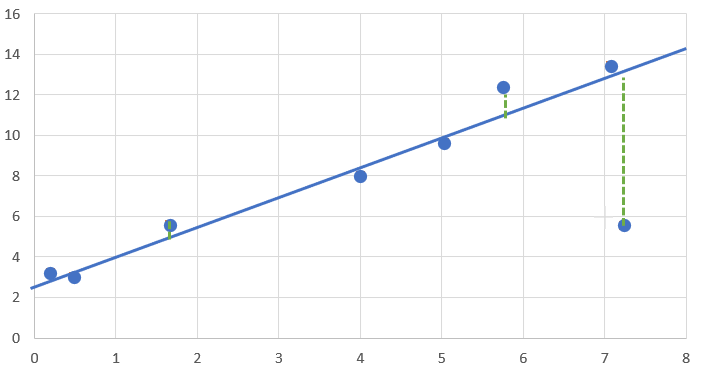
上記データに一本だけ直線を引いてください。と言われると、こんな感じになるかと

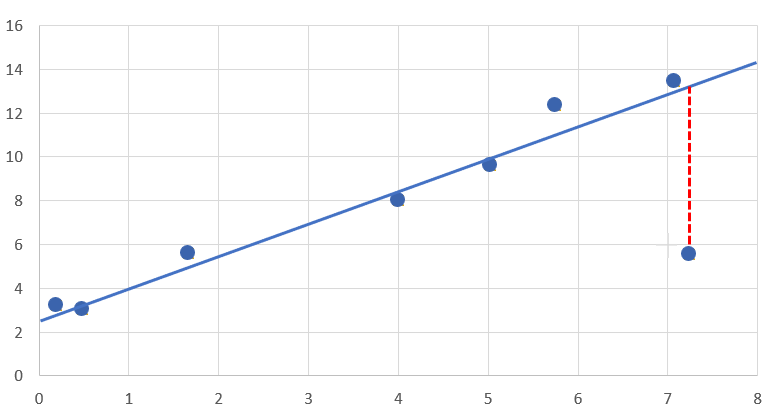
これで、上記のモチベーションを満足することができました。

データが無い（$x=3$あたり）の$y$の値は、きっと$7$くらいかな。
全体的な傾向は、全データを羅列すること無く、$傾き:1.5、切片:2.4$と表現できます。

確かに、赤い破線で示される回帰直線で吸収しきれず残ってしまった差（残差）の部分は気になります。が、全体として 回帰直線がデータに十分に当てはまっているので、下記メリットを享受するため残差は我慢しましょう。

データを十分に要約できた（$傾き:1.5、切片:2.4$）
未知のデータも予測できる（$x=3のとき、きっと、\hat{y}=7$）

といった発想で、データにモデルを当てはめる。これが回帰分析です。
では、この当てはまりの良さはどういった表現が適切でしょうか？
この表現について「意地悪モデル」と「通常モデル」というものを使って理解を進めたいと思います。

意地悪モデル

切片だけモデル

上記では、$\color{red}{a:傾き}、\color{blue}{b:切片}$と２つの変数を調整し、当てはまりのよい回帰直線を検討しました。

y = \color{red}{a}x+\color{blue}{b}

では、ちょっと意地悪な状況を考えてみましょう。

$\color{blue}{b:切片}$だけが調整が可能です。当てはまりの良い直線を引いてもらえませんか？
と言われたらどうするでしょうか。数式で表現するとこんな状況です。

y = \color{blue}{b}

別の見方をすると、$\color{red}{a:傾き}が0$に固定されているとも読み取れるので、下記と表現もできます。

y = \color{red}{0}x +\color{blue}{b}

データにモデルをあてはめてみる

$\color{blue}{b:切片}$だけが調整できるとしたら、与えられた全データに当てはまりのよい$b$はどんな値でしょうか。
$b$が大きすぎても、小さすぎてもデータとの間に、赤破線（残差）が出てしまいます。
そこで、$b$=平均値としたら良さそうでは、ないでしょうか？

y = b
\ \ \ \ \ 
で
\ \ \ \ \ 
\color{blue}{b=8.2}（平均値）
\ \ \ \ \
つまり
\ \ \ \ \
y = \color{blue}{8.2}（平均値）

通常のモデル

では、意地悪モデルから通常のモデルに話を戻しましょう。
通常とは、冒頭に挙げた、下記の式でこの直線がデータに当てはまるように2つの変数を調整します。

y = \color{red}{a}x+\color{blue}{b}

具体的には、$\color{red}{a:傾き}=1.5、\color{blue}{b:切片}=2.4$にすると、下記の様なグラフとなります

上記の、「意地悪モデル」に比べて、随分マシになった気がしませんか？（これが重要）

この、「マシになったな～」を表現するのが「決定係数R2」です。

決定係数R2

「意地悪モデル」と「通常モデル」でみる決定係数R2

冒頭難しい式をとりあげました。今なら、イメージで理解することができます。

R^2 = 1 - \frac{\displaystyle\sum_{i=1}^{n}( y_i - \hat{y_i})^2}{\displaystyle\sum_{i=1}^{n}(y_i - \overline{y})^2} = 1-\frac{残差変動}{全変動}

上記の式の、２乗とかを一旦忘れると¹、この式は、通常モデル vs 意地悪モデルを表す

ということです。

もうちょっと詳しく見てみると

R^2 = 1 - \frac{\color{red}{傾きa}と\color{blue}{切片b}が使える、通常モデルの残差}{\color{blue}{切片b}しか使えない、意地悪モデルの残差}

ということです。例を挙げて見ていきましょう。

傾きaの導入が効果的な場合

$\color{blue}{切片b}$しか使えない、意地悪モデルでは、残差が大きかった。例：残差100
$\color{blue}{切片b}に加え、\color{red}{傾きa}$も使える、通常モデルでは、残差がとても小さくなった。例：残差10

このように傾きaを導入することにより残差が劇的に減る時、決定係数を（ざっくり）¹計算すると

R^2 = 1-\frac{10}{100} = 0.9

よって、$\color{red}{傾きa}$導入の残差改善効果が高い時、決定係数は大きくなります

傾きaの導入が効果的でない（意地悪モデルと結果が変わらない）場合

$\color{blue}{切片b}$しか使えない、意地悪モデルでは、残差が大きかった。例：残差100
$\color{blue}{切片b}に加え、\color{red}{傾きa}$も使える、通常モデルでも、残差は大して変わらず。残差例：残差90

このときは¹

R^2 = 1-\frac{90}{100} = 0.1

となります。
よって、$\color{red}{傾きa}$導入の残差改善効果が低い時、決定係数は小さくなります

まとめ

というわけで、線形回帰と決定係数R2について中学数学で説明をしてみました。
決定係数の数式のこころ理解いただけたでしょうか？言葉でまとめてみると、

「意地悪モデル」（常に平均値）と比較し、傾きの導入でどれだけ「当てはまりが良くなったか」

もっというと、

回帰モデルにおける$\color{red}{傾きa}$の価値や表現力の強さ

を表す指標ということができると思います。
わかりやすさを優先したため、多少冗長になりましたが、お付き合いいただき有りがとうございます。

残差は、プラス方向にも、マイナス方向にも発生するためそれが相殺されないように、２乗をとって絶対値相当（数直線上の原点0からその数値までの距離）を計算しています。 ↩

中学数学で理解する 決定係数r2