「サイトウの代表は、斎藤なのか？」を科学する

サイトウ問題

• みなさんの近くには、「サイトウ（斎藤さん）」はいらっしゃるでしょうか？
• そのサイトウさん、「斎藤」「齋藤」「斉藤」「齊藤」。どの字でしょうか？
• そう！どの漢字だったか忘れてしまう。通称、「サイトウ問題」です。

なにをやるか

• いっそのこと、代表のサイトウを１字決めて、その字に統一できれば、、とか考えました。
• 漢字のカタチから代表のサイトウ を検討する過程を、ネタ的にお送り致します。
• 次元圧縮（UMAP）とクラスタリング（主にKMeans）を用いていきます。
• GW@外出自粛の自由研究。ネタです。ネタです。もう一度言います。ネタです。

漢字として認められている「斎藤」

• ４種（新字体２つ、旧字体２つ）です。東洋経済オンラインによると、
  • ①斎藤が、源流、
  • ②齋藤は、源流(①)の旧字体。
  • ③斉藤は、新字体(①)の書き間違い。　（驚愕の事実　その１）
  • ④齊藤は、旧字体(②)の書き間違い。　（驚愕の事実　その２
• 下記、カッコ内の日本における人口は、①が一番多く、斎藤が源流　である点が感じられる。

	新字体	旧字体
源流	①U+658E (542,000人) 源流	②U+9F4B（86,800人） 源流(①)の旧字体
実は、 書き間違い	③U+6589（323,000人） 源流(①)の書き間違い	④U+9F4A（37,300人） 旧字体(②)の書き間違い

で、気持ち的には

やはり、「斎」（①源流）が、全サイの字（４種）の 代表（ど真ん中） にあってほしい。

なので、確認してみる

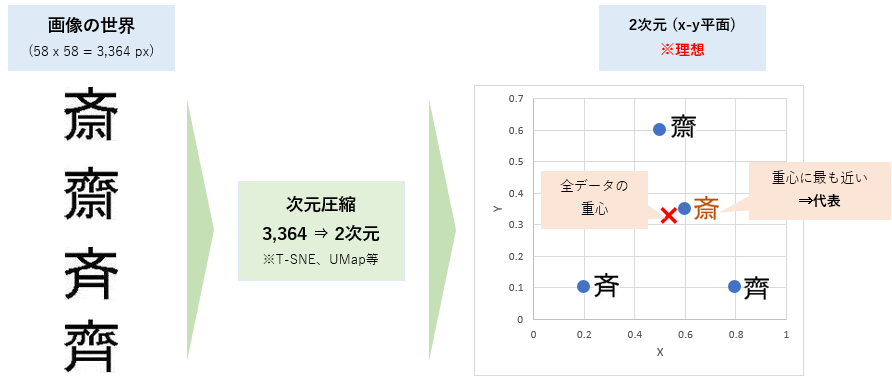
• サイトウの、代表（ど真ん中） を確認するために、サイトウ地図を作りたい。
• 一方、利用画像は、58x58=3,364ピクセル（3,364次元）で、X-Y座標（2次元）にはマッピングできない。
• そこで、次元圧縮という手法を使って、3,364次元　⇒　2次元 に圧縮をしてみたいと思います。
  • 文字の次元圧縮については、こちらの記事で取り上げられているので、リンクさせていただきます。
  • 今回は、次元圧縮のアルゴリズムとして、UMAPを利用します

• では、UMAPで次元圧縮しておきます。

from umap import UMAP
# Umap decomposition
decomp = UMAP(n_components=2,random_state=42)
# fit_transform umap(サイトウ４文字データ)
embedding4 = decomp.fit_transform(all.T[[1,12,31,32]])

検証1) ４つのサイトウの代表を決める

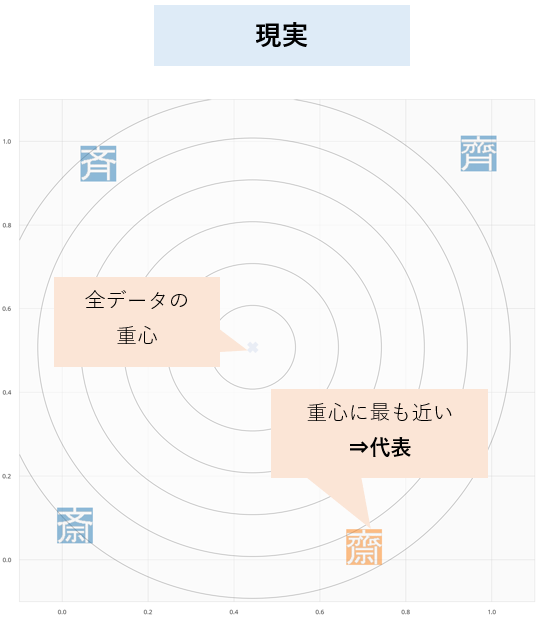
• UMapを利用して、**2次元（平面）に、漢字画像をマッピングし、「代表」**を確認していきます。
• 「中心」(0.5, 0.5)ではなく、全データに対する 「重心」を「代表」 として、見ていきます。
• 「重心」は、xマークで表していますが、いかがでしょう。。（重心 x の下方ですね。）

from sklearn.cluster import KMeans

# clustering（クラスタ数１）
clustering = KMeans(n_clusters=1,random_state=42,)
# fit_predict cluster
cl_y = clustering.fit_predict(embedding4)

# visualize (実装は後述)
showScatter(
    embeddings    = embedding4,
    clusterlabels = cl_y,
    centers       = clustering.cluster_centers_,
    imgs          = all.T[[1,12,31,32]].reshape(-1,h,w)
)

• 微妙ですね、、
  • 「重心」から「各文字」へのユークリッド距離を計算するとこんな感じ。
  • この結果では、②源流（旧字体）の齋 が代表となってしまった。。

重心からの近さ順	文字	重心からの距離	メモ
１位		0.6281	②源流（旧字体）
２位		0.6889	③間違い（新字体）
３位		0.7339	①源流（新字体）
４位		0.8743	④間違い（旧字体）

検証2) 33個のサイトウの「代表」を決める

ところで、サイトウは、何種類あるのか？

• 漢字としては４種類だけだが、実を言うとwikipedia によれば、
• 「斉、斎」以外の異体文字は31パターンもある。
• 一方で、法務省が認めているサイの字は、「斎、齋、斉、齊」の４つだけ。
• つまり、全33パターンのうち、漢字として認められているのは４つだけ
• 漢字として認められているサイトウ以外に、全33サイトウの「代表」 を見てみたい

• では、今度は33文字分UMAPで次元圧縮しておきます。

from umap import UMAP
# Umap decomposition
decomp = UMAP(n_components=2,random_state=42)
# fit_transform umap(全33文字データ)
embeddings = decomp.fit_transform(all.T)

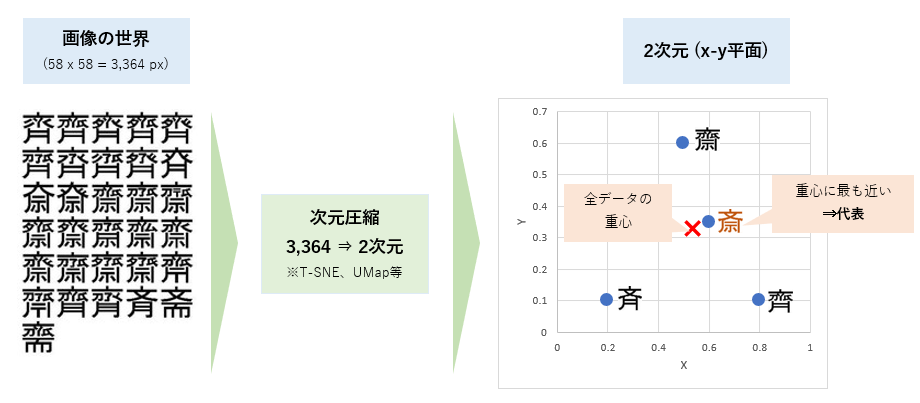
33個の「サイトウ」の「代表」は？

• 同じくUMAPで次元圧縮し、「重心」に近い漢字を確認していきます。

from sklearn.cluster import KMeans
# clustering(クラスタ数 : 1)
clustering = KMeans(n_clusters=1, random_state=42)
# fit_predict cluster
cl_y = clustering.fit_predict(embeddings)
# visualize
showScatter(embeddings, cl_y, clustering.cluster_centers_)

期待していた、「斎」 ではなく、 が、代表（ど真ん中）に近い結果となってしまいました。。

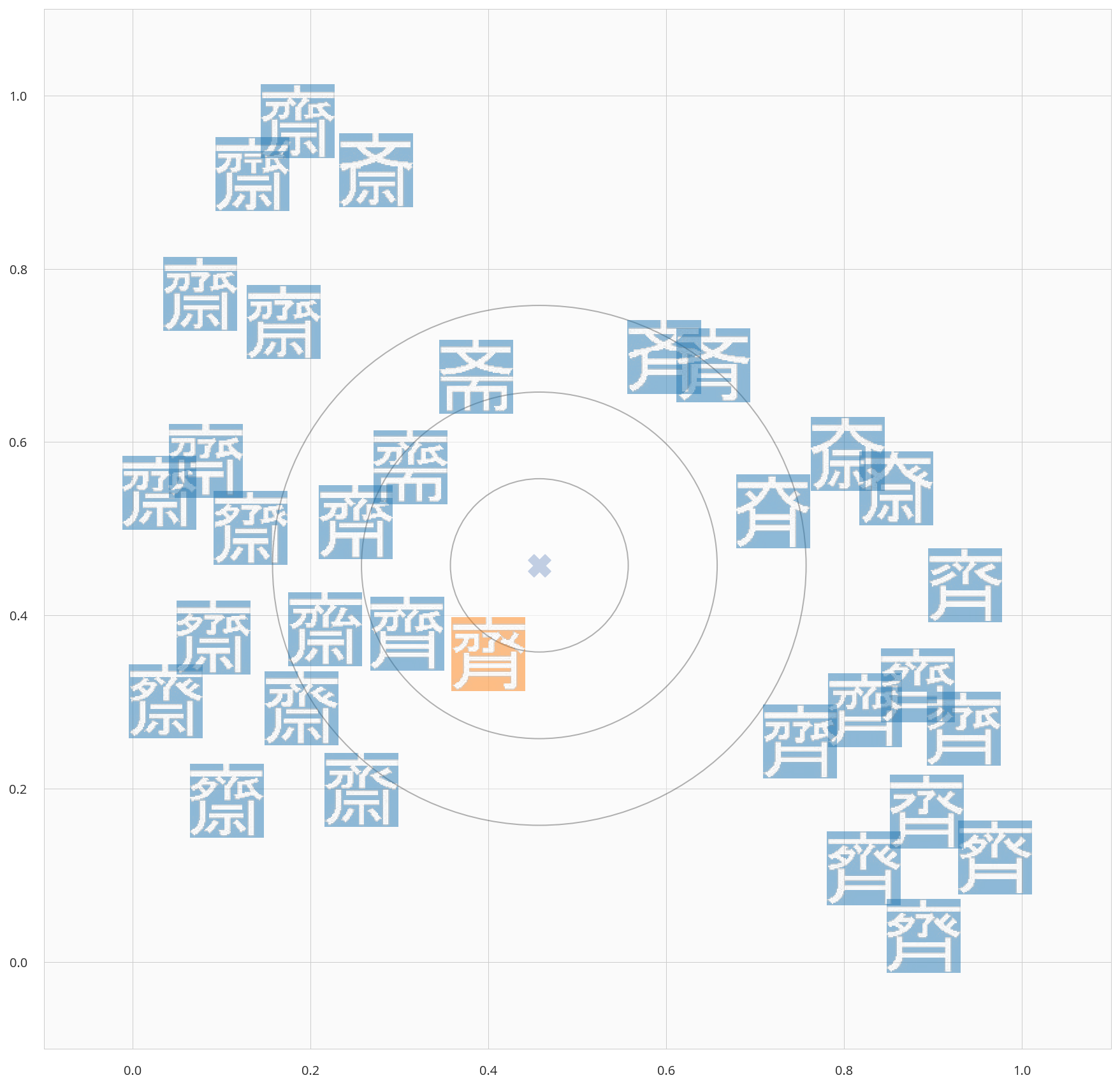
• 重心からの距離順（上位）は以下の通り。なかなか期待通りには行かないｗｗ

重心からの近さ順	文字	重心からの距離	メモ
１位		0.494
２位		0.787
３位		1.013
４位		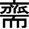1.014

検証3) 代表の「サイトウ」を４文字選ぶ

• 「ど真ん中」はうまく行かなかったのですが、漢字として認められているのは、４種類。
• では、この地図上の漢字を４クラスタに分離して、それぞれのクラスタの重心はどの漢字となるか？
• つまり、全33字から、代表の4字 を選んで見たいと思います。
• クラスタリングアルゴリズムのKMeansを利用し、4クラスタに分離すると下記のとおり。

from sklearn.cluster import KMeans
# clustering(クラスタ数 : 4)
clustering = KMeans(n_clusters=4, random_state=42)
# fit_predict cluster
cl_y = clustering.fit_predict(embeddings)
# visualize
showScatter(embeddings, cl_y, clustering.cluster_centers_)

• 各クラスタの文字と重心に近い文字は下記の通り。
• なんとなく漢字の特徴（月や示）を捉えたクラスタにはなっていそう。
  • クラスタ重心の近傍点がクラスタの特徴を捉えられているか？は微妙。
  • ４クラスタだと分類しきれず、赤クラスタは複数のパターンを含む。
  • もう少し、細かく分類する必要がありそう
• ざっくり見てみると、倍の８クラスタあれば、キレイに分けられそうな予感。

No	クラスタ	重心	他に含まれる字
1	赤
2	橙
3	青
4	緑

検証4) ８クラスタ化してみる

• 先程は、代表の漢字を４文字選ぶために４クラスタでした。
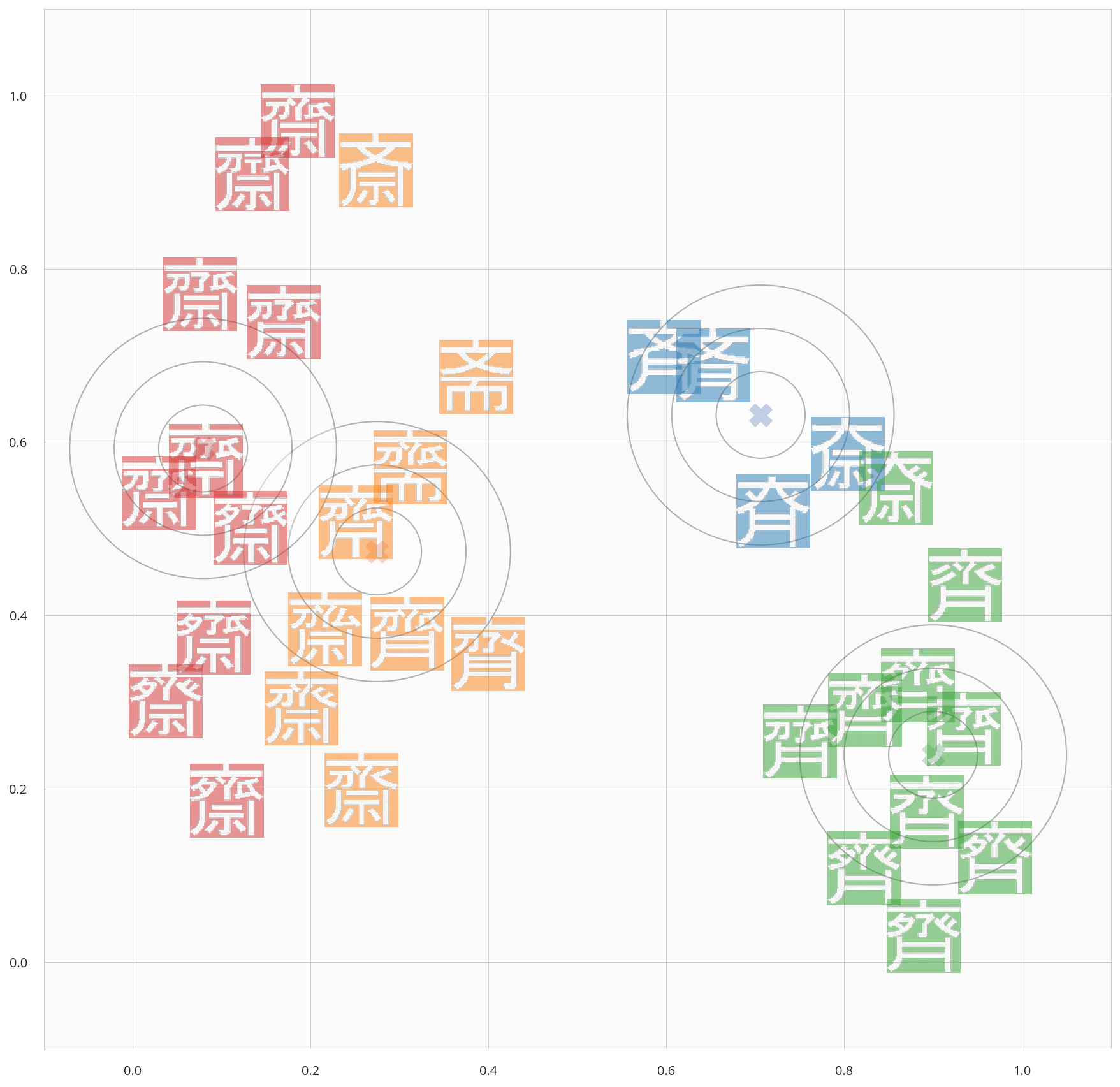
• ただ、結果を見ると、キレイに分離できていないクラスタも存在したので、クラスタ数を８にしてみます。
• 結果は下記の通り。

from sklearn.cluster import KMeans
# clustering(クラスタ数 : 8)
clustering = KMeans(n_clusters=8, random_state=42)
# fit_predict cluster
cl_y = clustering.fit_predict(embeddings)
# visualize
showScatter(embeddings, cl_y, clustering.cluster_centers_)

• キレイに分離ができているわけではないですが、なんとなく仕分けできた感じです。

No	クラスタ	クラスタに含まれる字
1	桃
2	赤
3	茶
4	灰
5	橙
6	青
7	紫
8	緑

• 惜しいのは、橙の と、灰ので、クラスタが割れてしまっています。
• ただ、両者ともクラスタの境界線上のデータであるため、思いは伝わってきます（笑）
  

検証5) 何クラスタが妥当かを確認する

• 漢字として登録のある４字に合わせて、４クラスタ。
• そして、４クラスタの結果をみて、８クラスタに分離してみたわけですが、、
• 果たして、何クラスタにするのが適切なのでしょうか？
• ここでは、クラスタ数を選定する方法として、下記３手法でクラスタの状態を可視化、検討してみたいと思います。
  1. Elbow Chart
  2. Silhouette Chart
  3. dendrogram

Elbow Chart

• elbow chartは縦軸に 各クラスタでのデータのばらつき 、横軸に クラスタ数 をとった図です。
• クラスタの数を多くすれば、ばらつきを抑えることが出来ますが、クラスタ数が多すぎるのも問題です。
• そこで、そこそこのクラスタ数 でかつ データのばらつきも抑えられる クラスタ数をこの図で検討します。
• 作図には、Yellowbrickを利用していきます。

from yellowbrick.cluster import KElbowVisualizer
vis = KElbowVisualizer(
    KMeans(random_state=42),
    k=(1,34) # クラスタ数（横軸の範囲)
)
vis.fit(embeddings)
vis.show()

• 見ている感触では、
• クラスタ数５までは、順調に データのばらつき（の平均）は下がり が、以降はフラットに。
• よって、５クラスタに分類 が良さそう　＝　代表の漢字は ５種 が良さそうです。
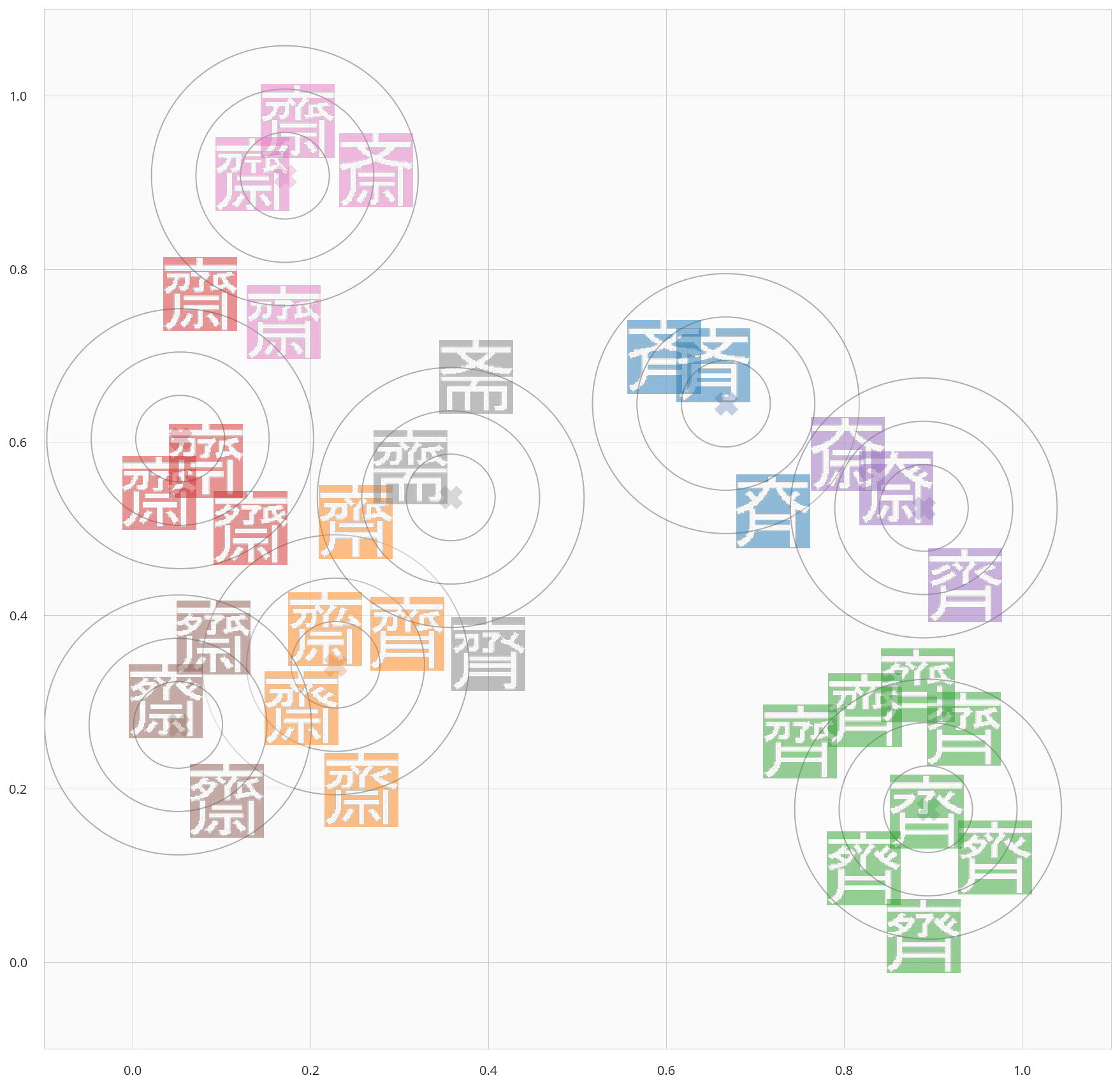
• が、一応拡大版も見ておきましょう（４～１８で拡大）
• ５に変曲点がありそうなのですが、概ね10付近 からフラットになっています。
• つまり、 感覚で８クラスタに分類し、代表漢字を８個決めた のも間違いではなさそうです。

from yellowbrick.cluster import KElbowVisualizer
vis = KElbowVisualizer(
    KMeans(random_state=42),
    k=(4,19) # クラスタ数（横軸の範囲)
)
vis.fit(embeddings)
vis.show()

Silhouette Chart

• Silhouette Chartは、クラスタ毎に下記を表現した図です。
  • 縦軸（グラフの厚み）　：　そのクラスタのサンプル数
  • 横軸（グラフの長さ）　：　そのクラスタのシルエット係数
  • 破線　：　シルエット係数の平均
• 見方としては、下記を満たすようなグラスタ数を見つけるのがポイントです。
  • どのクラスタも同じサンプル数　＝　厚みが一緒
  • どのグラスタもシルエット係数が平均に近い　＝　長さが破線に近い
• 作図には、同じくYellowbrickを利用していきます。

from yellowbrick.cluster import silhouette_visualizer
fig = plt.figure(figsize=(15,25))
# クラスタ数4～9までまとめて作図
for i in range(4,10):
    ax = fig.add_subplot(4,2,i-1)
    silhouette_visualizer(KMeans(i),embeddings)

• 見る感じでは、右上（クラスタ数５）のパターンがいい感じです。

dendrogram

• クラスタ同士の 近さ をトーナメント表の様に表現したグラフです。
• 階層型クラスタリングで利用できる図ですので、KMeansでなく、Scipyの階層型クラスタリングを使っています。
• 見方としては、下記です。
  • 葉がデータで、同じ色の枝の範囲が同じクラスタ
  • 高さが、クラスタ間の距離

from scipy.cluster.hierarchy import linkage, dendrogram
Z = linkage(
    y = embeddings,
    method = 'weighted',
    metric = "euclidean",
)

R = dendrogram(
    Z=Z,
    color_threshold=1.2, #この閾値でクラスタ数を調整
    show_contracted=False,
)

• 各色の枝の数がバランスよく、高さも揃っていると いい感じです。やはり、クラスタ数は５程度でしょうか。

クラスタ数	デンドログラム	コメント
４		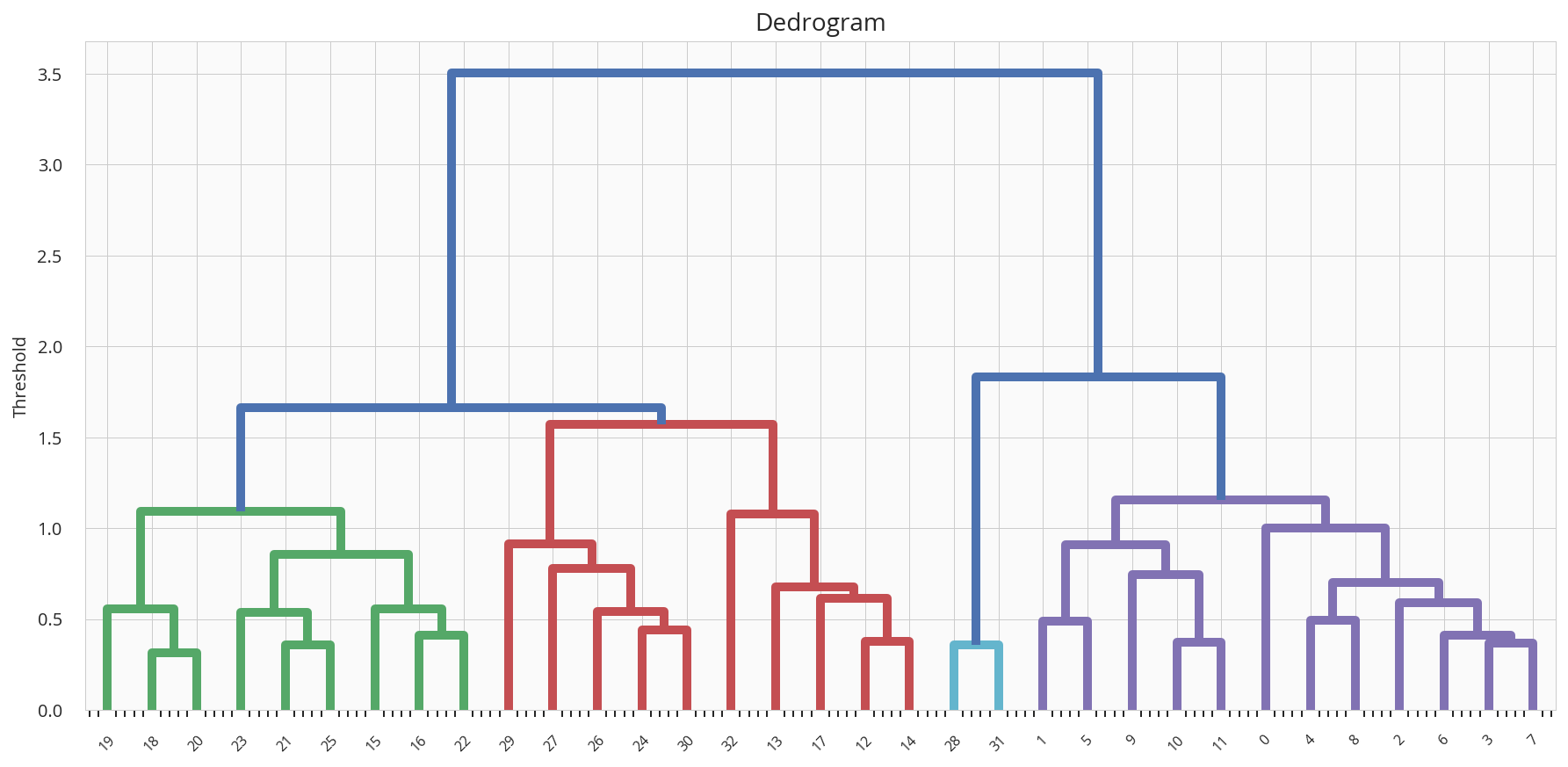赤だけ、少し高い
５		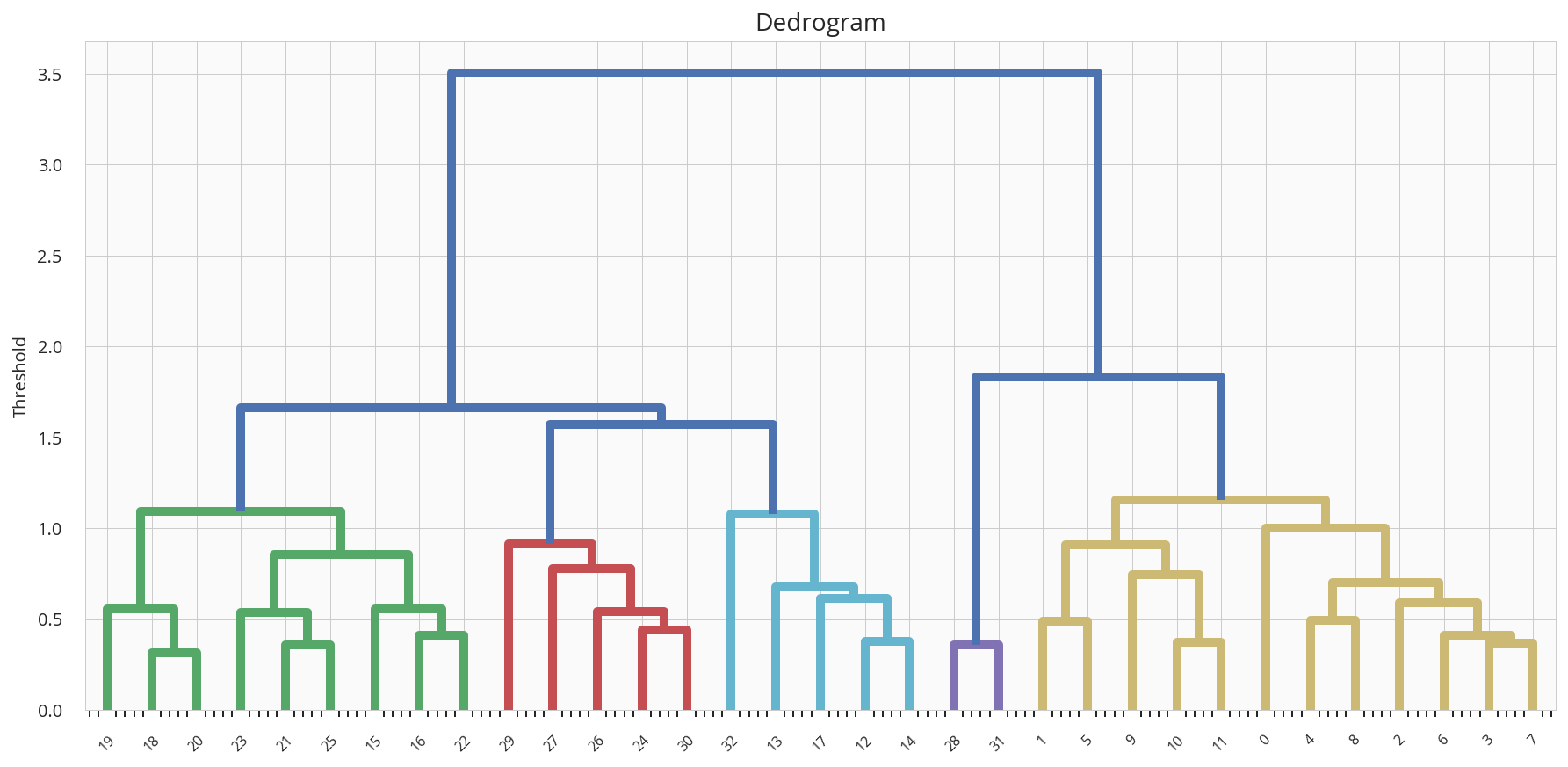高さは揃っている 紫の少数が気になるが なかなかいい感じ
８		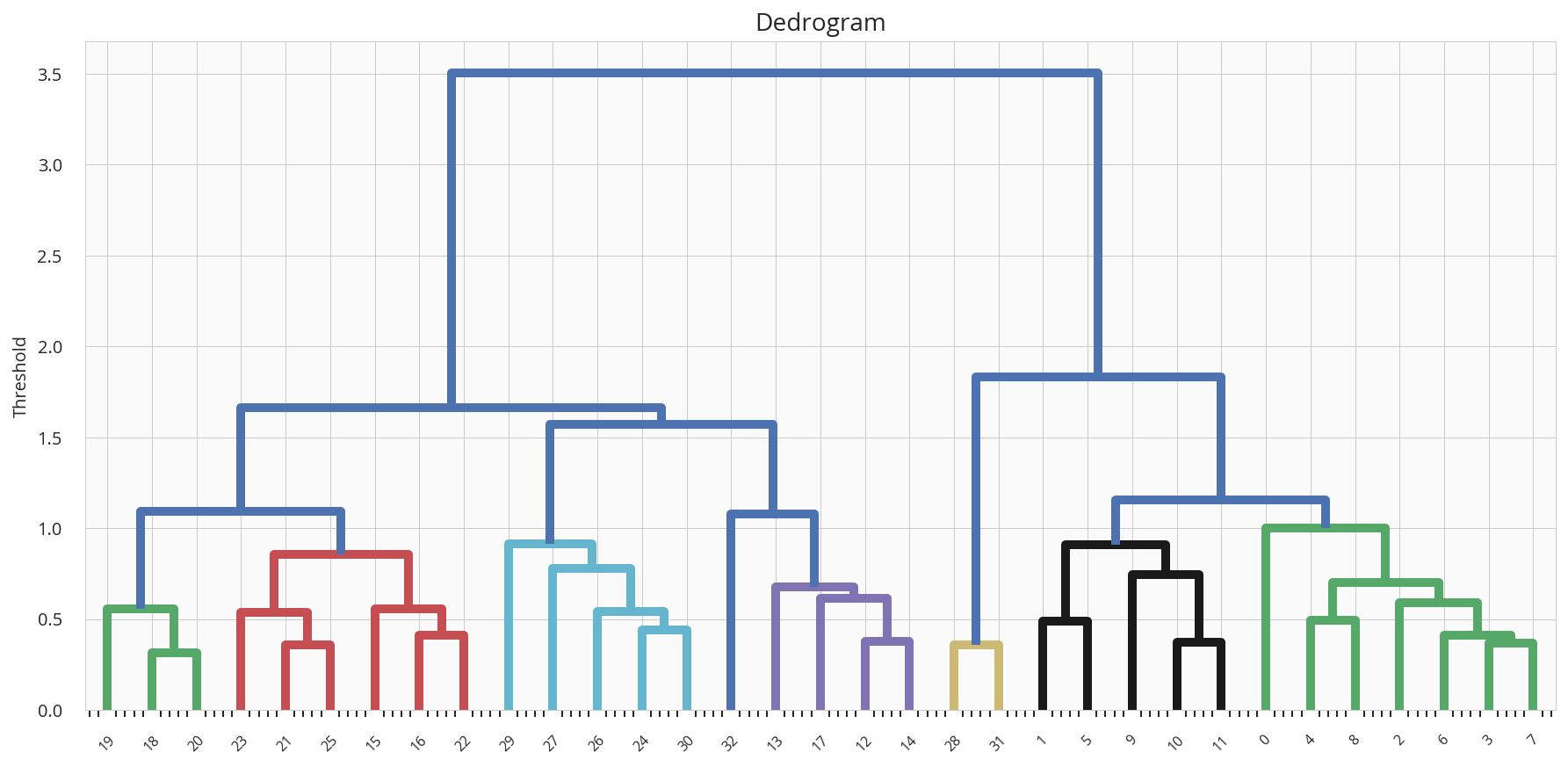高さ、数も揃っているが、 細かく分割しすぎか

検証6) ５クラスタにしてみる

• クラスタ数を検討してみたので、再び、５クラスタでどんな感じになるかプロットしてみたいと思います。
• なかなか良さそうですね。やはり、５クラスタでしょうか。

from sklearn.cluster import KMeans
# clustering(クラスタ数 : 5)
clustering = KMeans(n_clusters=5, random_state=42)
# fit_predict cluster
cl_y = clustering.fit_predict(embeddings)
# visualize
showScatter(embeddings, cl_y, clustering.cluster_centers_)

No	クラスタ	重心	他に含まれる字
1	青
2	紫
3	緑
4	赤
5	橙

まとめ

所感

• 流れとしては、
  • 漢字として登録されている４文字の代表選びからスタートし
  • 漢字として登録のない全３３字については、１，４，８文字を選び
  • 適切なクラスタ数を検討し、５クラスタが良さそうということで、最後に５文字選びました
• 代表漢字は下記となるわけですが、代表を決める以上に
  • 3000次元を次元圧縮したXY平面上で、カタチの似た漢字は近傍に配置される点も興味深いですし
  • 距離ベースのクラスタリングで、部首毎のグループが作れることは興味深かった
  • クラスタ数の検討も、エルボー法、シルエット法、デンドグラムでの検討結果で５クラスタと判断し
  • ５クラスタのクラスタリング可視化の結果もそこそこしっくりくる点も面白かったです。

検証一覧

No	選び方	代表のサイトウ たち
1	認められた４漢字から １字選ぶなら代表は
2	全33漢字から １字 選ぶなら
3	全33漢字から ４字選ぶなら
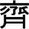
4	全33漢字から ８字選ぶなら
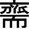
5	全33漢字を 何クラスタに分けるべきかは	５クラスタ程度 が良さそう
6	全33漢字から ５字選ぶなら

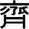
最後に

• こんなくだらないネタにお付き合い頂きありがとうございました。
• よろしくければ、いいね、シェアしていただければ嬉しいです。

参考情報

• UMAPについて
  • https://umap-learn.readthedocs.io/en/latest/index.html
• UMAPでのClusteringについての議論（があるようです）
  • https://umap-learn.readthedocs.io/en/latest/index.html
• KMeansについて
  • https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
• クラスタ数の検討について(YellowBrick)
  • https://www.scikit-yb.org/en/latest/api/cluster/elbow.html
  • https://www.scikit-yb.org/en/latest/api/cluster/silhouette.html
• デンドログラムでの作図
  • https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.cluster.hierarchy.dendrogram.html

可視化関数

• こちらの記事を参考にさせていただきました。ありがとうございます。リンクさせていただきます。

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
from matplotlib import offsetbox
from sklearn.preprocessing import MinMaxScaler
from PIL import Image
import matplotlib.patches as patches

rc = {
  'font.family': ['sans-serif'],
  'font.sans-serif': ['Open Sans', 'Arial Unicode MS'],
  'font.size': 12,
  'figure.figsize': (8, 6),
  'grid.linewidth': 0.5,
  'legend.fontsize': 10,
  'legend.frameon': True,
  'legend.framealpha': 0.6,
  'legend.handletextpad': 0.2,
  'lines.linewidth': 1,
  'axes.facecolor': '#fafafa',
  'axes.labelsize': 10,
  'axes.titlesize': 14,
  'axes.linewidth': 0.5,
  'xtick.labelsize': 10,
  'xtick.minor.visible': True,
  'ytick.labelsize': 10,
  'figure.titlesize': 14
}
sns.set('notebook', 'whitegrid', rc=rc)

def colorize(d, color, alpha=1.0):
  rgb = np.dstack((d,d,d)) * color
  return np.dstack((rgb, d * alpha)).astype(np.uint8)

colors = sns.color_palette('tab10')

def showScatter(
    embeddings,
    clusterlabels,
    centers = [],
    imgs = all.T.reshape(-1,h,w),
):
    fig, ax = plt.subplots(figsize=(15,15))
    
    #散布図描画前にスケーリング
    scaler = MinMaxScaler()
    embeddings = scaler.fit_transform(embeddings)
    
    source = zip(embeddings, imgs ,clusterlabels)
    
    #漢字を散布図に描画
    cnt = 0
    for pos, d , i in source:
        cnt = cnt + 1
        img = colorize(d, colors[i], 0.5)
        ab = offsetbox.AnnotationBbox(offsetbox.OffsetImage(img),0.03 + pos * 0.94,frameon=False)
        ax.add_artist(ab)
          
    #重心からの同心円を描画
    if len(centers) != 0:
        for c in scaler.transform(centers):
            for r in np.arange(3,0,-1)*0.05:
                circle = patches.Circle(
                    xy=(c[0], c[1]),
                    radius=r,
                    fc='#FFFFFF', 
                    ec='black'
                )
                circle.set_alpha(0.3)
                ax.add_patch(circle)

            ax.scatter(c[0],c[1],s=300,marker="X")
  

    # 軸の描画範囲
    limit = [-0.1,1.1]
    plt.xlim(limit)
    plt.ylim(limit)
    plt.show()