PyCaretにてモデルを較正(Calibration)する

はじめに

• ２値分類等した際に、しきい値を決めPos/Negを分類するのは良いとして、、
• モデルの出力値を、Positiveとなる確率として見なしてよいか？は別問題となります。
• 上記を行いたい場合には、モデルによっては較正（Calibration）をする必要があります。
• この較正（Calibration）をPyCaretを使って行ってみたいと思います。

モデルを作る

• PyCaretのチュートリアルに従い普通に決定木でモデリングしていきます。
• データセットとして、 diabetes（糖尿病）データセットを利用します。

データのロード

from pycaret.datasets import get_data
diabetes = get_data('diabetes')

決定木を使ってモデリング

• 分類をしたいので、pycaret.classificationをインポートします。
• そして、create_modelでdt(決定木)を指定すればモデリングできます。
• できたモデルはevalutate_modelで観察してみます。

# 分類パッケージをインポート
from pycaret.classification import *
clf1 = setup(data = diabetes, target = 'Class variable')

# 決定木を作る
dt = create_model(estimator='dt')

# 可視化
evaluate_model(dt)

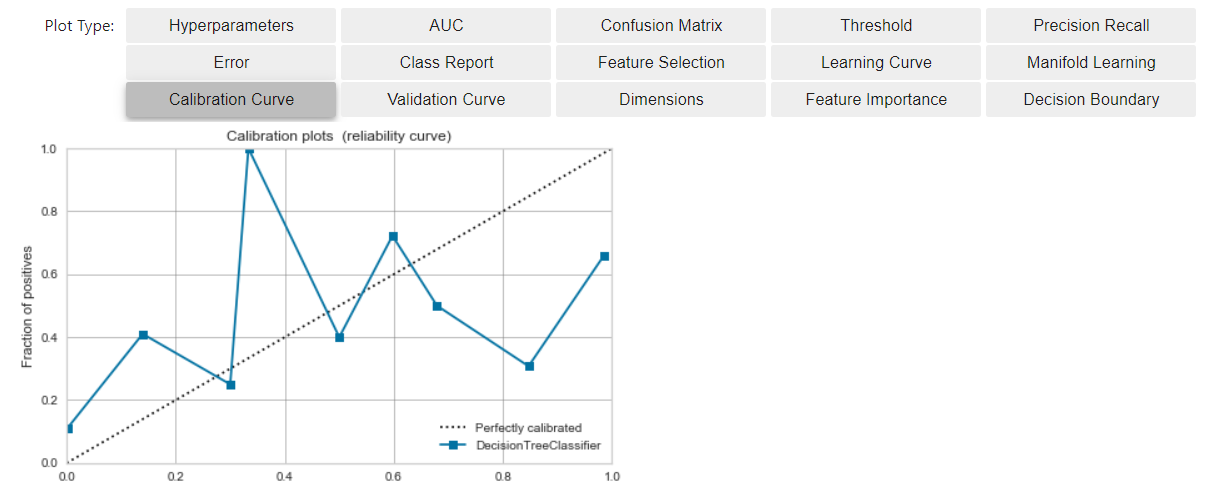
較正前のCalibration Curveを確認

• 下記ボタンで、Calibration Curveを確認できます。
  • 横軸は、モデルのスコアリング結果をビニングし、値順に並べたモノ
  • 縦軸は、そのビンまでに出現した、Positiveデータの割合
• 理想的な状況（※）では、
  • モデルの出力値に対してバランス良くPositiveデータが出現するので、
  • モデル（青線）が、斜めの理想線（破線）に近づきます

モデルを較正する(Calibration)

• Calibrationは、現状のモデルを上述（※）の状況に近づける作業です。
• ※の状況に近づけることにより、モデル出力値を、予測結果がPositiveである確率と見なしやすくなります。
• 実施方法は簡単で、calibrate_modelを使います。

# calibrationする
calibrated_dt = calibrate_model(dt)

# 可視化する
evaluate_model(calibrated_dt)

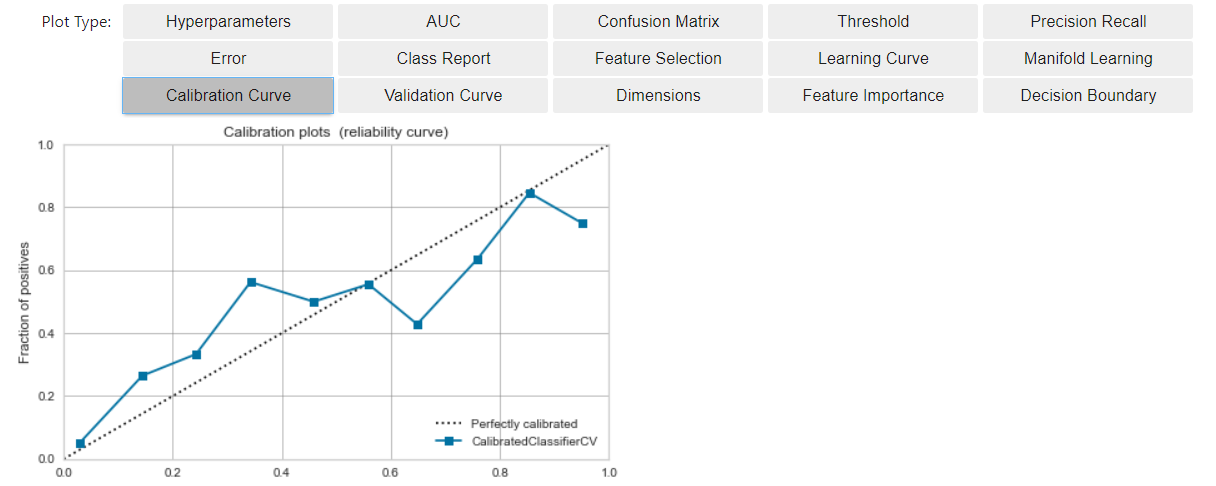
• 先程に比べ、理想線（破線）にモデル（青線）が近づいた状況になりました。
• モデルのスコアリング結果に対して、
• その時点でのPositiveの累積出現割合が線形増加する（※に近い状況）を作ることができました。

較正は何で実現されているか？

• sklearn.calibration.CalibratedClassifierCVを利用している様です。
• sklearnは較正の手法として'sigmoid'と'isotonic'に対応していますが、pycaretでも同様のドキュメンテーションとなっています。

どのモデルが較正が必要"そうか？"

• SVMはマージン最大化の為、決定境界周辺を厳しく確認する関係でモデル出力値が0.5に集中し較正が必要。という点はこちらの記事で論じられていますが、他はどうでしょうか？

• どのモデルで較正が必要かの厳密な議論は、専門家にまかせて、本記事では、較正前後のCalibration Curveを書いてみてどういった傾向があるかを観察してみたいと思います。

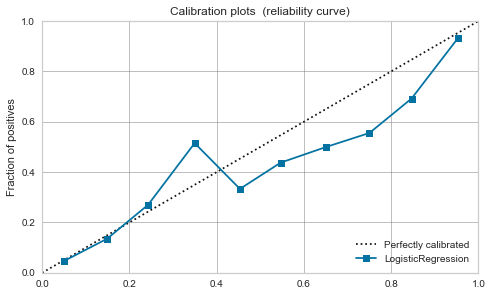
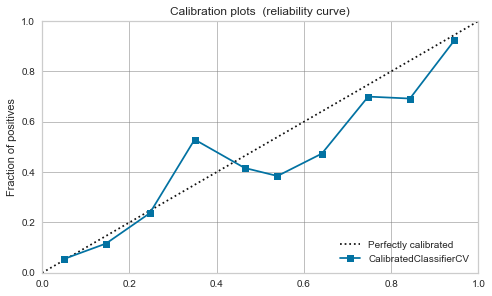
• ロジスティック回帰

  • 元々、Positiveの確率として解釈可能なので較正前からバランス良いです。
  • 較正後もあまり変わらないですね。

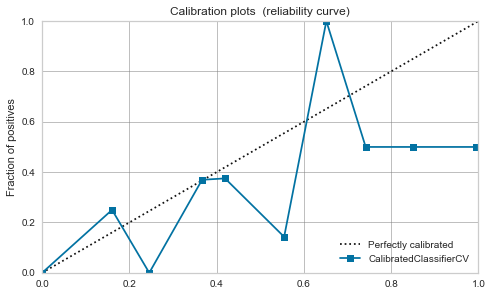
• RBFカーネルSVM

  • 激しいですね。上記記事の通りマージン最大化で0.5付近にデータが寄る様です。
  • 較正してもあまり改善せず、モデル出力値を確率と見なし扱うのは危なそうです。

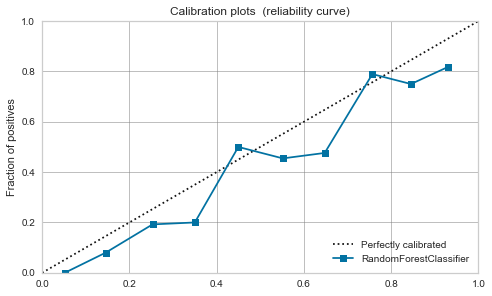
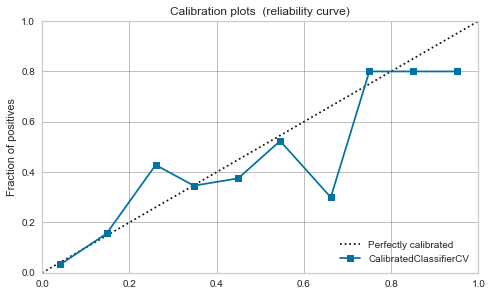
• ランダムフォレスト

  • 較正前から、ある程度バランスは良さそうです。
  • 今回は較正により、0.7あたりにピークが出てしまっています。

• XGBoost,LightGBM

  • 較正前でも、そこそこ。較正すれば少し落ち着く。

アルゴリズム	較正前	較正後
Logistic Regression
RBF SVM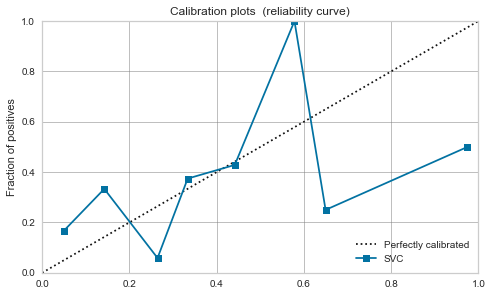
Random Forest
XGBoost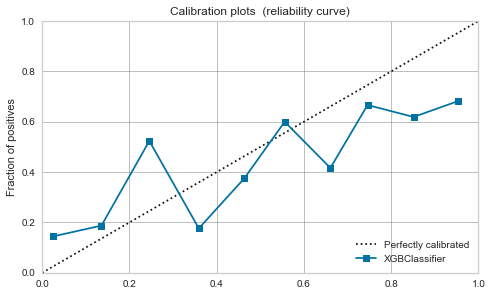
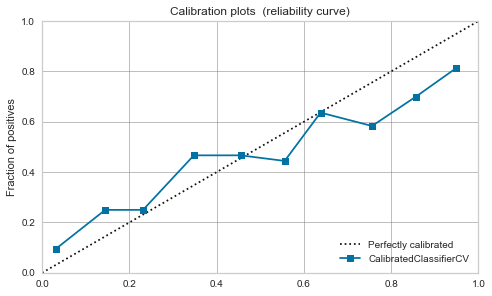LightGBM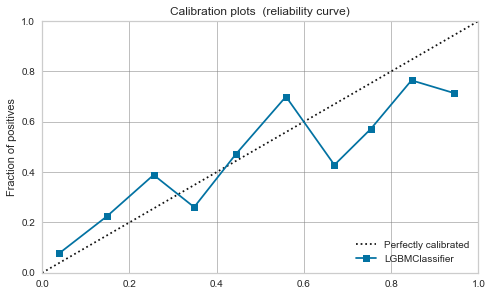

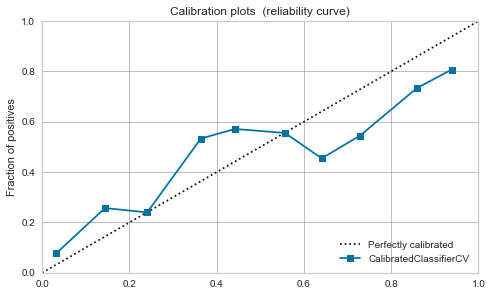最後に

• PyCaretでモデルを較正してみました。
• モデル出力値をPositiveの確率と見なしたい時は、Calibration Curveの確認が必要ですね。
• 較正してもSVMのマージン最大化等、アルゴリズムが元々持つ特性で厳しいこともある。
• ロジスティック回帰のように、較正せずとも確率と見なしやすいモデルもあるので、用途によって使い分けるアプローチもあると思います。

関連記事