Solovay-Kitaevの定理を「見える化?」する

この記事について

量子ゲートのユニバーサルゲートセット（万能ゲートセット）は、

• 1量子系では、$\{H, T\}$
• 2量子系では、上記にCNOTを加えた$\{H,T,CNOT\}$

であることが知られています。
また、
上記ゲートセットにて任意の量子操作を近似する際に、$H,T$が何個程度必要か？
についてはSolovay-Kitaevの定理が必要ゲート数を示しているのですが、難しい内容ですので、

• 本稿では、$H,T$のゲート数を増やしていったときに、
• ブロッホ球上でどの程度の範囲がカバー可能か？

について議論を進めて行きたいと思います。

なお、ユニバーサルゲートセットやSolovay-Kitaevの定理については下記にて詳しく解説されているのでリンクさせていただきます。

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

% basic braket 
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1}  \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1}  \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}

おためし（H、S）

$H,T$ゲートを何個つかうと、ブロッホ球全域の状態のどれくらいの範囲をカバーできるか？
を見ていきたいのですが、これから何をやるかを説明するために、、

まずは、理解のしやすい組み合わせの$\{H,S\}$のゲートセットでの動きを見ていきます。
（なお、$\{H,S\}$はユニバーサルゲートセットでは無いです。）

HとSを計２個つかう

このとき、作成する量子回路で、ブロッホ球のどの範囲を移動することが可能でしょうか？
具体的に見ていきましょう。
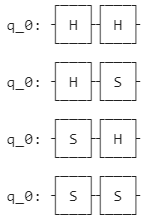
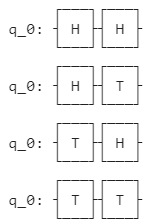
HとSを計２個使うと、作成できる組み合わせは４通りです。（$HH,HS,SH,SS$）
量子回路にすると下記のような状況です。

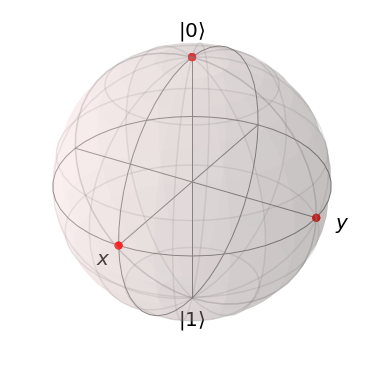
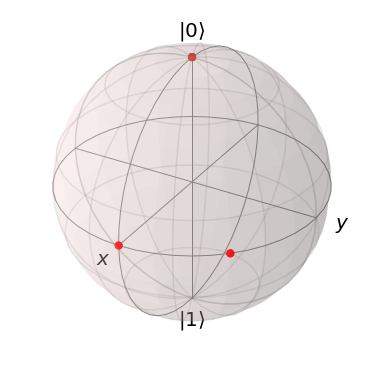
このときに、ブロッホ球上で到達可能な点は、下記の３点です。

理由としては、計算してみれば自明で、到達可能な点は３点です。

\displaylines{
HH\ket{0} \equiv \ket{0}
\ \ \ 
SH\ket{0} \equiv \ket{i}
\\
HS\ket{0} \equiv \ket{+}
\ \ \ 
SS\ket{0} \equiv \ket{0}
}

HとSを計３個つかう

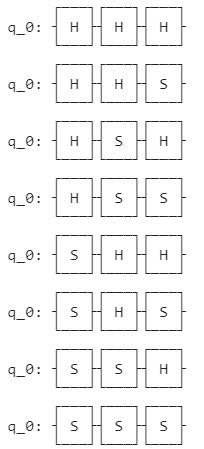
使えるゲートの数を増やしてみましょう。組み合わせは$2^3=8$通りで、下記の通りです。
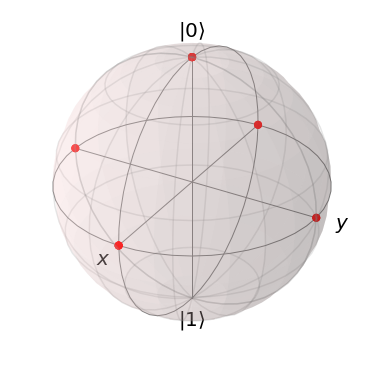
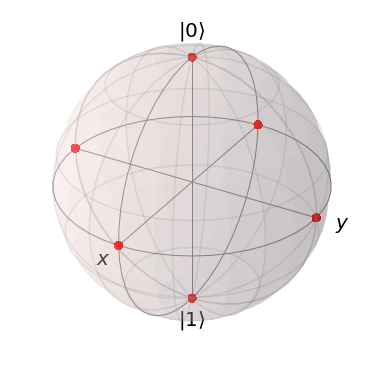
到達可能は点は下記５点です。

確認しておくと、

\displaylines{
HHH\ket{0} \equiv \ket{+}
\ \ \ 
HHS\ket{0} \equiv \ket{0}
\\
HSH\ket{0} \equiv \ket{i-}
\ \ \ 
HSS\ket{0} \equiv \ket{+}
\\
SHH\ket{0} \equiv \ket{0}
\ \ \ 
SHS\ket{0} \equiv \ket{i}
\\
SSH\ket{0} \equiv \ket{-}
\ \ \ 
SSS\ket{0} \equiv \ket{0}
}

HとSを計１０個つかう

一気に、使えるゲートの数を増やしてみましょう。組み合わせは$2^{10}=1024$通りで、
回路としては下記の通りです。（一部抜粋で、掲載します）

雰囲気的に、様々な状態を表現できそうですが、、、
実際には、下記6点（各軸の基底）にしかたどり着くことができないのです。

本題に入ります（H、T）

１量子系のユニバーサルゲートセットの$\{H,T\}$を使うとどれほどの範囲が表現可能でしょうか？
見ていきたいと思います。

HとTを計２個つかう

回路としては、4パターンとなります。

到達可能な状態は、下記の3パターンとなります。
先程試した、$\{H,S\}$と比較すると、$T$は、$\pi/4(45^\circ)$回転ですので、$\ket{0},\ket{+}$以外の３点目ちょうど$45^\circ$の位置に到達しています。

HとTの数を増やしていく

要領は一緒ですので、$\{H,T\}$の数を増やしていくと、到達可能な状態はどの様に増えていくでしょうか？
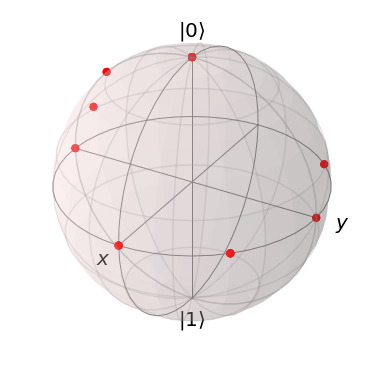
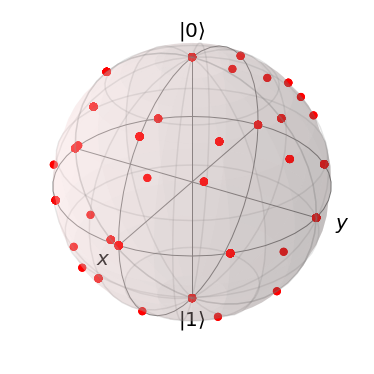
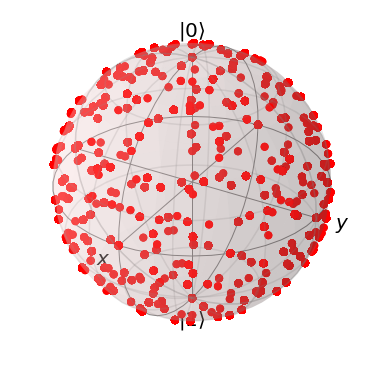
結果は下記の通りで、$\{H,T\}$を16個使うと、回路構成パターンの$2^{16}=65536$通りとは行きませんが、ブロッホ球全域をくまなくカバーできることがわかります。
（誤差$\varepsilon$は残りますが、そこそこの精度で近似できそうです）

	ゲート4個	ゲート8個	ゲート16個
回路	$2^4=16$通り	$2^8=256$通り	$2^{16}=65536$通り
到達 状態

なぜ、{H,S}ではだめで、{H,T}ならよいのか

詳細は、冒頭紹介させて頂いた記事を参照いただきたいのですが、直感的な説明としては、

• $S$の$90^\circ$回転と、$H$を組み合わせても、6箇所しか行き着けない
• $T$の$45^\circ$回転と、$H$を組み合わせると、$H$が**$Z$と$X$の間の$45^\circ$方向を中心した回転**なので、この組み合わせにより、様々な状態にたどり着くことができる。

といった感じで、$H$の回転の詳細は下記参照いただければと思います。

まとめ

厳密性を欠いた、かなり雑な説明になりましたが、ユニバーサルゲートセット$\{H,T\}$を、
そこそこの数用いると、任意の量子状態を一定の誤差の範囲で近似できそう。
といった感覚が伝われば嬉しく思います。
何かあれば、コメント等、よろしければ、LTGM頂ければ嬉しいです。

参考（ソースコード）

• 汚いですが、載せておきます
• なお、ブロッホ球が歪んでしまった方は、下記参照してみてください

描画に利用する関数の準備

from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
from qutip import *
import itertools

# 状態ベクトルをqutipデータに変換
def state_vector2qobj(state_vector):
    return (state_vector[0] * basis(2,0) + state_vector[1] * basis(2,1)).unit()

# 状態ベクトルを計算
def calc_state_vector(gate_str):
    qc = QuantumCircuit(1)
    for gate_char in gate_str:
        method = getattr(qc,gate_char)
        method(0)
    state = Statevector.from_instruction(qc)    
    return state_vector2qobj(state.data)

# 回路のパターンを列挙
def generate_gate_str(repeat=10,gate_sets='ht'):
    ret = list(
        itertools.product(
            gate_sets,
            repeat=repeat
        )
    )
    print("Size of Patterns : " + str(len(ret)))
    return ret

ブロッホ球の描画

b = Bloch(figsize=(5,5))
GATE_LENGTH = 8
GATE_SETS = 'ht'

# 指定されたゲートセット、長さで状態ベクトルを計算
obj_list = [
    calc_state_vector(
            gate_str
    ) for gate_str in generate_gate_str(
        GATE_LENGTH,
        GATE_SETS
    )
]

# qutipに点を打つ
for qobj in obj_list:
    b.add_states(qobj,kind='point')

# 描画
b.point_color = ['r']
b.point_marker = ['o']
b.point_size = [50]
b.show()