イメージでざっくり理解する量子コンピュータ

前置き

ついに、アドベントカレンダーが始まりました！！
量子コンピュータのカレンダを企画し、第１日目はどうしようと悩んでいたのですが、25日を通して幅広い方に読んでほしいので、まずは量子計算のイメージを掴んで頂くことが重要と考えました。
そこで、初日の本日は、

• 量子計算ってなにもの？ かを イメージでご理解いただく記事をご準備しました。
• 量子計算って「そういう雰囲気なのね！」 と言っていただけるように、頑張ります。

最初に、本日の結論をお示しすると、こちらの栗まんじゅうでございます。

注意

超入門を目指すために、理解／イメージ最優先で、正確性をある程度犠牲にし進めます。
なお、筆者の理解が及ばず、正確性を犠牲にしている場合もありますので（笑）、、
その場合はコメントいただけますと幸いです。

量子コンピュータってなに？

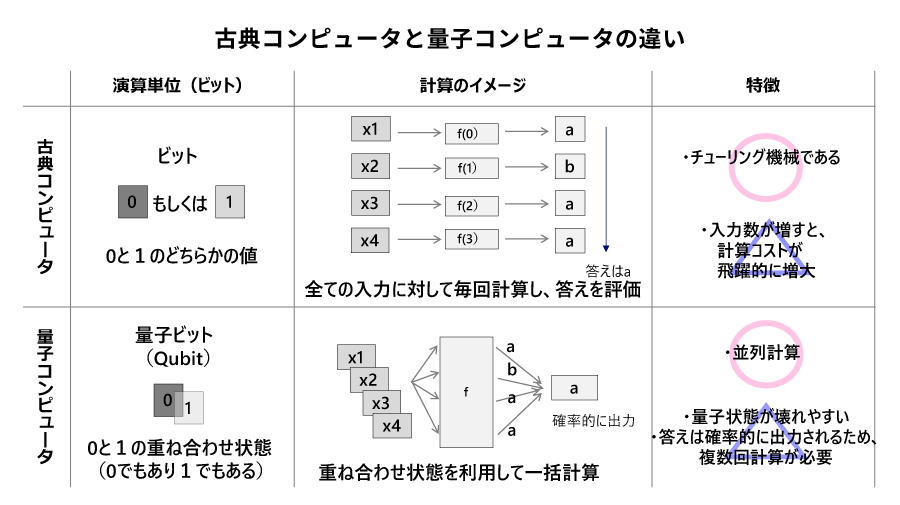
こちらの資料¹で説明を進めて行ければと、

古典コンピュータ

「ふつーの計算機（PC・サーバ）」 は上段の 「古典コンピュータ」 です。
古典というのは、古いとかっていう意味ではなく、、

• 物理学で、「量子力学」登場前の、ニュートン力学等を「古典力学」と呼称します²
• その背景で、量子コンピュータと対比し「古典コンピュータ」と呼称します
• 英語だとClassical Computerですので、従来型のくらいのイメージでしょうか

なので、古いとか、ましては、遅いとかっていう意味ではありません。
では、普通のコンピュータの特徴とは何でしょうか？議論は、色々ありそうですが、

• 古典ビット ：計算で利用するビットは、「0か1」のどちらか
• 逐次計算 ：複数の入力を与えても、１個づつ³処理をして計算（入力の数だけ計算）

といった点ではないでしょうか？では、量子コンピュータになるとどうでしょうか？

量子コンピュータ

古典コンピュータの逐次計算が苦手とする、複数の状態を同時に扱うような問題に対し、
量子力学での「重ね合わせ・もつれ合い」という現象がうまく生きるようにプログラムを構成し、並列・一括での計算を実現しよう。というのが量子コンピュータです。

量子コンピュータでは、上記の２要素が下記となります。

• 量子ビット ：計算で利用するビットは、 「0と1の重ね合わせ」 を取れる。
• 並列計算 ：それにより、複数状態を同時に表現し、それらを 並列に(一括で) 計算できる

「重ね合わせ」 とか 「一括で」 とか、早速、よう分からんですね。。
イメージしろと言われても、無理な話ですね。

前提として

「重ね合わせ・もつれ合い」等の量子力学的な現象ですが、理解するのがどれだけ困難か？
ですが、かの有名なリチャード・P・ファインマン⁴先生のお言葉を借りると

If you think you understand quantum mechanics, you don't understand quantum mechanics.⁵
もしも量子力学を理解できたと思ったならば...それは量子力学を理解できていない証拠だ。⁶

つまり、研究者ではない一般人が理解を試みる事、そのものが、おこがましいのですが、、
一方で、現象の本質は理解できずとも、その活用が計算を高速化する可能性があるなら、
それは、計算機科学の立場の人間からすると、とても魅力的に思えます。

というわけで、今日お話したいこと

量子コンピュータの本質に迫る！みたいな記事は私には書けませんが（笑）、、

• 「重ね合わせ」 がどんなイメージか？
• なぜ、それにより 並列計算が実現されるか？

について 数式は使わずに、イメージで お伝えしてみたいと思います。
量子力学の本質は分からない、が、計算高速化に可能性を感じる一般的なエンジニアとして。。

今までの議論と説明のアウトライン

古典コンピュータと量子コンピュータを、ビットと計算方式で比較しました。
整理すると、

	ビット	計算方式
古典 コンピュータ	古典ビット (0と1)	逐次計算
量子 コンピュータ	量子ビット (0と1と①重ね合わせ)	②並列計算

といった状況ですので、「①重ね合わせ」のイメージをご説明し、
それが「②並列計算」にどうつながるか？の順序で説明を進めます。

①重ね合わせ

コイン　と　コイントスで考える⁷

急になぜコインが出てくるか？というと、みなさんが良くご存知のコイントスにて、重ね合わせをうまく説明できそうだからです。では、話を進めましょう。

コインで数字を表現する

たとえば、手元にコインが１枚あったとしたら、表(0)と裏(1)を使うと、0と1が表現できます。

複数枚あると、２進数でいろいろな数字を表現できる

たとえば、３枚のコインがあれば、「0～7の数字を同時に一つ表現することができます。」
「同時に一つ」 というのがとても重要です。どういう意味かというと、

• 5を表現することもできるし、7を表現することもできる。
• 一方、5と7を同時には表現できず、5→7に変更しようとすると2枚目を裏返す必要がある
• 0と1を同時に両立するコイン!? があれば、2枚目をそれにすれば、5と7を同時に表現できるのですが…

表(0)でも裏(1)でもない、コインを考える

ここで、表／裏向きのコインについて、見方を変えてみると、、
「100%で表(0)の状態」、「100%で裏(1)の状態」 と考えることができそうです。

これらと対比して、 コイントスし、くるくる回るコイン を考えると、この くるくるコイン は、「表(0)になるかもしれないし、裏(1)になるかもしれない」 と言った様に、
両者の確率を50%／50%で両立する状態。つまり両者が、 「重なり合った状態」 と
見ることができるのでは無いでしょうか？

くるくるコイン　と　重ね合わせ

「重ね合わせ」を「くるくるコイン」として模すことができたので、、
改めて、古典／量子ビットの違いを見てみましよう。

• 古典ビット　：　0か1　を決定的（100%）に表現する。
• 量子ビット　：　0か1　を確率的（例50% vs 50%）に⁸表現し、重なった状態も取れる

「ファインマン先生、重ね合わせが、よく分わからないのです!!」

ここまで、説明すると、、

• 「ゼロ　と　イチ」が重なっているけど、データ混じらないの?
• そんなものに、どうやってアクセスすればいいの
• 「計算」なのに、あとは、「偶然に任せる」 的な理屈でいいの

とか、色々不安がでてくるのですが、ここで、ファインマン先生の言葉を思い出してください。

If you think you understand quantum mechanics, you don't understand quantum mechanics.⁵
もしも量子力学を理解できたと思ったならば...それは量子力学を理解できていない証拠だ。⁶

現象そのものを理解しきるのは困難です。（それは、専門家でも理解の厳しい世界ですので。。）
一方で、これを受け入れる（前提とする）とどんな世界が見えてくるでしょうか？
この 「くるくるコイン」を受け入れたとしたら 、どんな計算ができるか？を見ていきましょう

②並列計算　～重ね合わせを受け入れると見える世界～

並列に計算するためには？

どうすればいいでしょうか？まずは、計算対象を並列に（同時に）表現する必要があります。
並列に（同時に）表現というのは、ちょっと乱暴な言い方でしたね。
では、旅行のプランを例に考えてみましょう。検討している旅行プランが３パターンあり、

• パターンA　：　その国の世界遺産をすべて回る、費用も高い、疲れるが大満足
• パターンB　：　１つだけ世界遺産に行き、浮いたコストで、美味しいレストランへ
• パターンC　：　１つだけ世界遺産に行き、浮いたコストで、最終日のホテルをランクアップ

満足度が高く、コストもそこそこ、体力面も考慮し、一番ベストなプランを選びたい。
逐次計算では、計算機に同時に入力できるのは、任意の１パターンです。

一方で、計算対象を 並列に（同時） に表現でき、それを処理できる並列計算機があれば、
こんなふうに、全部のパターンを同時に表現し、計算を行うことができます。入力は１回だが、全部のパターンを同時に（確率的に1/3で両立する）表現なので並列計算ができるイメージです。⁹

並列に計算対象を表現するのに、便利なものはなかったか？

並列に、同時に、複数のパターンや状態を表現するのに、便利なものはなかったか？
そうです、先程、 強引に受け入れて頂いた「重ね合わせ」 です。
旅行を例に出しましたが、もうすこし簡単な議論にしたいので、コインの世界に戻りましょう。
ただ、コインを複雑化していけば、旅行の最適化だってできるはずです。

0～7を同時に表現したい。

では、0～7という状態を同時に表現する方法を考えていきましょう。

まずは、古典ビット（24枚必要。。）

0（000）～7（111）を同時に表現しようとすると、

• １パターンあたり、コイン（ビット）が３つ必要です。
• その上で、0～7の8パターンを表現するためには、3x8=24枚のコイン（ビット）が必要です。

なにが言いたいかというと

• １つのパターンが、ちょっとでも複雑になったり（3枚→30枚）
• 表現したいパターン数が、ちょっとでも増えると（8パターン→80パターン）

すぐに、組み合わせ爆発を起こしそう。ということです。

つぎに、量子ビット（なんと、、◯枚）

ここで、「重ね合わせ」が力を発揮します。
1桁目、2桁目、3桁目と3つのコインを重ね合わせにします。
そうすると、全部のコインが、 0 : 1 = 50% : 50% の重ね合わせだとすると、全体としては、
0～7の8パターンが、それぞれ、出現確率1/8 で重なりあっている状態と理解できます。

そして、古典の24枚と比較すると、必要なコインの枚数は3枚です！なんと3枚です！
具体的には、コインN枚に対して、表現可能な状態は、$2^N$パターン¹⁰となります。

そして、コインの枚数が50枚になる頃には

$2^{50}$パターン（bit）となるので、

• 原理上、規模的にはペタバイト級の空間を手に入れることができます。¹¹
• もっとすごいことを言うと、50→51になるだけで、$2^N$ですから空間は２倍になります。
• もう、すごいんです。バイバインです。栗まんじゅうも食べたい放題です。

まとめ

改めて冒頭にお示しした、この表を眺めておしまいとしたいと思います。

• 古典／量子コンピュータの違いを、「ビット」と「計算方式」の２面で眺めてみました
• 量子ビットは「重ね合わせ」を取ることができます。
• それにより、様々なパターンを同時に表現し、並列計算が実現可能です（原理上は）

	ビット	計算方式
古典 コンピュータ	古典ビット (0と1)	逐次計算
量子 コンピュータ	量子ビット (0と1と①重ね合わせ)	②並列計算

原理上は

最後に、一言 「原理上は」 とか、気になる表現をしてしまいスミマセン。
ただ、これを説明するためには、もっと各論が必要になってきます。
ただ、この原理上はという現実も、皆様には是非ご理解頂きたいポイントになります。
そこで、本アドベントカレンダーでは、「理想的には～」と「現実的には～」の両方のテーマをあわせてご紹介・ご説明していければと考えています。

明日以降もよろしくおねがいします～

おまけ

重ね合わせは、空想科学（SF)とかではないのです。

空想的な話・仮想的な話　と誤解されがちですが、現実です。
詳細を知りたい方は、こちらを参照されていただければと（リンクさせていただきます。）

1. 手前味噌で恐縮ですが、所属組織のHPの解説より引用しております。詳細については、下記をご確認ください。https://www.nri.com/jp/knowledge/glossary/lst/ra/quantum_computer ↩

2. https://ja.wikipedia.org/wiki/%E5%8F%A4%E5%85%B8%E5%8A%9B%E5%AD%A6 ↩

3. マルチスレッドとかマルチプロセスプログラミングも、マシン語レベルでは、CPU時間を時分割し多重化しているので、ある瞬間（単位時間）でみれば１つというのは正しいかと ↩

4. https://ja.wikipedia.org/wiki/%E3%83%AA%E3%83%81%E3%83%A3%E3%83%BC%E3%83%89%E3%83%BBP%E3%83%BB%E3%83%95%E3%82%A1%E3%82%A4%E3%83%B3%E3%83%9E%E3%83%B3 ↩

5. https://en.wikiquote.org/wiki/Talk:Richard_Feynman#%22If_you_think_you_understand_quantum_mechanics,_you_don't_understand_quantum_mechanics.%22 ↩ ↩²

6. 意訳してみました。直訳だとなんだかむ無味閑散な感じでしたので。 ↩ ↩²

7. Aleksandar Radovanovic, Quantum Programming Illustratedを参考にさせていただきました ↩

8. 実際には、複素確率振幅という複素数の絶対値（２乗）が、そのパターンを観測する確率となるのですが、まずは、ざっくり確率として捉えて頂ければと。悲しきかな、人類はその複素確率振幅に直接的にアクセスすることはできず、複数回観測による頻度確率から類推するしかないわけですが。。 ↩

9. Groverのアルゴリズムをイメージして記述してみました。このアルゴリズムは、カレンダの後半で扱っていきますので、ご興味有る方は、カレンダの後半で。 ↩

10. 数式使わない宣言でしたが、使っちゃいましてTex数式。スミマセン。 ↩

11. 実際には、量子系のノイズに対応し、誤り訂正をする関係でもっと空間が小さくなる。（詳細は、量子誤り訂正の回でやります。）空間が広大過ぎても、正解に対応するパターンの複素確率振幅が小さくなり、制御精度を要する。頻度確率で正解を見つける関係で、必要な観測回数が増えるので測定回数が多くなる等、課題はいろいろあります。 ↩