はじめに
下記のとおり、qutipを用いるとブロッホ球を描画することができます。
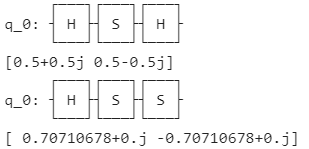
Qiskitやblueqatにて量子計算のシミュレーションをすると、下記の様な状態ベクトルを得ますが、
このままでは、qutipに入力することが出来ず、少し加工が必要なので、
その加工をメモっておきたいと思います。(作業メモです)
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
加工方法
冒頭に掲載した、状態ベクトルですが1量子系では、$\ket{0}$と$\ket{1}$の確率振幅(係数)です。
qutipでは、$\ket{0}$や$\ket{1}$を、basisという関数で表現するので、下記の様な可能が必要となります。
from qutip import *
state_vector = [0.5+0.5j,0.5-0.5j]
qutip_object = state_vector[0] * basis(2,0) + state_vector[1] * basis(2,1)
では、basis(N,n)とは何でしょうか?
に記載のとおり、大きさNのヒルベルト空間において、状態nを表現するのがbasisです。
つまり、
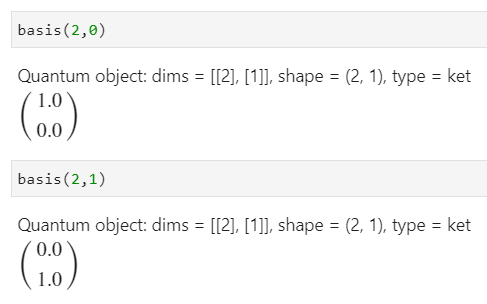
basis(2,0)
basis(2,1)
はそれぞれ、$\ket{0},\ket{1}$を指します。
よって、冒頭のソースの様に、$\ket{0},\ket{1}$に対応する確率振幅(複素数)をかけ合わせ足し込めば、Qutipで利用できるオブジェクトに変換を行うことが出来ます。

このオブジェクトを、add_statesメソッドにわたすことで、ブロッホ球を書くことも可能です。

おまけ
ユニタリーゲートで計算しているうちは、状態ベクトル$\ket{\psi}$の確率振幅$\alpha,\beta$は規格化条件を満たしていると思うので不要な操作ではあるのですが、規格化条件を満たさない場合には、**unit()**をコールすることでユニタリーにすることができます
\displaylines{
\ket{\psi} = \alpha\ket{0} + \beta\ket{1}
\ \ \ \ \ (\alpha,\beta \in \mathbb{C})
\\
|\alpha|^2 + |\beta|^2 = 1
\ \ \ \ \ (規格化条件)
}
例えば、下記の様に、$\ket{\psi_1}$は規格化条件を満たしますが、$\ket{\psi_2}$は満たしません
\displaylines{
\ket{\psi_1} = \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1}
\ \
\leftrightarrow
\ \
|\alpha|^2 + |\beta|^2 = 1
\\
\ket{\psi_2} = 1\ket{0} + 1\ket{1}
\ \
\leftrightarrow
\ \
|\alpha|^2 + |\beta|^2 = \color{red}{2}
}
こういったときは、qutipのunit()をコールすると強制的にユニタリーにすることができます。
普通は使いませんが、三角関数等で座標計算する際に計算誤差が気になるときは、このunit()をコールしておくのが良いかもしれません。
まとめ
簡単な作業メモですが、qutipで状態ベクトルをそのまま渡す方法がなかったため作業メモとして起こしました。
なお、qutipでブロッホ球を描いた際に、ブロッホ球が歪むことがあるので、その際は下記参照ください。