この記事について
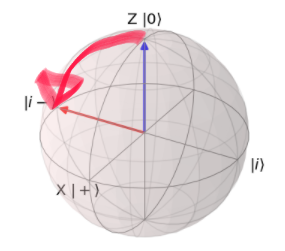
$|0\rangle$から、$|i-\rangle$への回転に関して、
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
HSH\ket{0} \equiv\ket{i-}
\ \ \ \ \ \ \ \
Rx(\pi/2)\ket{0} \equiv\ket{i-}
どちらも、$\ket{i-}$となり計算結果が一致しそうですが、結果が一致しません。
果たして、何故でしょう。という、小ネタ(作業メモ)です。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
結論から
$Rx(\pi/2)$と$HSH$は、グローバル位相が異なります。なので計算結果がズレる。
確率振幅や相対位相は一致しているので、観測すると結果は同一となります。
ただし、シミュレータ等で計算過程の状態ベクトル等を取り出すと、
グローバル位相分ずれた結果となります。
問題の確認
Rx(π/2)|0>
X軸を中心に$\pi/2$回転なので、$Rx(\pi/2)\ket{0} \equiv\ket{i-}$となりそうです。
HSH|0>
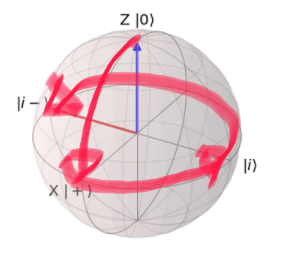
最初の$H$で$\ket{+}$へ、$S$で$\ket{i}$へ、そして、$H$で$\ket{i-}$に到達します。
なお、HSHの回転の詳細は、下記をご確認ください。
計算結果
両者の計算結果を下記に整理します。なおQiskitでの計算のソースは、後述します。
| $Rx(\pi/2)$の計算結果 | $HSH$の計算結果 | |
|---|---|---|
| 回路 | 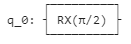 |
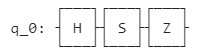 |
| ブロッホ球 | 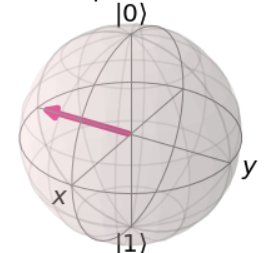 |
 |
| 結果 | [0.70710678+0.j 0. -0.70710678j] | [0.5+0.5j 0.5-0.5j] |
| 数式にすると | $\ket{0}+i\ket{1}/\sqrt{2}$ | $\frac{1+i}{2}\ket{0}+\frac{1-i}{2}\ket{1}$ |
グローバル位相をくくりだす
この2つの実行結果ですがグローバル位相をくくりだすと、両者とも$\ket{i-}$となります。
Rx(\pi/2)\ket{0} = \frac{1}{\sqrt{2}}(\ket{0} - i\ket{1}) = \ket{i-}
一方で、
HSH\ket{0} = \frac{(1+i)}{2}\ket{0} + \frac{(1-i)}{2}\ket{1}
ですが、後者は、
\displaylines{
\frac{(1+i)}{2}\ket{0} + \frac{(1-i)}{2}\ket{1}
=\frac{(1+i)}{2}\ket{0} -i \frac{(1+i)}{2}\ket{1}
\\
=\frac{(1+i)}{\sqrt{2}} \times \color{red}{\frac{\ket{0}-i\ket{1}}{\sqrt{2}}}
\\
=\frac{(1+i)}{\sqrt{2}}\color{red}{\ket{i-}}
}
と式変形できるので、
- グローバル位相を無視すると、結果が一致する。一方で、
- シミュレータで状態ベクトルを取得すると、グローバル位相も含まれた値が得られる
- ブロッホ球上では、グローバル位相は無視されるので、結果が一致しているように見える
という落ちでございました。
(おまけ)ソース
Qiskitで計算してみたソースを掲載しておきます。(簡素なもので恐縮です)
Rx(π/2)|0>
from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
from qiskit.visualization import plot_bloch_multivector
import math
# Rx(π/2)|0>
qc = QuantumCircuit(1)
qc.rx(math.pi/2,0)
print(qc)
state = Statevector.from_instruction(qc)
print(state.data)
plot_bloch_multivector(state,title="")
HSH|0>
# HSH|0>
qc = QuantumCircuit(1)
qc.h(0)
qc.s(0)
qc.h(0)
print(qc)
state = Statevector.from_instruction(qc)
print(state.data)
plot_bloch_multivector(state,title="")