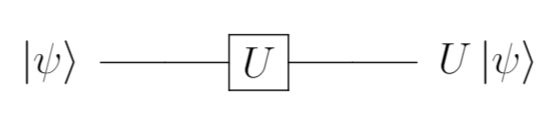この記事について
量子 テレポーテーションでは、量子状態を遠隔地に転送しました。
では、量子ゲート テレポーテーションでは、何を転送するでしょうか。
そうです。量子ゲート(の作用)です。
分かるようで分からない、ゲートテレポーテーションについて見ていきたいと思います。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
$$
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \ #3 & #4 \end{bmatrix}}
$$
量子ゲートを転送するとは?
量子ビットにユニタリゲートを適用したい
突然ですが、状態が$\ket{\psi}$である量子ビットに、任意のユニタリゲート$U$を適用したい時どうするでしょうか。
きっと、その量子ビットに対して、ユニタリーゲート$U$を適用し下記の様な回路を組むのでは無いでしょうか。
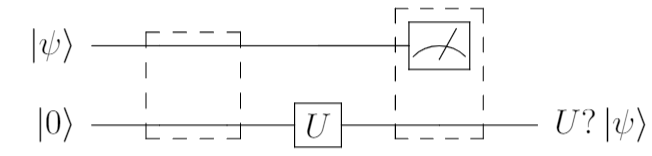
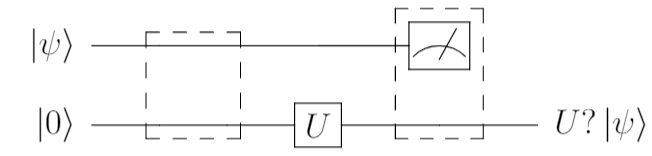
ちょっと意地悪な状況
では、ちょっと意地悪な状況を考えます。
- 上述のように、状態$\ket{\psi}$に対して、ユニタリーゲート$U$を適用し、$U\ket{\psi}$を作ってください。
- ただし、その量子状態を持つ量子ビットに対して直接ゲートを適用してはいけません。
つまり、
といった状況ですが、こんな魔法の様なことは、さすがにてきません。
そこで、補助量子ビットを1ビット追加して、上記を達成出来ないかを考えてみます。
補助量子ビットを追加する
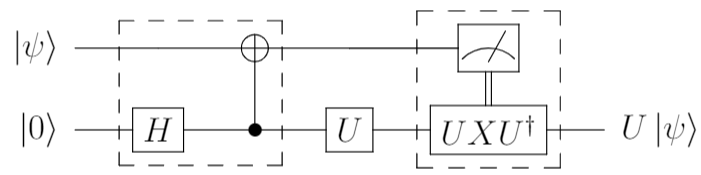
補助量子ビットを1本追加しました。(下の線)この状況で、
- 補助量子ビット側に、ユニタリゲート$U$を適用するのだが、そのゲート適用の作用や効果を
- $\ket{\psi}$のビットに転送し、この2ビットにより、$U\ket{\psi}$の状態を作り出す
- そのために、破線の周辺に対して、少し操作を行う。
こんなことができるのでしょうか?
答えはYes。で、できるんです。これが、ゲートテレポーテーションです。
なぜ、こんな周りくどいことをするのかというと、量子誤り訂正符号にて間接的にゲート適用を行いたいシーンがあります。
ただ、それは本記事の説明の範囲を超えるので、最後に少しだけ触れる程度としたいと思います。
ゲートの作用を転送する
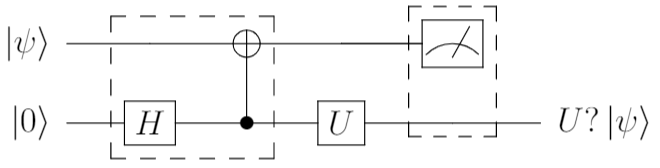
左の破線の中を埋めてみる
左側の破線の中ですが、どういった回路を構成すれば良いでしょうか?
実を言うと、Bell回路を構成することで、$\ket{\psi}$に対して、間接的にゲート$U$を適用することができます。
計算で確認
実際に、$U\ket{\psi}$を上記回路でつくりさせるか?を確認しておきましょう。
$$
\ket{\psi} = a\ket{0} + b\ket{1}
$$
としたときに、$H\ket{0} = \ket{+}$の状態を数式で表現すると
\displaylines{
\ket{\psi}\kets{+} = (a\ket{0} + b\ket{1}) \otimes \frac{1}{\sqrt{2}} \left( \ket{0} + \ket{1} \right)
\\
= \frac{1}{\sqrt{2}} \left( a\ket{00} + a\ket{01} + b\ket{10} + b\ket{11} \right)
}
これに、$Cnot_{21}$を適用するので
\displaylines{
Cnot_{21}\ket{\psi}\kets{+}
= \frac{1}{\sqrt{2}} \left( a\ket{00} + a\ket{11} + b\ket{10} + b\ket{01} \right)
\\
= \frac{1}{\sqrt{2}} \left( \ket{0} \otimes ( a\ket{0} + b\ket{1}) + \ket{1} \otimes ( a\ket{1} + b\ket{0}) \right)
\\
= \frac{1}{\sqrt{2}} \left( \ket{0} \otimes \ket{\psi} + \ket{1} \otimes X\ket{\psi} \right)
}
この状態にて、補助ビットである2ビット目にユニタリゲート$U$を適用します。
U_{2}Cnot_{21}\ket{\psi}\kets{+}
= \frac{1}{\sqrt{2}} \left( \ket{0} \otimes U\ket{\psi} + \ket{1} \otimes UX\ket{\psi} \right)
上記のユニタリーゲートがかかった項に着目すると、たしかに、$U\ket{\psi}$の状態ができています。
U_{2}Cnot_{21}\ket{\psi}\kets{+}
= \frac{1}{\sqrt{2}} \left( \ket{0} \otimes \color{red}{U\ket{\psi}} + \ket{1} \otimes \color{red}{UX\ket{\psi}} \right)
ここまでの結果を整理
この回路に従い、計算を進めた結果を整理しておきます。
上記は、元々、$\ket{\psi}$の状態であったメインのビットの観測結果に従い、補助ビット側に異なる状態を出力します。
具体的には、下記の様な関係です。
| # | 1ビット目の観測結果 | そのときの、2ビット目がとる状態 |
|---|---|---|
| 1 | $0$を観測 | $U\ket{\psi}$ |
| 2 | $1$を観測 | $UX\ket{\psi}$ |
上記を見ると、所望の状態の$U\ket{\psi}$に対して、
1ビット目で、$1$を観測したときには、余計な$Not(X)$がついてしまっています。
右の破線の中を埋めてみる
この余計な、$Not(X)$をキャンセルするためにはどうすれば良いでしょうか?
そうです。右の破線の中に、
1ビット目で$1$を観測したときに2ビット目に作用する、$Controlled \ Unitary$を考えましょう。
$UX\ket{\psi}$ を所望の状態である $U\ket{\psi}$にするには、下記のようなゲートを適用してはいかがでしょう?
UXU^\dagger
計算で確認してみると
U^\dagger U = XX = I より
\ \ \
UXU^\dagger \ UX\ket{\psi} = \color{red}{U\ket{\psi}}
つまり、右の枠にはこんな$Controlled \ Unitary$を入れておけば、つじつま合わせができるでしょう。
一般化しておく
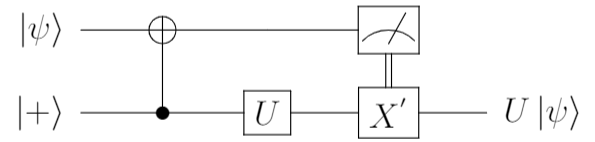
上記では、少し込み入った感じがするので、整理し一般化しておきましょう。修正点は下記2点です。
- $H\ket{0} = \kets{+}$を補助ビットの初期状態とする
- 辻褄合わせのゲートを$X' = UXU^\dagger$とおいておく
上記で整理するとこんな回路になります。
これで、ゲートテレポーテーションの完成です。
$\ket{\psi}$の量子ビットに直接触れることなく、ユニタリーゲート$U$を適用することができました。
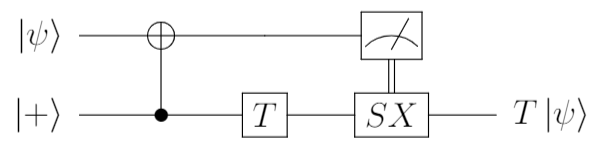
U = ゲートT のテレポーテーション
最後に、量子誤り訂正符号の論理量子ビットの操作にて、論理$T$ゲートを適用するために、ゲート$T$のテレポーテーションを確認しておきたいと思います。なぜ、ゲート$T$なのかというと、$T$は、ユニバーサルゲートセットの構成要素の為、ゲート$T$が使えると、何かと便利な状況がある。だから、ゲート$T$のテレポーテーションを確認しておく。と理解頂ければと思います。1
上記で、一般化した回路に$U=T$を代入すると下記となります。
なぜ、$X'=SX$となるかは、計算で確認しておきましょう。
適用するゲート$U$に対して、$X'=UXU^\dagger$なので、$U=T$では、$X'=UXU^\dagger=TXT^\dagger$
これを計算すると、
TXT^\dagger = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4} \end{bmatrix}\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4} \end{bmatrix} = e^{-i\pi/4}\begin{bmatrix} 0 & 1 \\ i & 0 \end{bmatrix}
と、グローバル位相以外は$SX$と等しくなります。
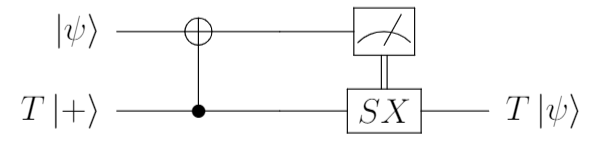
そのうえで、$T$の適用タイミングですが、$Cnot$ゲートの前に持ってきて下記のようにしても計算結果が一致します。
これで、補助ビットとして$T\ket{+}$を準備することで、任意の1量子状態$\ket{\psi}$に対して、直接的にゲートを作用させる事なく、ゲート$T$を作用させることができる。ゲートの作用を転送できること が確認できました。
まとめ
量子ゲートのテレポーテーションである、ゲートテレポーテーションについて扱いました。
仕掛けとしては理解できたのですが、上述の量子誤り訂正符号のシーン以外でも何らか活用の機会があるのでは?
と思うものの、こういうときにゲートテレポーテーションって便利だよね。
という応用例はまだ理解できていないので、お詳しい方いらっしゃればコメント等頂ければと思います。
なお、よろしければLTGM頂ければ嬉しいです。
参考
-
${CNOT,H,T}$でユニバーサルゲートセットが構成できるのでTゲートについて触れています。ゲートテレポーテーションにおいて$T$を扱っている理由としては、計算中に発生する誤り対応すべくスタビライザー符号等の誤り耐性符号上での演算を想定するのですが、スタビライザー符号上での演算は、スタビライザーを破壊しないようにクリフォード演算に閉じる必要があります。一方で、${CNOT,H,T}$のうち、$T$はクリフォード演算では無いため、$T$を符号上の演算で利用しようとすると、$T$の効果を事前に準備して、適用するような操作が必要となります。この背景で、$T$のゲートテレポーテーションを扱っています。 ↩