昔々、膝に矢を受けてニートをしていた後に諸々のコーディング実力判定サイトから求職活動をしてみたことがありました。その際、これ(アルゴリズムの)コーディング実力判定サイトじゃね・・・?ということに気付き、箔をつけるために独学で探索アルゴリズムを勉強した時のことをまとめました。独学で頑張った結果、珍奇な理解になっているのではないかと疑われます。
想定する読者層の方
- 実務的なプログラムは書けるが、アルゴリズムを触ったことがない。
- コーディング実力判定サイトで実力試しに問題を解こうとしたら、これ(アルゴリズムの)コーディング実力判定サイトじゃね・・・? と思った。
- 探索に関して変な理解が身についても怒らない。
上記に当てはまらない方、真面目でまっとうな記事を読みたい方はそっと×ボタンを押したほうがよいと思います。すみません。万が一経験者の方のアドバイスないしご指摘などいただけることがあったら謹んで受け取りたいと思います。
探索とは
参考動画リンク
動画内1:30頃のムーブをコンピュータにしてもらう、というイメージです。一言で言うとマシンパワーで実際に総当たりして答えを見つける方法という認識です。とりあえずこの実装ができるようになっただけでアルゴリズム実力判定サイトの問題で解ける問題が一気に増えました。実装方法を知らないと全く戦えないという点でアルゴリズム界における某漫画の念能力に等しいと言えます(探索以外で解く問題も多々ある中、あえて断定することで炎上を狙う高等テクニック)。
探索するための準備
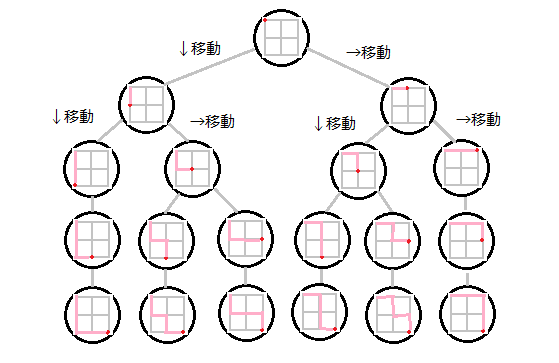
問題文から、図の様な状態遷移?のイメージをもてるときは探索が使えるという感想です(後述の例題を図にしました)。
問題の中で下記二つを考えます。
- 状態を表すのに必要な変数
- 分岐を一つ進んだ状態にするのにどのように変数操作をすればよいか
後はその状態を表す変数に関しまして
- 変数を引数とし、操作をする再帰関数(末端判定入り)にわたす→深さ優先探索になる
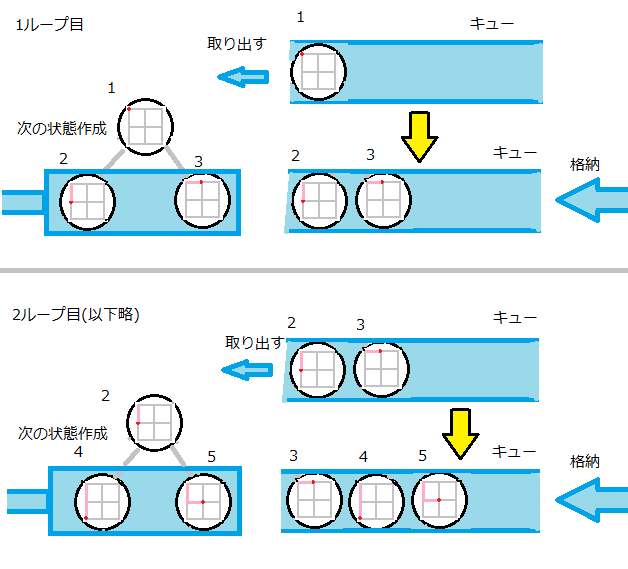
- 変数を保持するオブジェクトを作ってキューに格納、実行部分で一つ取り出して実行して次の分岐の状態データをキューに格納することをキューからデータがなくなるまで繰り返す→幅優先探索になる
という認識です(他の実装方法もあるようですが筆者が習得しておりません)。
たぶん下記の例題をもとに具体的に見て考えた方がイメージがつくかと思います。
深さ優先探索とは
とりあえず最初(root)から末端まで進めるまで進んで
進めるところがなくなったら一つ前に戻ってまだ進んでいない分岐を進む
進んでいない分岐がなかったらもう一つ前に戻ってまだ進んでいない分岐を進む
以下繰り返し
具体的な実装方法として、先述の通り、終了条件を含む再帰関数を使うのがメジャーという認識です(関数の積み重ねがそのまま図の構造のようになるイメージ)。全部探索する場合、例えば通り数なら条件を満たした時にカウントアップのような処理を入れることで求める通り数を得ることができます。
例題
2x2のマス目がある。左上から右下までの最短経路の通り数を深さ優先探索で求めよう。
感想
最短という縛りがあるため右と下への移動分岐だけ考えればよく、また必ず右下にたどり着くので終了条件は「右下に来た時((2,2)の時」にできます。今回の場合
・今の状態を表すのに必要な変数・・・座標(x,y)
・一歩進んだ状態・・・y座標に+1(下に移動)x座標に+1(右に移動)の二つ
端だとそれ以上進めなくなる方向があることに注意して実装したいと思います。
なおこの問題に限らないのですが、探索で求めなくても別に数学的に解ける問題もあります(むしろ数学的に解ける場合はほとんどそちらを選択した方が早い印象です)。探索が一番楽な解法になり、かつ簡潔な問題を知らないので許してください。
コード
java(1.7)での実装です。他の言語の方は適宜自分の言語に落とし込んでみてくださったらありがたいです。
public class DfsPractice {
//finalがつくと定数
private static final int SIZE = 2;// マスの数
//(クラス変数;とりあえず下のメソッド(dfs)の内部から自由に読み書きできます)。
private static int count = 0;// 通り数
//実行部分(javaはmainから実行される)
public static void main(String args[]) {
dfs(0, 0);
System.out.println(String.format("全部で%d通り", count));
}
/**
* 深さ優先探索用再帰関数 SIZEが2の時下記のイメージ
* 012(x方向)
* 0┌┬┐
* 1├┼┤
* 2└┴┘
* (y方向)
* @param int x x方向の位置(左を0とする)
* @param int y y方向の位置(上を0とする)
*/
private static void dfs(int x, int y) {
// 終了(末端)判定を最初に書くことが多い。
if (x == SIZE && y == SIZE) {
count++;
return;
}
//ここからは分岐 こちらで分岐する条件に合わなくなった結果、分岐なしで戻る書き方にする場合もある。
//下方向への分岐
if (y < SIZE) {
dfs(x, y + 1);
}
//右方向への分岐
if (x < SIZE) {
dfs(x + 1, y);
}
}
}
初期はどのように関数が呼ばれるか個人的に分かりづらかった記憶があるため、多少情報を増やしたバージョンも置かせていただきます。実際の表示は長くなるので省略しますが、ひまなら動かしてみて、ログを図と合わせて追ってみると理解が進む気がしました。
public class DfsPractice {
private static final int SIZE = 2;//盤面のサイズ
private static int count = 0;//通り数
public static void main(String args[] ) {
dfs(0, 0, 0);
System.out.println(String.format("全部で%d通り", count));
}
/**
* 深さ優先探索用再帰関数
* SIZEが2の時下記のイメージ
* 012(x方向)
* 0┌┬┐
* 1├┼┤
* 2└┴┘
* (y方向)
* @param int x x方向の位置(左を0とする)
* @param int y y方向の位置(上を0とする)
* @param int hosuu 今何歩目か(depth)
*/
private static void dfs(int x, int y, int hosuu){
//終了判定を最初に書くことが多い。
System.out.println(String.format("現在の状態(%d, %d) %d歩目", x, y, hosuu));
if(x == SIZE && y == SIZE){
//今回は右下に来たことが分かったらその通り数をカウントして終了させるとよい。
count++;
System.out.println(String.format("末端に到着(%d通り目)。一つ前の状態に戻る", count));
return;
}
//まだ終了していない場合、状態を変化させて分岐をする。
if(y < SIZE){
System.out.println("下へ移動する分岐へ(y+1)");
dfs(x, y+1, hosuu+1);
System.out.println(String.format("戻ってきた:状態(%d, %d) %d歩目", x, y, hosuu));
}else{
System.out.println("これより下へ進めないため下方向への分岐は行わない");
}
if(x < SIZE) {
System.out.println("右へ移動する分岐へ(x+1)");
dfs(x+1, y, hosuu+1);
System.out.println(String.format("戻ってきた:状態(%d, %d) %d歩目", x, y, hosuu));
}else{
System.out.println("これ以上右へ進めないため右方向への分岐は行わない");
}
if(hosuu > 0){
System.out.println("一つ前の状態に戻る");
}else{
System.out.println("一つ前の状態に戻る(探索の終了)");
}
}
}
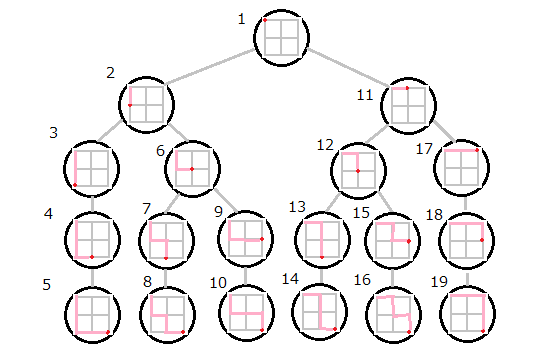
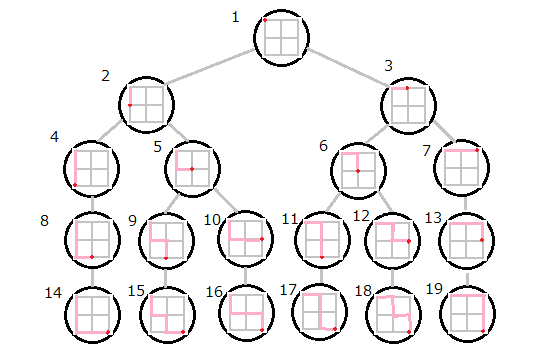
(参考)幅優先探索とは
図の順番のように最初(root)に近い部分から確認していく探索方法です。
先述の通りですが、変数を保持するオブジェクトを作ってキューに格納、実行部分で一つ取り出して実行して次の分岐の状態データをキューに格納することをキューからデータがなくなるまで繰り返す処理で実装できます。
答えが見つかった時に最短距離になる性質があるようです。そのため、迷路の最短経路を一つ求めればよい問題の場合などで使うと、見つかった時点で打ち切れば答えをとれるため深さ優先探索より楽でした。有限の状態を全部探索する場合は深さでも幅でもさほど変わらないように思います。
独学方法を考える
アルゴリズムは数学が得意な人が強いらしいので
数学の勉強方法に倣うことが最適なのではと考えました。
・深さ優先探索の実装例を見る
・基本問題を解く(深さ優先探索をただ実装すれば解ける問題を解く)
→解けなかったら解答を見て、もう一度解いてみる
・応用問題を解く(深さ優先探索をただ実装するだけでは解けず、一工夫必要な問題を解く)
→解けなかったら解答を見て、もう一度解いてみる
しかし数学に例えたことで私の中で拒否反応が起こってしまいました。
応用問題の傾向を考える
難易度の高い問題は何のために一工夫が必要になるかを考えてみました。
素直に実装すると非常に実行時間がかかる
参考動画リンク
ただ、googleで「爆発 お姉さんを救う方法」あたりで検索して解法を調べると分かるのですが、この問題は非常に難しい問題のようです。答えの通り数を見て私の様な者ですら難しさを感じ取とれました。俺にお姉さんは救えねえんだよ・・・!
上記のような超高難度の問題にいきなり挑戦すると挫折すると思われます。自分の場合はコーディング実力判定サイトの難易度低めの問題から考えたり、実際送って時間切れエラーになってから枝刈など考えたりしました。解答例が公開されるイベント問題のようなものでは、解答例から時間短縮のテクニックを学んだりする形で少しづつ頑張ったりしました。
(注)枝刈とは探索の際、明らかに求める答えに到達しない事が分かった分岐は探索を行わないことで、時間を短縮する手法のこと。
素直に実装すると無限ループする
お姉さん的な問題でも何も考えず上下左右にただ分岐するだけで実装すると下→上→下→上・・・で無限ループできます(しかも同じ道を通る不適ムーブになるおまけつき)。それ以外でも操作の結果、過去に通った状態と同じ内容になる場合、深さ優先探索では無限ループしてしまって解が求められない問題があるようです。今まで通った経路の情報を保存して、通ったことのある状態には進まないようにするアプローチなどが有効な場合があります。答えを一つ見つければよい場合などは、幅優先探索の方が有効な場合もありました。
素直に実装するとメモリが足りない
上記の枝刈や無限ループ防止のために、状態を普通にメモリ保存しようとすると足りなくなる場合難易度が上がります。自分が解けたことのあるもので最多状態と思われる問題だと、状態の無限ループが起こりうるパズルの解法(状態が約21テラ通り)を求める探索などがありました(ただ、その問題自体はほぼ素直な幅優先探索で解けました)。
動的計画法(メモ化再帰)
最後に深さ優先探索の時間短縮のテクニックの一つである動的計画法(メモ化再帰)の個人的理解をまとめて終わりたいと思います。
動的計画法(メモ化再帰)とは
キャッシュです(断定することによる炎上テクニック)。
キャッシュとは
結果を求めるのに時間がかかる処理で、与えたパラメータ(ページのurlであったり関数の引数であったり)が同じ時に戻ってくる処理結果(htmlであったり戻り値であったり)が変わらない場合、パラメータと、その処理結果を保存しておいて二回目からはそれを使うと爆速になる仕組みのことと勝手に定義させていただきます。
処理に時間がかかる理由はネットワーク通信だからであったり
DBのIOなどを含んでいるからであったりフィボナッチ数列の再帰関数だからであったり様々です。
例「ブラウザのキャッシュをクリア」のキャッシュ
ネットワーク越しにいちいちデータを取得しに行くより、
そのページの内容を最初に取った時にブラウザがページのurlに対応するデータを保存しておき、同じurlの場合保存していたデータを表示すると爆速である。キャッシュをクリアするともう一度取りに行く必要が出るので次の一回が遅くなる。ページに更新があった場合はキャッシュをクリアしないと更新が反映されないのでたまに頭を悩ませる原因になる。
例題 フィボナッチ数列
f(0)=0,f(1)=1,f(n+2)=f(n+1)+f(n) (n≧0)
上記の条件でnが50の時の値をもとめてください。なお再帰関数として実装することとする。
筆者の感想
まずは素直に実装してみます。
public class Fibo {
private static final int N = 50;
private static long dfsCallCount = 0;
public static void main(String args[]) {
long startTime = System.currentTimeMillis();
long fn = dfs(N);
long execTime = System.currentTimeMillis() - startTime;
System.out.println(String.format("f(%d)=%d", N, fn));
System.out.println(String.format("%dms %d回dfsを呼びました。", execTime, dfsCallCount));
}
private static long dfs(int n){
dfsCallCount++;
//不適な引数の時は-1とする(書かなくてもよい)
if(n < 0){
return -1;
}
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
return dfs(n-1) + dfs(n-2);
}
}
家のPC(いろいろアプリ起動中)で実装して動かしてみます。
f(50)=12586269025
93171ms 40730022147回dfsを呼びました。
素直に再帰で実装すると非常に時間がかかることが分かります。
ところで、よく考えてみると
再帰関数dfs(3)の計算結果はいつも同じ値2が返ってきます。
再帰関数dfs(4)の計算結果はいつも同じ値3が返ってきます。
つまり引数の値が同じときはいつも同じ値が返ってきます。
→引数をキーにして、一回計算した結果をキャッシュしてしまえば爆速になるのでは
コード
import java.util.HashMap;
public class Fibo {
private static final int N = 50;
private static long dfsCallCount = 0;
//キャッシュと言い張る
private static HashMap<Integer, Long> cache = new HashMap<Integer, Long>();
public static void main(String args[]) {
long startTime = System.currentTimeMillis();
long fn = dfs(N);
long execTime = System.currentTimeMillis() - startTime;
System.out.println(String.format("f(%d)=%d", N, fn));
System.out.println(String.format("%dms %d回dfsを呼びました。", execTime, dfsCallCount));
}
private static long dfs(int n){
dfsCallCount++;
//不適な引数の時は-1とする(書かなくてもよい)
if(n < 0){
return -1;
}
if(n == 0){
return 0;
}
if(n == 1){
return 1;
}
if(cache.containsKey(n)){
//キャッシュにあったらそれを返す
//System.out.println(String.format("%dがキャッシュにヒット!!", n));
return cache.get(n);
}else{
//キャッシュになかったら計算後、その値をキャッシュに格納
long fn = dfs(n-1) + dfs(n-2);
cache.put(n, fn);
//System.out.println(String.format("%dはキャッシュになかったので格納", n));
return fn;
}
}
}
家のPC(いろいろアプリ起動中)で実装して動かしてみます。
f(50)=12586269025
1ms 99回dfsを呼びました。
爆速になりました。
ただ、本当のキャッシュはメモリが足りなくなると使われていないデータから削除してくれる仕組みがあったりするのですが、今回使ったjavaのHashMapは本当のキャッシュではなくただの連想配列で、キーと値を対で保存してくれるだけです。メモリが足りなくなってきても解放しません。つまり難しい問題でnが莫大になっていくとメモリが足りなくなって落ちます。注意が必要です。
余談ですが、もし本気でLRUcacheなどをjavaで実装してみたい方は
googleで「LRUcache java 実装 LinkedHashMap」などを
検索して君の目で確かめてくれ・・・!
(まともな記事が見つかるかと思います)
LRUCacheを実装できたらメモ化系の問題で
とりあえずLRUCacheを使ってみて、どこまで対応できるか
やってみるのも面白いのかもしれません(無責任)
まとめ
- 深さ優先探索は終了条件付きの再帰関数で実装できる
- メモ化再帰=キャッシュ
すみませんでした。