一般的に条件分岐やループが多ければ多いほどその関数のバグの混入確率が上がると言われています。関数の複雑度を測るために循環的複雑度(cyclomatic-complexity)を用いて複雑度を数値として計測し、閾値を超えていないかをlintで検証する方法を紹介します。
(2019/01/17 追記)
前半部分はほぼ同じ内容ですが、別記事でTSLintを使った方法を別記事に書きました。
TSLintでTypeScriptの循環的複雑度(cyclomatic-complexity)を検証する - Qiita
循環的複雑度(cyclomatic-complexity)とは
一言で言えば、プログラムの複雑度です。分岐の数が多ければプログラムの実行経路は多くなり複雑度は上がります。逆に少なければ下がります。ifやforなど分岐がないプログラムの循環的複雑度は1となります。
拙いですが、以下のような関数があるとします。
function check(a, b) {
if (a >= 0) {
console.log("aは正の数です。")
} else {
console.log("aは負の数です。")
}
if (b >= 0) {
console.log("bは正の数です。")
} else {
console.log("bは負の数です。")
}
}
check(1, -1) // aは正の数です。bは負の数です。
check(-1, 1) // aは負の数です。bは正の数です。
で条件を網羅できます。
循環的複雑度の数え方は大まかに言えば「ifなどの条件分岐やforなどのループなど制御構文の数」+1した数です。
elseは含みません。
参考: Project Metrics Help - Complexity metrics
よって上記のcheck関数の循環的複雑度は3となります。
循環的複雑度の閾値
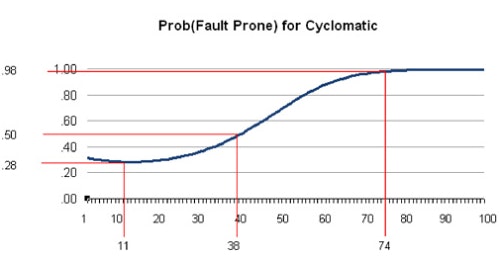
非常に古い統計データですが、循環複雑度が高ければバグは発生しやすいということは以下のグラフを見るとわかります。
| 循環的複雑度 | バグ混入確率 |
|---|---|
| 11 | 25% |
| 38 | 50% |
| 74 | 98% |
参考: Cyclomatic Complexity Revisited
循環的複雑度が10を超えるとバグ混入確率がゆるやかに上昇していっているので、1つの関数の循環的複雑度は10以内に抑えるようにコードを書くようにするといいでしょう。
ESLintでの検証
ESLintはJavaScriptの静的解析ツールです。
参考: ESLint 最初の一歩 - Qiita
ESLintには様々なルールがありますが、循環的複雑度を検証するルールも存在します。
それがcomplexityです。
ルールの設定は簡単で循環的複雑度が10を超える場合はエラーにしたい場合は以下のように設定を書きます。
{
"complexity": ["error", 10]
}
.eslintrcをyamlで書いている場合は
complexity:
- error
- 10
と書くことで循環的複雑度の設定は完了です。
設定する値はエラーレベルと閾値です。
エラーレベルは以下の3種類から設定できます。
-
off: 循環的複雑度の検証をしない -
warn: 循環的複雑度の閾値を超えると警告 -
error: 循環的複雑度の閾値を超えるとエラー
ESLintのcomplexityの閾値を10に設定した場合、循環的複雑度が11の関数があれば以下のようなエラーメッセージを出力します。
> eslint index.js
/path/to/sample-code.js
1:1 error Function 'test' has a complexity of 11 complexity
✖ 1 problem (1 error, 0 warnings)
あとがき
プログラムの複雑さを機械的に検証し、回避することでバグの混入確率だけでなく可読性も上がると思います。ぜひ、導入しましょう。
今回はJavaScriptとESLintでの検証方法を紹介しましたが、他のプログラミング言語でも循環的複雑度を検証することができる静的解析ツールはいくつかあると思いますので探してみてください。
TypeScriptとtslintを使った検証方法についても別記事で紹介したいと思います。
(2019/01/17 追記)冒頭でも紹介したとおり書きました。
TSLintでTypeScriptの循環的複雑度(cyclomatic-complexity)を検証する - Qiita
最後までお読みいただきいただきありがとうございました。質問や不備などがあればコメント欄またはTwitter(@shisama_)までお願いいたします。