過去記事で、$GF(2)$ 上の多項式 $x^{128} + x^7 + x^2 + x + 1$ が既約であることを前提に話を進めましたが、実際に既約であることを簡単に証明します。GCMを使うだけなら、まったく必要のない話ですが、気になる人のために。
手で計算することもできるはずですが、次数が大きいので、Pythonを使います。
参考文書
[1] Factoring polynomials over finite fields
https://en.wikipedia.org/wiki/Factorization_of_polynomials_over_finite_fields#External_links
[2] Berlekamp's algorithm
https://en.wikipedia.org/wiki/Berlekamp%27s_algorithm
[3]【過去記事】認証暗号化モードGCMの理論的なところの解説
https://qiita.com/shirokumaneko/items/5185373a9f0aebb16251
補足
ガロア体について
Berlekampは多項式を因数分解するアルゴリズムですが、既約かどうかを判定するだけなら簡略化できます。[1]をベースに、$GF(2)$ に特化した形で、最低限必要な箇所だけ順を追って説明します。
予備知識
今回のケースでは $q = 2$ です。つまり、$\mathbb{F}_q = \mathbb{F}_2 = GF(2) = \lbrace 0,1 \rbrace$ です。$GF(2)$ 上の多項式とは、係数が $GF(2)$ の多項式のことで、このような多項式の集合を一般に $GF(2)[x]$ や $\mathbb{F}_2[x]$ のように書きます。
$\mathbb{F}_2[x]$ では $x^7 + x^4 + x^2 + x + 1$ のように、係数が1の項のみ現れます。
(係数が0の項は書かないので)
$1 + 1 = 0, 1 = -1$ なので、$x^n + x^n = (1 + 1)x^n = 0 \cdot x = 0$ のように、同じ項を足すと0になります。また、$0^2 = 0, 1^2 = 1$ なので、$a \in GF(2) \implies (ax)^2 = ax^2$ のようになります。
任意の多項式 $f,g \in \mathbb{F}_2[x]$ に対して、$(f + g)^2 = f^2 + 2fg + g^2 = f^2 + g^2$ となります。一般に、$f,g \in \mathbb{F}_q[x]$ に対して、$(f + g)^q = f^q + g^q$ です。
補題 (Lemma 8)
$GF(2)$ 上の多項式 $f$ に対して、$f = f_1^{e_1} \cdots f_r^{e_r}$($f_i$ は既約多項式)と分解できるとすると、$g^2 \equiv g\ (\text{mod}\ f)$ となる $g$ の集合 $V$ は、$GF(2)$ 上 $r$ 次元のベクトル空間になる。
ベクトル空間であるということは
g \in V, \alpha \in GF(2) \implies \alpha g \in V \\
g,h \in V \implies g + h \in V
ということですが、前者は $\alpha = 0,1$ のみなので容易にわかります。後者も、
g^2 \equiv g, h^2 \equiv h \implies (g + h)^2 = g^2 + h^2 \equiv g + h
であることからわかります。
$r$ 次元であることを示すのは少々難解なので省略します。
この補題が意味するところは、$V = \lbrace g \in \mathbb{F}_2[x]\ |\ g^2 \equiv g\ (\text{mod}\ f) \rbrace$ の次元が1であることを言えばよいということです。その上で、$e_1 = 1$ であれば $f = f_1$、つまり $f$ 自身が既約多項式ということになります。したがって、
方針
- $r = 1$ であることを示す
- $e_1 = 1$ であることを示す
r = 1であること
$r = \text{dim}\ V$ なので、$V$ について調べます。参考文書[1]には詳しく書かれていませんが、参考文書[2]より、
g(x) = \sum_{i=0}^{127} a_i x^i
とおくと、
g(x)^2 = \sum_{i=0}^{127} a_i^2 x^{2i} = \sum_{i=0}^{127} a_i x^{2i}
$x^{2i}$ は128次以上の項を生じるので、$\text{mod}\ f$ を取って127次以下にします。
x^{2i} = \sum_{j=0}^{127} c_{ij} x^j
と表せたとすると、$Q = (c_{ij})$ は $128 \times 128$ の行列です。$g = (a_0, a_1, \cdots, a_{127})$ のように $1 \times 128$ のベクトルとみなすと、
\begin{align}
g(x)^2 &= \sum_{i=0}^{127} a_i \left(\sum_{j=0}^{127} c_{ij} x^j \right) \\
&= \sum_{j=0}^{127} \left( \sum_{i=0}^{127} a_i c_{ij} \right) x^j \\
&= \left(\sum_i a_i c_{i0}, \cdots, \sum_i a_i c_{i,128} \right) \\
&= gQ
\end{align}
$gQ$ はベクトルと行列のかけ算です。
127次以下の多項式が $\equiv 0$ なら、$= 0$ になるので、
g^2 \equiv g\ (\text{mod}\ f) \iff gQ - g = g(Q - I) = 0
つまり、
V = \text{Ker}\ (Q - I) = \lbrace g \in \mathbb{F}_2[x]\ |\ g(Q - I) = 0 \rbrace
したがって、$\text{rank}\ (Q - I) = 128 - 1 = 127$ を示せばよいことになります。
e1 = 1 であること
$f = f_1^{e_1}$ として、$\text{gcd}(f, f') = 1 \implies e_1 = 1$($f'$ は $f$ の導関数)です。
※$\text{gcd}$ = Greatest Common Divisor = 最大公約多項式
実際、$e_1 > 1$ なら $f' = e_1 f_1 f_1'$ であり、$f,f'$ とも $f_1$ で割り切れるので $\text{gcd}(f, f') = 1$ にはなり得ません。そこで、
補題 (Lemma 4)
$f,g$ を $GF(2)$ 上の多項式とする。このとき、$f = qg + r$ と書くことができ、$\text{gcd}(g,f) = \text{gcd}(g,r)$ となる。
$f = qg + r$ と書くことができるのは自明として、$f,g$ とも $h$ で割り切れるなら
\begin{align}
f &= q_1 h, g = q_2 h \\
r &= f - qg = (q_1 - qq_2)h
\end{align}
なので、$r$ も $h$ で割り切れます。つまり、$\text{gcd}(g,f)$ は $g$ と $r$ を割り切るので、$\text{gcd}(g,r)$ も割り切ります。
最後の主張
\text{gcd}(g,f)\ |\ g,\ \text{gcd}(g,f)\ |\ r \implies \text{gcd}(g,f)\ |\ \text{gcd}(g,r)
はProposition 3の内容です。なお、$a\ |\ b$ は「$a$ は $b$ を割り切る」と読みます。$a \le b$ です。
逆に $h$ が $g,r$ を割り切るなら、当然 $f$ も $h$ で割り切れます。つまり、$\text{gcd}(g,r)\ |\ \text{gcd}(g,f)$、したがって $\text{gcd}(g,f) = \text{gcd}(g,r)$ になります。
この補題を利用して、$e_1 = 1$ を示します。
Qを求める
実際に $f = x^{128} + x^7 + x^2 + x + 1$ に対して $Q$ を求めます。
まず、係数のリストで多項式のクラスを定義します。
MAX_DEGREE = 128
class GF2_Polynomial:
def __init__(self, terms=[], coef=[]) -> None:
"""
Args:
terms: 係数が1の項のリスト
"""
if terms != []:
self.coef = np.zeros(MAX_DEGREE*2, np.uint8)
for i in terms:
self.coef[i] = 1
else:
self.coef = np.array(coef)
def __str__(self):
# x^n + ... の形に文字列化する
f = GF2_Polynomial([128,7,2,1,0])
print(f)
print(f.coef)
実行結果
x^128 + x^7 + x^2 + x + 1
[1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0]
$x^{2i}$ の計算が出てくるので、128*2 = 256次元の固定長リストにしています。
多項式の割り算については、手で計算するときのことを思い出すと、例えば $f = x^7 + 1$ を $g = x^4 + x^2 + x$ で割る場合を考えると、
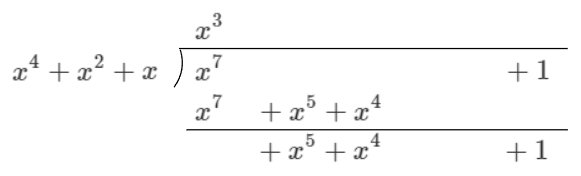
$f - x^3 g$のような計算を、余りが $< \text{deg}\ g$ になるまで繰り返していることがわかります。
$x^3$ は係数のリストを右に3個シフト、引き算は係数ごとのXORになります。
($GF(2)$ では、引き算と足し算は同じです)
こう考えると、
def residue(self, g):
r = self.coef # f
deg_r = r.nonzero()[0][-1]
deg_g = g.coef.nonzero()[0][-1]
while deg_r >= deg_g:
gtmp = np.roll(g.coef, deg_r - deg_g) # x^k・g
r = r ^ gtmp # r - x^k・g
deg_r = r.nonzero()[0][-1] if np.any(r == 1) else 0
return GF2_Polynomial(coef=r)
deg_gは固定ですが、deg_rはwhileをまわるたびに小さくなり、最終的にdeg_r < deg_gになります。
試しに、
f = GF2_Polynomial([7,0]) # x^7 + 1
g = GF2_Polynomial([4,2,1]) # x^4 + x^2 + x
r = f.residue(g)
print(r)
実行結果
x^3 + x + 1
手で計算すれば、同じ結果が得られます。
これより、
def square_residue_matrix(f):
deg = f.coef.nonzero()[0][-1]
Q = np.zeros((deg,deg), np.uint8)
for i in range(deg):
x2i = GF2_Polynomial([2*i]) # x^{2i}
r = x2i.residue(f) # x^{2i} mod f
Q[i] = r.coef[:deg]
return Q
f = GF2_Polynomial([128,7,2,1,0])
Q = square_residue_matrix(f)
print(Q)
実行結果
[[1 0 0 0 0 ... 0 0 0 0 0]
[0 0 1 0 0 ... 0 0 0 0 0]
[0 0 0 0 1 ... 0 0 0 0 0]
[0 0 0 0 0 ... 0 0 0 0 0]
[0 0 0 0 0 ... 0 0 0 0 0]
...
[0 0 0 0 0 ... 0 0 1 0 0]
[0 0 0 0 0 ... 0 0 0 0 1]
[0 1 1 1 0 ... 1 1 0 0 0]
[0 0 0 1 1 ... 0 1 1 1 0]
[1 1 1 0 0 ... 0 0 0 1 1]]
rank (Q - I)を求める
I = np.identity(128, np.uint8)
Q_I = Q ^ I
ガウスの消去法でrankを求めます。大雑把な手順としては、
$Q - I$ の $j$ 列( $j = 1,2,\cdots,128$ )について、
- ピボット($j$ 列が1の行)を選択する
- ピボット行と $j$ 行を入れ替える
- $j$ 列の1を消去する
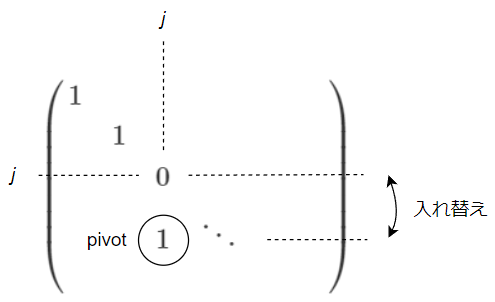
ただし、ピボットが存在しない列はスキップします。ピボットが存在する列の数が $\text{rank}$ になります。
def gaussian_elimination(M):
"""
Args:
M: GF(2)の2-dim ndarray
"""
nrow = M.shape[0]
ncol = M.shape[1]
rank = 0
for column in range(ncol):
for row in range(rank,nrow):
if M[row][column] == 1: # ピボットを選択する
tmp = M[row].copy() # ピボット行と j 行を入れ替える
M[row] = M[rank]
M[rank] = tmp
break
else:
continue # ピボットが存在しない列はスキップ
for row in range(rank+1,nrow):
if M[row][column] == 1:
M[row] ^= M[rank] # j 列の1を消去する
rank += 1
return rank
rank = gaussian_elimination(Q_I)
print(Q_I)
print(rank)
実行結果
[[1 1 1 0 0 ... 0 0 0 0 0]
[0 1 1 0 0 ... 0 0 0 0 0]
[0 0 1 0 1 ... 0 0 0 0 0]
[0 0 0 1 0 ... 0 0 0 0 0]
[0 0 0 0 1 ... 0 0 0 0 0]
...
[0 0 0 0 0 ... 1 0 1 0 0]
[0 0 0 0 0 ... 0 1 0 0 0]
[0 0 0 0 0 ... 0 0 1 1 0]
[0 0 0 0 0 ... 0 0 0 1 0]
[0 0 0 0 0 ... 0 0 0 0 0]]
127
省略されていますが、最後の行はすべて0になっています。
これで、$r = 1$ であることが示されました。
gcd(f, f')を求める
\begin{align}
f &= x^{128} + x^7 + x^2 + x + 1 \\
f' &= x^6 + 1
\end{align}
$GF(2)$ の微分も実数の場合と同様ですが、$128x^{127} = 0x^{127} = 0, 7x^6 = 1x^6 = x^6$ のように、係数を $0,1$ に直す必要があります。
f = GF2_Polynomial([128,7,2,1,0]) # f = x^{128} + x^7 + x^2 + x + 1
df = GF2_Polynomial([6,0]) # f'= x^6 + 1
r = f.residue(df)
print(r)
実行結果
1
つまり、$f = qf' + 1$ です。Lemma 4より、$\text{gcd}(f, f') = \text{gcd}(f', 1) = 1$ になります。
これで、$e_1 = 1$ が示されました。
結論
$r = 1, e_1 = 1$ なので、$x^{128} + x^7 + x^2 + x + 1$ が既約多項式であることが証明されました。
補足
Qとガウスの消去法のテスト
手で計算できるパターンとして、Example 10の$f = x^7 + x^4 + x^2 + x + 1$ に対して、それぞれ単体テストします。この場合、$Q$ は $7 \times 7$ の行列で
\begin{align}
Q[0] = x^0 &= [1,0,0,0,0,0,0] \\
Q[1] = x^2 &= [0,0,1,0,0,0,0] \\
Q[2] = x^4 &= [0,0,0,0,1,0,0] \\
Q[3] = x^6 &= [0,0,0,0,0,0,1] \\
Q[4] = x^8 &= x(x^4 + x^2 + x + 1) \\
&= x^5 + x^3 + x^2 + x \\
&= [0,1,1,1,0,1,0] \\
Q[5] = x^{10} &= x^3(x^4 + x^2 + x + 1) \\
&= x^7 + x^5 + x^4 + x^3 \\
&= (x^4 + x^2 + x + 1) + x^5 + x^4 + x^3 \\
&= x^5 + x^3 + x^2 + x + 1 \\
&= [1,1,1,1,0,1,0] \\
Q[6] = x^{12} &= x^5(x^4 + x^2 + x + 1) \\
&= x^9 + x^7 + x^6 + x^5 \\
&= x^2(x^4 + x^2 + x + 1) + (x^4 + x^2 + x + 1) + x^6 + x^5 \\
&= x^5 + x^3 + x + 1 \\
&= [1,1,0,1,0,1,0]
\end{align}
つまり、
Q = \left(
\begin{array}{ccccccc}
1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 1 & 1 & 1 & 0 & 1 & 0 \\
1 & 1 & 1 & 1 & 0 & 1 & 0 \\
1 & 1 & 0 & 1 & 0 & 1 & 0
\end{array}
\right)
import unittest
class TestBerlekamp(unittest.TestCase):
def test_q(self):
f = GF2_Polynomial([7,4,2,1,0])
Q = square_residue_matrix(f)
Q_exp = np.array([[1,0,0,0,0,0,0],
[0,0,1,0,0,0,0],
[0,0,0,0,1,0,0],
[0,0,0,0,0,0,1],
[0,1,1,1,0,1,0],
[1,1,1,1,0,1,0],
[1,1,0,1,0,1,0]])
self.assertEqual(np.array_equal(Q, Q_exp), True)
また、
Q - I = \left(
\begin{array}{ccccccc}
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 1 & 1 & 1 & 1 & 1 & 0 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 \\
1 & 1 & 0 & 1 & 0 & 1 & 1
\end{array}
\right)
にガウスの消去法を適用すると
\downarrow \\
\left(
\begin{array}{ccccccc}
1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 1 & 1 & 1 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 1 & 1
\end{array}
\right) \\
\downarrow \\
\left(
\begin{array}{ccccccc}
1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 1 & 1
\end{array}
\right) \\
\downarrow \\
\left(
\begin{array}{ccccccc}
1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 & 1
\end{array}
\right) \\
\downarrow \\
\left(
\begin{array}{ccccccc}
1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 1 & 1
\end{array}
\right) \\
\downarrow \\
\left(
\begin{array}{ccccccc}
1 & 1 & 1 & 1 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0
\end{array}
\right)
これより、rank 5であることがわかります。
def test_qi(self):
Q = np.array([[1,0,0,0,0,0,0],
[0,0,1,0,0,0,0],
[0,0,0,0,1,0,0],
[0,0,0,0,0,0,1],
[0,1,1,1,0,1,0],
[1,1,1,1,0,1,0],
[1,1,0,1,0,1,0]])
I = np.identity(7, np.uint8)
Q_I = Q ^ I
Q_I_exp = np.array([[1, 1, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0, 1],
[0, 0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])
rank = gaussian_elimination(Q_I)
self.assertEqual(np.array_equal(Q_I, Q_I_exp), True)
self.assertEqual(rank, 5)
実行結果
Ran 2 tests in 0.001s
OK
x^7 + x^4 + x^2 + x + 1 の因数分解
GCMからは完全に外れますが、既約でない場合も試してみます。
Example 10より $x^7 + x^4 + x^2 + x + 1 = (x^2 + x + 1)^2 (x^3 + x + 1)$ ですが、計算でこの結果を導きます。
補題(Lemma 7)
$f$ を $GF(2)$ 上の多項式とする。また、$g$ を $g^2 \equiv g\ (\text{mod}\ f)$ となるような $GF(2)$ 上の多項式とする。このとき、
$$f = \prod_{a \in \mathbb{F}_2} \text{gcd}(f, g - a) = \text{gcd}(f, g) \cdot \text{gcd}(f, g + 1)$$
$g^2 \equiv g\ (\text{mod}\ f)$ は $g^2 - g$ が $f$ で割り切れるということですが、これは $f$ 自身が $f$ と $g^2 - g$ のGCDになるということです。
f = \text{gcd}(f, g^2 - g)
$g^2 - g = g(g - 1) = g(g + 1)$ なので ※$GF(2)$ では $-1 = 1$
\begin{align}
f &= \text{gcd}(f, g^2 - g) \\
&= \text{gcd}(f, g(g + 1)) \\
&= \text{gcd}(f, g) \cdot \text{gcd}(f, g + 1)
\end{align}
最後の=は、任意の $g$ に対して $g$ と $g + 1$(定数項だけが異なる多項式)は互いに素であることから出てきます。
この補題により、$f$ の因数分解が得られます。$\text{gcd}(f, g)$ と $\text{gcd}(f, g + 1)$ が既約なら、これで完了です。既約でなければ、同じ手順で分解していけばよいです。
そこで、$f = x^7 + x^4 + x^2 + x + 1$ における $g$ を求めます。
(既約のときは $g = 1$ のみです)
$g(Q - I) = 0$ を $(Q - I)^T g^T = 0$ と書き直し、$(Q - I)^T = Q^T - I$ をrow reduced echelon form(RREF)に変形します。RREFとは大雑把に言うと、
\left(
\begin{array}{cc}
I & * \\
0 & 0 \\
\end{array}
\right)
のような形の行列で、もう少し正確に言うと
- 各行のピボット(左から見ていって初めて1が現れる箇所)は、直前の行よりも右に来る
- 要素がすべて0の行は下に現れる
したがって、
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0 \\
\end{array}
\right),
\left(
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0 \\
\end{array}
\right)
などもRREFになります。
RREFへの変形は、ガウスの消去法の延長です。ガウスの消去法では、ピボット行から下の1だけを消去していましたが、消去の範囲を行全体に広げます。つまり、
def gaussian_elimination(M):
...(略)...
# for row in range(rank+1,nrow): # ガウスの消去法
for row in range(nrow): # RREF 行全体
if row != rank: # ピボット行自身は除く
if M[row][column] == 1:
M[row] ^= M[rank]
Q = square_residue_matrix(f)
I = np.identity(f.degree(), np.uint8)
Q_I = (Q ^ I).transpose()
gaussian_elimination(Q_I)
print(Q_I)
実行結果
[[0 1 0 0 0 0 1]
[0 0 1 0 0 0 1]
[0 0 0 1 0 0 1]
[0 0 0 0 1 0 1]
[0 0 0 0 0 1 1]
[0 0 0 0 0 0 0]
[0 0 0 0 0 0 0]]
Q^T - I = \left(
\begin{array}{ccccccc}
0 & 1 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
\right)
RREFに変形出来たら、$= 0$ の解は簡単に求まります。$g = (0,1,1,1,1,1,1)$ に対して $(Q^T - I) g^T$ を計算してみると、どの行も $1 + 1 = 0$ できれいに0になることがわかると思います。
(一般的な手順はありますが、省略します)
この $g$ は、$x^6 + x^5 + x^4 + x^3 + x^2 + x$ に相当します。つまり、
f = \text{gcd}(f, x^6 + x^5 + x^4 + x^3 + x^2 + x) \cdot \text{gcd}(f, x^6 + x^5 + x^4 + x^3 + x^2 + x + 1)
gcdを求める
$x^{128} + x^7 + x^2 + x + 1$ の場合は、$f = qf' + 1$ となってGCDを簡単に求められましたが、一般にはLemma 4を繰り返し適用します。いわゆる、ユークリッドの互除法です。
\begin{align}
f = q_1 g + r_1 &\implies \text{gcd}(g,f) = \text{gcd}(g,r_1) \\
g = q_2 r_1 + r_2 &\implies \text{gcd}(g,r_1) = \text{gcd}(r_1,r_2) \\
&\ \ \ \ \ \vdots
\end{align}
def gcd(f, g):
r1 = f
r2 = f.residue(g)
while r2.degree() > 0:
r = r1.residue(r2)
r1 = r2
r2 = r
return r1
f = GF2_Polynomial([7,4,2,1,0])
g = GF2_Polynomial([6,5,4,3,2,1])
r = gcd(f, g)
print(r)
g = GF2_Polynomial([6,5,4,3,2,1,0])
r = gcd(f, g)
print(r)
実行結果
x^4 + x^2 + 1
x^3 + x + 1
これより、
\begin{align}
f &= (x^4 + x^2 + 1) (x^3 + x + 1) \\
&= (x^2 + x + 1)^2 (x^3 + x + 1)
\end{align}
が得られました。