線形計画問題
線形計画問題とは目的関数、制約条件がともに線形の形で表されており、以下のようなベクトル${\bf x}$を最小化する問題として表現されます。
\min {\bf c}^T{\bf x}
\\subject \ \ {\bf A}{\bf x}\le {\bf b}
ここで${\bf x}$の次元を$n$、制約数を$m$とすると、${\bf x},{\bf c}, {\bf b}$は$n$次元ベクトル、${\bf A}$は$m \times n$の行列です。
カーマーカー法
線形計画問題の解法として単体法というものが古くからあるのですが、大規模な問題では効率が悪く、そちらでは今回紹介する内点法が用いられています。
線形計画における内点法では、カーマーカー法というアルゴリズムがかなり有名です。このアルゴリズムはソフトウェア界の特許の話でもよく出てくる話で、コードにしてもとてもシンプルに書けて、美しいアルゴリズムだと言われています。
以下がpythonで記述したカーマーカー法の関数です。
# !/usr/bin/python
# coding:utf-8
import numpy as np
def karmarkar_method(x, c, amat, b,
gamma=1.0, eps=1.0e-3, nloop=30):
"""
Karmarkar法による線形計画問題の解法
object min z = c^T * x
subject Ax <= b
"""
for n in range(nloop):
vk = b - amat * x
gmat = amat.T * np.diag(1.0 / np.square(vk.A1)) * amat
d = np.linalg.pinv(gmat) * c
if np.linalg.norm(d) < eps:
break
hv = -amat * d
if np.max(hv) <= 0:
print("Unbounded!")
x = None
break
alpha = gamma * np.min(vk[hv > 0] / hv[hv > 0])
x -= alpha * d
yield x
#return x
if __name__ == "__main__":
c = np.matrix([[-1.0],
[-1.0]])
amat = np.matrix([[1.0, 1.0],
[1.0, -1.0]])
b = np.matrix([[0.5],
[1.0]])
# 描画
from pylab import *
ax = subplot(111, aspect='equal')
x = np.arange(-3.0, 3.01, 0.15)
y = np.arange(-3.0, 3.01, 0.15)
X,Y = meshgrid(x, y)
t = np.arange(-3.0, 3.01, 0.15)
func = lambda x, y : c[0, 0] * x + c[1, 0] * y
const = [lambda x : -amat[0, 0] / amat[0, 1] * x + b[0, 0] / amat[0, 1],
lambda x : -amat[1, 0] / amat[1, 1] * x + b[1, 0] / amat[1, 1]]
Z = func(X, Y)
s = [const[i](t) for i in range(2)]
pcolor(X, Y, Z)
for i in range(2):
ax.plot(t, s[i], 'k')
for x in karmarkar_method(np.matrix([[-2.0], [-2.0]]), c, amat, b, gamma=0.5, eps=1.0e-3, nloop=30):
print(x)
ax.plot([x[0,0]], [x[1,0]],'ro')
axis([-3, 3, -3, 3])
show()
今回は描画用に最小値だけでなく途中経過も返すようにしています。
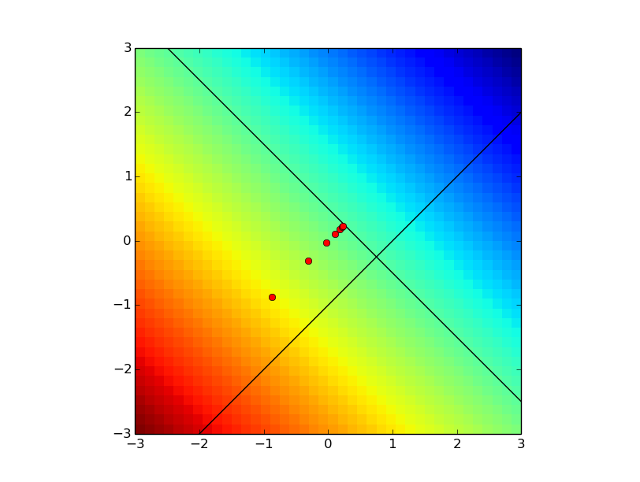
以下に最小値に向かう様子の図を示します。
青い領域が目的関数が小さくなる領域を示していて、赤い点が青い方向に向かいつつ、制約となっている線の手前でストップしているのが分かります。
現在、内点法は二次計画問題や非線形計画問題にも用いられていますが、カーマーカー法はその先駆けとも言えるアルゴリズムなのですね。