Scipyで見つけた数学関数あれこれ

2015年を振り返ってscipyで見つけた数学関数あれこれをまとめたいと思います。

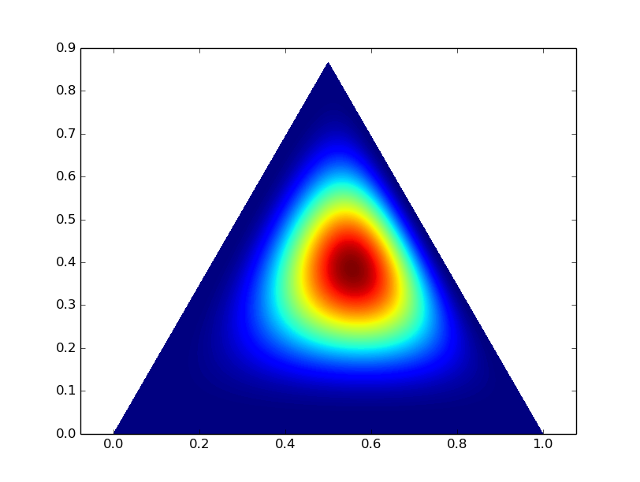
scipy.stats.dirichlet

LDAなどで使われるディリクレ分布の関数です。

import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import matplotlib.tri as tri

alphas = np.array([3.0, 4.0, 5.0])
dc = ss.dirichlet(alphas)

corners = np.array([[0.0, 0.0], [1.0, 0.0], [0.5, np.sqrt(3.0) / 2.0]])
midpoints = [(corners[(i + 1) % 3] + corners[(i + 2) % 3]) / 2.0 for i in range(3)]

def xy2bc(xy):
    s = [(corners[i] - midpoints[i]).dot(xy - midpoints[i]) / 0.75 for i in range(3)]
    return np.clip(s, 0.0, 1.0)
refiner = tri.UniformTriRefiner(tri.Triangulation(corners[:, 0], corners[:, 1]))
trimesh = refiner.refine_triangulation(subdiv=8)
pvals = [dc.pdf(xy2bc(xy)) for xy in zip(trimesh.x, trimesh.y)]
plt.tricontourf(trimesh, pvals, 200)
plt.axis('equal')
plt.show()

scipy.stats.wishert, scipy.stats.invwishert

こちらもMCMC等で使われることのあるウィシャート分布と逆ウィシャート分布です。
以下の例では、2次元の分散行列の乱数をそれぞれ10個生成します。

import numpy as np
import scipy.stats as ss

w = ss.wishart(df=3, scale=np.matrix([[1.0, 0.5], [0.5, 1.0]]))
print w.rvs(10)
iw = ss.invwishart(df=3, scale=np.matrix([[1.0, 0.5], [0.5, 1.0]]))
print iw.rvs(10)

scipy.special.comb, scipy.special.perm

順列と組み合わせの計算です。

>>> import scipy.special as ss
>>> ss.comb(6, 3) # 6C3
20.0
>>> ss.perm(6, 3) # 6P3
120.0

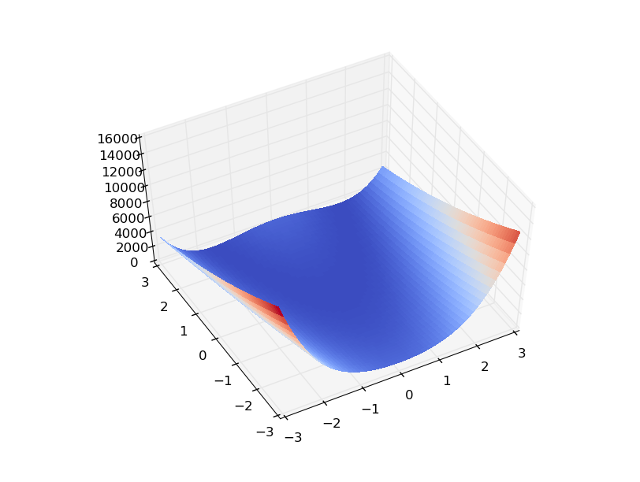
scipy.optimize.rosen

最適化のお題で使われるローゼンブロック関数です。

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import matplotlib.pyplot as plt

from scipy.optimize import rosen
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')
X, Y = np.meshgrid(np.arange(-3., 3., 0.1), np.arange(-3., 3., 0.1))
Z = [[rosen((x, y)) for x, y in zip(xx, yy)] for xx, yy in zip(X, Y)]
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm, linewidth=0, antialiased=False)
plt.show()

scipy.signal.lti

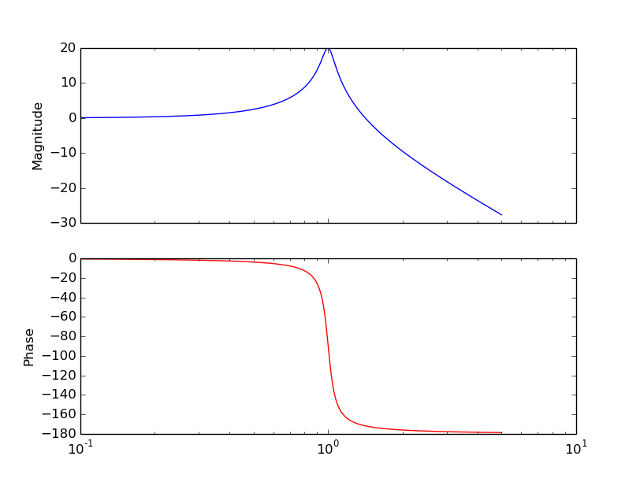
制御工学でお世話になる線形時不変システム(Linear Time Invariant)です。
以下の例では線形時不変システムを作成し、そのボード線図を描画しています。

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

# 1 / s^2 + 0.1s + 1
s = signal.lti([1], [1.0, 0.1, 1.0])
w, mag, phase = signal.bode(s, np.arange(0.1, 5.0, 0.01).tolist())

fig, (ax0, ax1) = plt.subplots(nrows=2, sharex=True)
ax0.semilogx(w, mag, 'b-')
ax0.set_ylabel("Magnitude")
ax1.semilogx(w, phase, 'r-')
ax1.set_ylabel("Phase")
plt.show()

scipy.spatial.KDTree

空間分割アルゴリズムのKDツリーです。
以下の例では3次元空間にグリッド状に点をばらまき、(20,20,20)の点から1.0の距離範囲にいる点をすべて抽出しています。

import numpy as np
import scipy.spatial as ss                                      

x, y, z= np.mgrid[0:100, 0:100, 0:100]
points = zip(x.ravel(), y.ravel(), z.ravel())
tree = ss.KDTree(points)
a = tree.query_ball_point([20, 20, 20], 1.0)
print [points[i] for i in a]

[(19, 20, 20), (20, 19, 20), (20, 20, 19), (20, 20, 20), (20, 20, 21), (20, 21, 20), (21, 20, 20)]

scipy.cluster.vq.kmeans2

クラスタリングアルゴリズムのk平均法です。

import numpy
from scipy.cluster.vq import kmeans2, whiten

features = numpy.array([[ 1.9,2.3],
                        [ 1.5,2.5],
                        [ 0.8,0.6],
                        [ 0.4,1.8],
                        [ 0.1,0.1],
                        [ 0.2,1.8],
                        [ 2.0,0.5],
                        [ 0.3,1.5],
                        [ 1.0,1.0]])
wf = whiten(features)  # 正規化
print kmeans2(wf, k=2)

中心地と各値のラベルが得られます。

(array([[ 1.40584568,  0.69587293],
       [ 1.24002799,  2.50514254]]), array([1, 1, 0, 1, 0, 1, 0, 1, 0]))

scipy.constants.g

関数ではないですが、重力加速度です。他にもいろんな物理パラメタが定義されています。

>>> import scipy.constants
>>> scipy.constants.g
9.80665

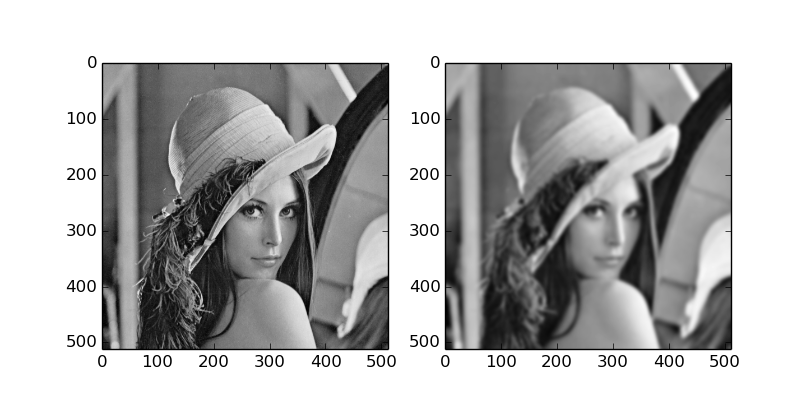
scipy.ndimage.gaussian_filter

画像処理で使われるフィルタアルゴリズムです。

import scipy
from scipy import ndimage
import matplotlib.pyplot as plt

img = scipy.misc.lena().astype(float)
fimg = ndimage.gaussian_filter(img, 3)

plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.imshow(img, cmap=plt.cm.gray)
plt.subplot(122)
plt.imshow(fimg, cmap=plt.cm.gray)
plt.show()

まとめ

scipyはいろんな分野のいろんな関数やアルゴリズムが実装されていて、リファレンスを眺めているだけでも楽しいですね。来年もお世話になります。