Symbolic Regression
前回投稿したPythonの進化計算ライブラリDeapの紹介の続きです。今回は遺伝的プログラミング(GP)のExampleの中にあるSymbolic Regressionを見ていきます。
GPは遺伝的アルゴリズム(GA)の遺伝子型を木構造やグラフ構造で扱えるようにしたもので、Symbolic RegressionはGPの代表的な問題です。具体的な内容は以下の4次関数を$[-1, 1]$の範囲で同定する問題です。
f(x)=x^4+x^3+x^2+x
評価関数は-1から1の間の20個の点における推定した式$prog(x)$と真の式$f(x)$との誤差で表現します。
\sum_{i=1}^{20} |prog(x_i) - f(x_i)|^2
それでは実際にExampleの中身を見ていきます。
まずはモジュールのインポートです。
import operator
import math
import random
import numpy
from deap import algorithms
from deap import base
from deap import creator
from deap import tools
from deap import gp
次に木構造の各ノードとなるプリミティブの集合を作成します。ここでは基本的な算術演算や三角関数、一時的な乱数が集合に含まれています。
# Define new functions
def safeDiv(left, right):
try:
return left / right
except ZeroDivisionError:
return 0
pset = gp.PrimitiveSet("MAIN", 1)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.sub, 2)
pset.addPrimitive(operator.mul, 2)
pset.addPrimitive(safeDiv, 2)
pset.addPrimitive(operator.neg, 1)
pset.addPrimitive(math.cos, 1)
pset.addPrimitive(math.sin, 1)
pset.addEphemeralConstant("rand101", lambda: random.randint(-1,1))
pset.renameArguments(ARG0='x')
ゼロ割りによるエラーを防ぐために新規に割り算を定義し直してプリミティブに追加しており、その他はpythonのoperatorモジュールとmathモジュールの関数を使っています。addPrimitiveの2つ目の引数はプリミティブ関数の引数の数を示しています。
addEphemeralConstantはノードの終端において、定数ではなく乱数などの関数から生成される値を用いる場合に使用します。ここでは-1,0,1のどれかを生成する乱数を定義しているのが分かります。今回の問題ではあまり選ばれなさそうな気もしますが…
PrimitiveSetの2つ目の引数はプログラムの入力の数を示しています。今回は1つで、デフォルトでは"ARG0"と名付けられるのですが、renameArgumentsで"x"という名前に変更しています。
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMin)
次に前回のGAの例と同様に creator で最小化問題の設定と個体の型の設定を行います。
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
def evalSymbReg(individual, points):
# tree表現から関数への変換
func = toolbox.compile(expr=individual)
# 推定式と真の式との平均平方誤差の計算
sqerrors = ((func(x) - x**4 - x**3 - x**2 - x)**2 for x in points)
return math.fsum(sqerrors) / len(points),
toolbox.register("evaluate", evalSymbReg, points=[x/10. for x in range(-10,10)])
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=0, max_=2)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)
次に toolbox を用いて個体および個体群の生成方法、評価関数、交差、突然変異、選択方法等を作成していきます。gp.genHalfAndHalfは木の生成を行う関数なのですが、min_およびmax_で木の深さの最小と最大を指定し、genGrow(それぞれの葉ノードの深さが異なってよい木の生成)とgenFull(それぞれの葉ノードの深さが同じ木の生成)を半々に行うようになっています。gp.compileは個体から実際に実行できる関数の生成を行います。
最後の方では突然変異をノードに新たなサブツリーを追加するという方法で指定しています。
def main():
random.seed(318)
pop = toolbox.population(n=300)
hof = tools.HallOfFame(1)
stats_fit = tools.Statistics(lambda ind: ind.fitness.values)
stats_size = tools.Statistics(len)
mstats = tools.MultiStatistics(fitness=stats_fit, size=stats_size)
mstats.register("avg", numpy.mean)
mstats.register("std", numpy.std)
mstats.register("min", numpy.min)
mstats.register("max", numpy.max)
pop, log = algorithms.eaSimple(pop, toolbox, 0.5, 0.1, 40, stats=mstats,
halloffame=hof, verbose=True)
# logの表示
return pop, log, hof
if __name__ == "__main__":
main()
次にmain関数を作り、実行します。最初に統計情報を得るために計算したい統計情報の設定をしており、次に初期の個体群を生成し、eaSimpleで進化計算を行います。
実行すると以下のように各世代での統計情報が出力されます。
fitness size
--------------------------------------- -------------------------------
gen nevals avg max min std avg max min std
0 300 2.36554 59.2093 0.165572 4.63581 3.69667 7 2 1.61389
1 146 1.07596 10.05 0.165572 0.820853 3.85333 13 1 1.79401
2 169 0.894383 6.3679 0.165572 0.712427 4.2 13 1 2.06398
3 167 0.843668 9.6327 0.165572 0.860971 4.73333 13 1 2.36549
4 158 0.790841 16.4823 0.165572 1.32922 5.02 13 1 2.37338
5 157 0.836829 67.637 0.165572 3.97761 5.59667 13 1 2.20771
6 179 0.475982 3.53043 0.150643 0.505782 6.01 14 1 2.02564
7 176 0.404081 2.54124 0.150643 0.431554 6.42 13 1 2.05352
8 164 0.39734 2.99872 0.150643 0.424689 6.60333 14 3 2.10063
9 161 0.402689 13.5996 0.150643 0.860105 6.61333 13 3 2.05519
10 148 0.392393 2.9829 0.103868 0.445793 6.74333 15 1 2.39669
11 155 0.39596 7.28126 0.0416322 0.578673 7.26333 15 1 2.53784
12 163 0.484725 9.45796 0.00925063 0.733674 8.16 17 1 2.74489
13 155 0.478033 11.0636 0.0158757 0.835315 8.72333 21 1 3.04633
14 184 0.46447 2.65913 0.0158757 0.562739 9.84333 23 1 3.17681
15 161 0.446362 5.74933 0.0158757 0.700987 10.5367 23 2 3.29676
16 187 0.514291 19.6728 0.013838 1.44413 11.8067 25 1 4.25237
17 178 0.357693 3.69339 0.00925063 0.456012 12.7767 29 1 5.3672
18 163 0.377407 14.2468 0.00925063 0.949661 13.4733 35 1 5.67885
19 155 0.280784 9.55288 0.00925063 0.691295 15.2333 36 2 5.7884
20 165 0.247941 2.89093 0.00925063 0.416445 15.63 31 3 5.66508
21 160 0.229175 2.9329 0.00182347 0.406363 16.5033 37 2 6.44593
22 165 0.183025 3.07225 0.00182347 0.333659 16.99 32 2 5.77205
23 156 0.22139 2.49124 0.00182347 0.407663 17.5 42 1 6.7382
24 167 0.168575 1.98247 5.12297e-33 0.272764 17.48 43 3 6.21902
25 166 0.177509 2.3179 5.12297e-33 0.330852 16.9433 36 1 6.6908
26 152 0.187417 2.75742 5.12297e-33 0.382165 17.2267 47 3 6.21734
27 169 0.216263 3.37474 5.12297e-33 0.419851 17.1967 47 3 6.00483
28 176 0.183346 2.75742 5.12297e-33 0.295578 16.7733 42 3 5.85052
29 159 0.167077 2.90958 5.12297e-33 0.333926 16.59 45 2 5.75169
30 171 0.192057 2.75742 5.12297e-33 0.341461 16.2267 53 3 5.48895
31 209 0.279078 3.04517 5.12297e-33 0.455884 15.84 32 3 5.60188
32 161 0.291415 19.9536 5.12297e-33 1.22461 16.0267 35 3 5.45276
33 157 0.16533 2.54124 5.12297e-33 0.316613 15.5033 33 2 5.08232
34 159 0.164494 2.99681 5.12297e-33 0.316094 15.4567 33 1 4.99347
35 157 0.158183 2.9829 5.12297e-33 0.309021 15.3133 34 2 4.54113
36 172 0.203184 3.00665 5.12297e-33 0.380584 15.12 29 1 4.70804
37 181 0.251027 4.66987 5.12297e-33 0.483365 15.18 36 1 5.6587
38 141 0.249193 12.8906 5.12297e-33 0.848809 15.1633 36 1 5.38114
39 158 0.188209 2.33071 5.12297e-33 0.346345 15.1967 32 1 4.82887
40 165 0.220244 2.3179 5.12297e-33 0.381864 15.44 33 2 5.70787
expr = toolbox.individual()
nodes, edges, labels = gp.graph(expr)
import matplotlib.pyplot as plt
import networkx as nx
g = nx.Graph()
g.add_nodes_from(nodes)
g.add_edges_from(edges)
pos = nx.graphviz_layout(g, prog="dot")
nx.draw_networkx_nodes(g, pos)
nx.draw_networkx_edges(g, pos)
nx.draw_networkx_labels(g, pos, labels)
plt.show()
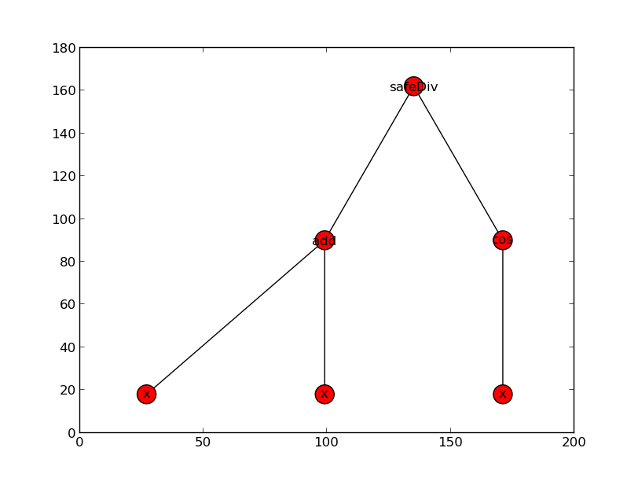
最後に最終的に最適化された木の描画も行ってみます。描画にはnetworkxとmatplotlibを用いています。
以下が今回の最適化で得られた木の構造です。
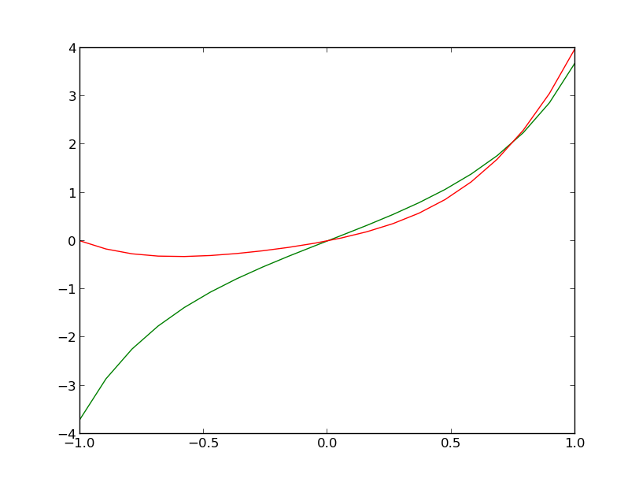
実際に近い関数が本当に得られたかをグラフにしてちょっと確認してみます。
赤が真の関数で緑が推定結果なのですが、なんかイマイチです。木の深さやプリミティブを他にも追加することで改善されるかもしれませんが、とりあえず今回はここまでにしておきます。
参考
Symbolic RegressionのExample:http://deap.gel.ulaval.ca/doc/dev/examples/gp_symbreg.html