はじめに
以下の記事のDFFの設計のあたりを読んで、自分でも設計をしてみたくなったので、3連休中の設計・実装の結果をまとめておきます。
大学でコンピューターサイエンスを専攻したわけではなく、独学で色々調べて考察した結果なので、一部間違っているかもしれません。
魔法を解く
現代のコンピューターは魔法と呼んでも十分な程に高度化してしまい、内部を理解することは容易ではありません。
実際に私はプログラムを書いて給料をもらっていますが、自分の書いたプログラムが最終的にどのようにして電気信号や光信号といった物理的な実体に対応付いているのかと聞かれたら、正直なところ正確に答えられる自信がないです。
このようにして魔法のようになってしまったコンピューターの内部構造を理解するためにどうすれば良いかというと、自分が確実に理解できるものからボトムアップ的に高度なものを組み上げていくのが一番の近道です。
では、この確実に理解できる「何か」を何にするべきでしょうか。
最近のコンピューターのほぼすべては半導体(特にCMOS)で作られていますが、半導体のことをしっかり理解できているかと聞かれたら怪しいです。
大学の授業で半導体中の電子のバンド構造の計算をしましたが、確実に理解できたかと言われたらNoとなってしまいます。
最近のコンピューターのほぼすべては半導体(特にCMOS)で作られていますが、実は昔はそれ以外の素子を使って作られていました。
例えば真空管やパラメトロンなどです。
これらの仕組みも調べてみたらそこそこ複雑だったので、一旦NGとしておきます。
十分にシンプルで、小学校の理科の知識くらいでも理解できるような素子はないかと思い探していたらありました。
リレーです。
コイルに電流を流すと磁気を帯び、その磁気を使って鉄片を引き寄せることでスイッチングをするという素子です。
小学校の理科の時間に手巻きのコイルを作ったことがある人は多いかと思います。
そのコイルの近くに鉄片とバネを配置すれば簡易的なリレーの出来上がりです。
これならば十分にシンプルな素子なので、これを基本的なビルディングブロックにして話を進めます。
※ この話もなんでコイルに電気を流すと磁気が生じるのかという部分の理解は実はあやふやで、マクスウェル方程式を完全に理解しているわけではないのですが、一旦そこには目をつむります。
論理ゲートづくりの鬼門
基本素子が決まればあとはそれを使って論理ゲートを作り、それらを使ってカウンタや加算器などの更に複雑な機能を持ったブロックを作り、更にそれらを使ってALUや命令デコーダーなどを作っていけば最終的にCPUに到達します。
ですが、この論理ゲート作りで一番難しいのはDFFの作成です。
ANDやORなどの論理ゲートは簡単に思いつくことができる一方で、順序回路の基礎となるDFFはなかなかに作成するのが難しいです。
ですので、この記事ではDFF作成を順を追って説明していきたいと思います。
縛りプレイ
DFFを作成するにあたって、以下の制約を課します。
- 使用できる素子はリレーのみ
この制約により、トランジスタやダイオードなどの半導体はもちろん、抵抗やコンデンサなどの受動素子の利用もNGになります。
そのため、信号のタイミングを遅延させるためにCR回路を使うといったことはできません。
ただし、例外的に以下のものは使用を認めるものとしています。
- 表示用のLED & 電流制限抵抗
- 直流電源回路(ACアダプタ)の中の半導体
ハシゴで回路を表現する
リレーを使った回路図を表現するためにラダー図を使用します。
ラダー図はリレー回路やシーケンス制御のときに使われる図で、リレーやスイッチの繋がりをシンプルに表現できます。
例えば、上の図ではCR1がリレー、Inが入力、Out1, 2が出力を表しています。
そして左にある長い縦線はプラスの電圧、右の縦線は0Vを表しています。
図中のCR1は3種類ありますが、 ( ) はリレーのコイルを表しており、 | | はコイルに電流を流すと繋がる接点(Make接点・a接点)を、 Nを鏡に映したようなもの はコイルに電流を流すと繋がる接点(Break接点・b接点)を表しています。そのため、Out1はInをバッファしたものであり、Out2はInを反転したものになります。
リレーの接点は他の接点と直列・並列に接続することもできます。
ラダー図でAND回路を書くとこのようになります。
2つのリレーが直列につながっていることでANDを表現しています。
このような表現を使うことで実体配線図を書くよりもシンプルにリレー回路を表現できます。
自己保持回路(自分自身に電流を流す)
ここからラダーを使って回路を書いていきます。
一番最初に紹介するのは自己保持回路です。
今後登場するすべての回路の基礎となる回路です。
CR1のa接点とコイルが接続されています。
そのため、一旦InをONにしてCR1に電流が流すと、その後は電源を切るまでずっとCR1に電流が流れ続けます。
この回路は過去に1回以上InがONになったことがあるかどうかという状態を保持しているとも言えます。
RSフリップフロップ(リセット機能を付与)
自己保持回路は状態のリセットができないという欠点があったため、リセット機能もつけましょう。
CR1に直列に接点を入れて、自己保持中の電流をOFFにできるようにします。
これがいわゆるRSフリップフロップです。
R(Reset)のパルスによってQはON状態を保持し、S(Set)のパルスによってQはOFF状態を保持します。
RとSの両方がONにした場合はQはOFFになるので、この回路はReset優先型のRSフリップフロップです。
Dラッチ(あと一息でDFF)
ここからだんだん複雑になってきます。
頭の中でのシミュレーションが大変になってきますが頑張ってください。
次はDラッチです。あと少しでDFFになる一歩手前の回路です。
先程のRSフリップフロップと見比べると、Rをnot Sに変換したあとに、それぞれに対する信号有効化のE(Enable)を追加したことが分かります。
EがONの状態のときにはCR1の状態はDの状態に一致します。
またEがOFF状態のときにはCR1の状態はOFFになる直前のCR1の状態を保持します。
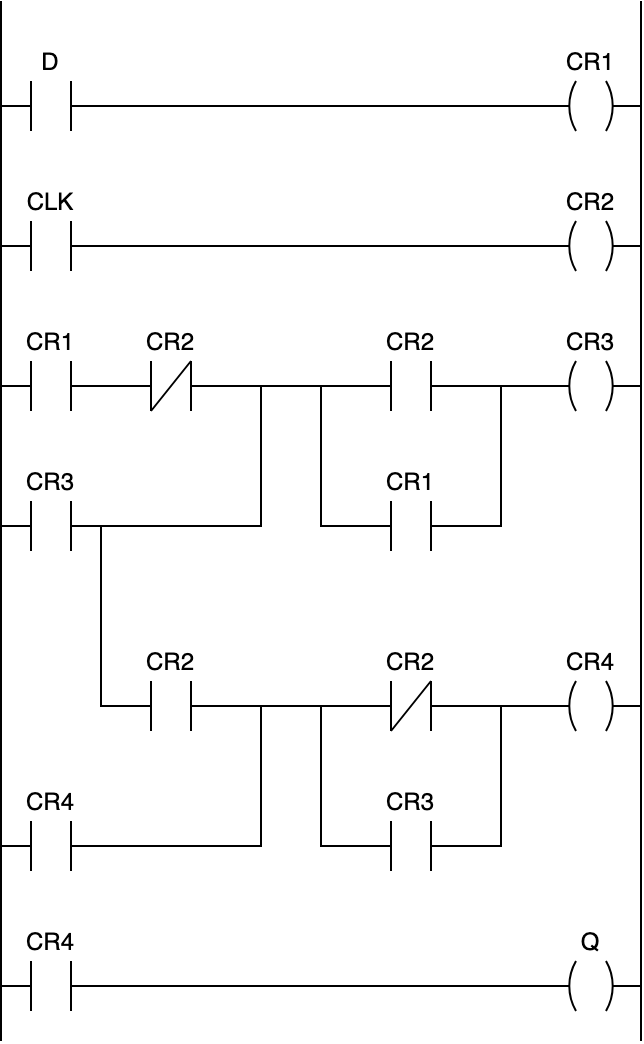
DFF(いよいよゴール)
ここまででDラッチまで完成しましたので、後はこれを2つ組み合わせることで目的のDFFになります。
いきなりラダー図で表現すると複雑なので、一旦もう少しだけ抽象度が高い図で表現します。
Dラッチをこのように組み合わせて作るDFFのことをマスター・スレーブ型DFFと呼びます。
入力側のDラッチをマスター、出力側のDラッチをスレーブと呼びます。
CLKがOFFからONになった瞬間(立ち上がり)のDの状態がQに保持されます。
CLKの立ち上がりのタイミングでMasterが保持していた状態がSlave側に転送され、その次の立ち上がりのタイミングまでは状態が変化することはありません。
そして、これをラダー図で実装します。上半分のブロックがMaster側で、下半分のブロックがSlave側です。
丁寧に順を追ってタイミングチャートを作ると、ちゃんとCLKの立ち上がりエッジでDの状態がCR2に取り込まれていることが分かります。
これでラダー図上ではDFFが完成しました。
最適化(実際に作ってみるための工夫)
上の節で概念的には完成したDFFを現実世界で実装してみます。
今回はこのリレーを使用してみます。
c接点が2つ入っています。
このリレーを使ってDFFを実装するにあたり、先程作ったラダー図では以下の問題があります。
- DとCLKの入力の個数が多いため、1つにまとめたい
というわけで、リレーを2つ追加してDとCLKの入力を1つにまとめます。
ついでに、出力も他回路につなげることを意識してバッファー付きにしておきます。
これで実装できるかと思いきや、また別の問題が出てきました。
- CR2とCR3の接点の個数が多すぎるので、これらを1つのリレーで実装できない
今回使用する946H-1C-5Dはc接点が2つあるだけなので、それに収まるようにします。
まずはCR2から最適化していきます。
並列に接続されている接点は上下入れ替えても等価なので入れ替えてます。
そして点線で囲んだ部分は1つのc接点で実現することができるので、CR2は1つのリレーで実装できます。
次にCR3を最適化していきます。
a接点が3つあるため、1つだけ減らせばOKです。
左にある2つのCR3のa接点が共通化できそうなので、共通化してみます。
この時、CR4のコイルに対する入力の条件は変更前と等価なことは自明ですが、CR3に対する入力の条件が本当に等価なのかは検証する必要があります。
CR3がONの場合は変更前後が等価なことは自明なので、CR3はOFFの時の振る舞いを考えます。
CR3の共通化によって赤線のパスが新たに作られます。
このパスを通ってCR3がONするためには、CR4がONかつCR2がONという条件が必要です。
一方で、この時にCR4のコイルに注目すると、CR2がONかつCR3がOFFという条件ではCR4は必ずOFFになることが分かります。
そのため、このパスによって変更前後の回路が等価ではなくなる状態は存在しないことが分かりましたので、安心してCR3の接点を共通化できました。
最終的には以下の回路になりました。
2c接点をもつリレーを4つ使うことでDFFが実現できます。
1c接点のコイルであれば、この倍の8つが必要です。
ブレッドボード上に実装してみました。
リレーは左から順にCR4, 3, 2, 1で、青タクトスイッチがCLK、黄色のタクトスイッチがDです。
遅延時間の測定(Analog Discoveryは高価だけど超有能)
せっかく作ったので、軽く性能測定を行います。
Analog Discovery 2を使ってCLKの立ち上がりがQに伝搬する遅延時間を測定してみます。
https://akizukidenshi.com/catalog/g/gM-10135/
QがOFF→ONになる時の遅延時間を測定してみます。
Qが立ち上がる瞬間にチャタリングが1ms発生していますが、最終的にON状態になっています。
チャタリングが完全に収まるまでの時間を遅延時間とすると、約11msという結果が得られました。
同様にON→OFFになる時の遅延時間も測定してみます。
こちらはチャタリングが発生していません。
また、遅延時間は約5msです。
なぜ、ON→OFFとOFF→ONの挙動に差があるのでしょうか?
リレーの接点がONになるときにはリレー内部の鉄片の運動エネルギーが有る状態からゼロの状態になる過程で何回かのバウンドが発生しているためだと考えられます。一方でOFFになるときには運動エネルギーがゼロの状態が初期状態であり、一旦接点が離れた後はバウンドすることなく鉄片はもう片方の接点に動くためにチャタリングが発生しないと考えられます。
また、このリレーのデータシートによると、Operate Time(OFF→ONの時間)とRelease Time(ON→OFFの時間)に数msの開きがあることが分かります。今回測定された遅延時間の差はこれによるものであると考えられます。

出典: https://akizukidenshi.com/download/ds/hsinda/941H-2C-5D.pdf
まとめ
論理ゲート作りで一番の難関ともいえるDFFを2c接点のコイル4つ(1cなら8つ)で実装することができました。