Go to Qiita Advent Calendar 2024 Top
LoginSignup
10
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

MIERUNEAdvent Calendar 2024

Day 20
@shiori0436inMIERUNE

Pythonで雪の結晶を描いてみよう（基本編）

Posted at

これは MIERUNE AdventCalendar 2024の20日目の記事です。
昨日は@Guarneri001さんによる「MapLibre GL JS + OpenCV」でした。

はじめに

皆さん、はじめまして。
今年も寒さが厳しい季節になり、MIERUNE本社がある北海道では、すっかり本格的な冬を迎えています。皆さんは、暖かくお過ごしでしょうか？

今年、初めてアドベントカレンダーに参加することとなり、この記事が記念すべき最初の投稿になります。その第一歩として、北海道の冬をテーマに「:snowflake:Pythonで雪の結晶を描いてみよう（基本編）:snowflake:」をお届けします。

本記事では、Pythonのライブラリを使ってシンプルな雪の結晶模様を描く方法をご紹介します。後日公開予定の「応用編」では、さらに複雑な模様作りに挑戦していく予定です。

雪の結晶の模様

雪の結晶は、雲の中で冷却された水蒸気が氷として成長し、六方向の対称性を有する特徴的な形を生み出します。

気温や湿度、風の影響を受けるため、同じ模様の結晶は一つとして存在せず、その組み合わせはまさに無限大です。
実際、雪の結晶にはプレート状、針状、樹枝状、星型など、多種多様なパターンがあります。

今回は、その中でも特に、「雪の結晶」と聞いて多くの人が思い浮かべる（であろう）、樹枝状のパターンをPythonで再現してみようと思います。

  • 今回、目指す形
    画像

事前準備

この記事では、Pythonを使って「雪の結晶の基本模様」を描画する方法をご紹介します。その前に、プログラムをスムーズに動かすための準備を整えておきましょう。以下の手順に沿って進めてみてください。

動作環境

筆者の環境は以下の通りです。お使いの環境に合わせて適宜調整してください。

  • OS: macOS
  • エディタ: Visual Studio Code
  • Pythonのバージョン: 3.12.2
  • ライブラリのバージョン: Matplotlib 3.9.2、NumPy 1.26.4

なお、macOSではフォントにHiragino Sansを使用していますが、Windows環境をご利用の場合は、以下のコードでフォントを設定することをおすすめします。

import matplotlib
matplotlib.rcParams['font.family'] = 'MS Gothic'  # Windowsの場合

インストール方法

Pythonの開発環境がすでに整っていることを前提に進めます。

もし、これから使用するライブラリがインストールされていない場合は、以下のコマンドをターミナルやコマンドプロンプトで実行してください。

pip install matplotlib numpy

ライブラリの紹介

今回使用するPythonライブラリをご紹介します。

1. Matplotlib

Matplotlibは、Pythonで最も広く使われているデータ可視化ライブラリの1つです。基本的には、折れ線グラフや棒グラフなどの描画やデータの可視化に使用しますが、今回のような幾何学的な図形の描画も簡単に行うことができます。

今回は主に、以下の機能を使用します：

  • pyplot ：図形や線を簡単に描画できるツール
  • subplots ：描画領域を作成するために使用
  • plot ：線や多角形を描画するために使用

公式ドキュメント： https://matplotlib.org/

2. NumPy

NumPyは、数値計算を効率的に行うためのライブラリで、Pythonの科学技術計算分野では欠かせない存在です。このライブラリを使うことで、数値データの操作や計算を効率的に行うことができます。

今回は主に、以下の機能を使用します：

  • np.linspace：指定した範囲を等間隔で分割した数列を生成
  • np.cos と np.sin：幾何学的な計算（例えば角度を用いた座標計算）で使用
  • np.pi：円周率（$π$）の値を取得するために使用

公式ドキュメント： https://numpy.org/ja/

補足として、NumPyの代わりにMathライブラリを使うことで同様の描画も可能です。

知っておきたい基本知識

六角形や対角線を描画するには、三角関数や座標の計算方法を少しだけ理解しておく必要があります。ここでは、必要な知識を簡単に説明します。

1. ラジアンって何？

ラジアンは、角度を表す単位です。Pythonで三角関数（cos や sin）を使うときには、角度をラジアンで指定する必要があります。

  • ラジアンと度数の対応関係：
    • 360度 = $2π$ ラジアン
    • 180度 = $π$ ラジアン
    • 90度 = $π/2$ ラジアン

例えば、六角形の頂点の角度は、360度を6等分した角度（60度間隔）に配置されます。これをラジアンに変換して、cos や sin に渡します。

2. 三角関数を使った座標計算

六角形の頂点や対角線の位置は、三角関数を使って計算します。

  • cos（コサイン）: 水平方向の位置（X座標）を計算
  • sin（サイン）: 垂直方向の位置（Y座標）を計算

計算の公式：

  • X座標： $x=center_x+size×cos(角度)$
  • Y座標： $y=center_y+size×sin(角度)$

3. 座標系の基本

六角形や対角線を描画する際には、中心座標と半径を基準に計算します。

  • 中心座標: 六角形の中心位置（例えば (0, 0)）。ここを基準に全ての頂点や線の位置を計算する
  • 半径（size）: 中心から頂点までの距離。この値を変えると六角形の大きさを調整できる

これで全ての準備が整いました！

次の章から、「雪の結晶の基本模様」の描画方法について解説していきます。

雪の結晶を再現してみよう！

ここからは、Pythonを使って「雪の結晶の基本模様」を再現していきます。全部で3つのステップに分けて進めていき、段階ごとに少しずつ完成形に近づけていきます。

最初の第一ステップでは、雪の結晶の基盤となる「六角形」を描画する方法をご紹介します。

画像

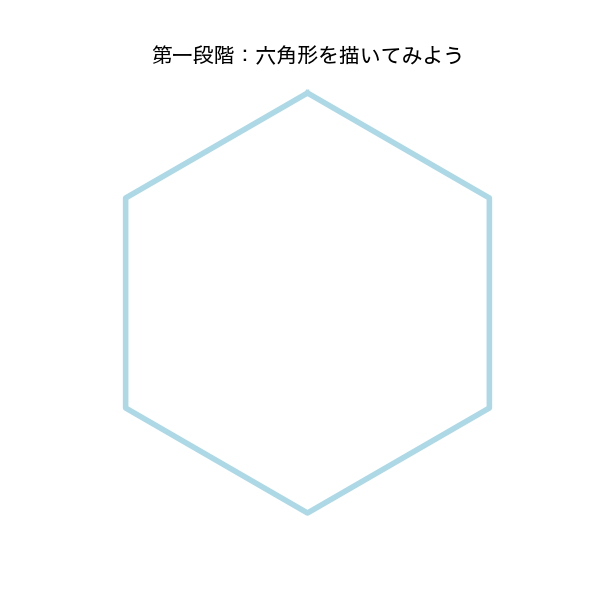
第一段階：六角形を描いてみよう

雪の結晶の形を作るための第一歩として、六角形を描画してみましょう。この六角形が雪の結晶の基盤となります。

コードの解説

以下は、六角形を描画するコードです。六角形の頂点を計算し、その頂点を結ぶことで六角形を描画します。

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# 日本語対応フォント設定
matplotlib.rcParams['font.family'] = 'Hiragino Sans'

def calculate_hexagon_points(center_x, center_y, size, num_sides=6):
    """六角形の頂点座標を計算"""
    return [
        # リスト内包表記
        (center_x + size * np.cos(angle), center_y + size * np.sin(angle))
        for angle in np.linspace(np.pi / 2, 2 * np.pi + np.pi / 2, num_sides + 1)[:-1]  # 初期角度をπ/2に
    ]

def draw_hexagon(ax, center_x, center_y, size, color='lightblue', linewidth=4):
    """六角形を描画"""
    points = calculate_hexagon_points(center_x, center_y, size)
    x, y = zip(*(points + [points[0]]))  # 六角形を閉じる
    ax.plot(x, y, color=color, linewidth=linewidth)

# 描画設定
fig, ax = plt.subplots(figsize=(6, 6))
ax.axis('equal')
ax.axis('off')
ax.set_title("第一段階：六角形を描いてみよう", fontsize=15)

# 1. 六角形を描画
draw_hexagon(ax, center_x=0, center_y=0, size=0.2)

plt.show()

主な処理の流れ

  1. 六角形の頂点を計算
    calculate_hexagon_points 関数では、六角形の各頂点の座標を計算をしています。

    def calculate_hexagon_points(center_x, center_y, size, num_sides=6):
    """六角形の頂点座標を計算"""
    return [
        # リスト内包表記
        (center_x + size * np.cos(angle), center_y + size * np.sin(angle))
        for angle in np.linspace(np.pi / 2, 2 * np.pi + np.pi / 2, num_sides + 1)[:-1]  # 初期角度をπ/2に
    ]
    • cosとsinを使い、それぞれのX座標とY座標を求めます。
    • ラジアンで表した角度を np.linspace を使って均等に分割し、360度を6等分（60度間隔）した座標を計算しています。
    • 初期角度を90度（$π/2$ ラジアン）に設定することで、六角形の頂点が上方向に来るよう調整しています。

  2. 六角形を描画
    draw_hexagon 関数では、calculate_hexagon_points 関数で算出した六角形の各頂点の座標をもとに、六角形を描画します。

    def draw_hexagon(ax, center_x, center_y, size, color='lightblue', linewidth=4):
    """六角形を描画"""
    points = calculate_hexagon_points(center_x, center_y, size)
    x, y = zip(*(points + [points[0]]))  # 六角形を閉じる
    ax.plot(x, y, color=color, linewidth=linewidth)
    • 六角形を閉じるために、最初の頂点をリストの最後に追加しています。

  3. 描画設定
    plt.subplots で描画領域の設定を行います。

    # 描画設定
fig, ax = plt.subplots(figsize=(6, 6))
ax.axis('equal')
ax.axis('off')
ax.set_title("第一段階：六角形を描いてみよう", fontsize=15)
    • ax.axis('equal')：描画領域を正方形に調整します。
    • ax.axis('off')：描画領域の軸を非表示にします。

実行結果

このコードを実行すると、以下のような六角形が描画されます。

画像

これで雪の結晶の基盤となる六角形を描画できました！
次の段階では、この六角形に対角線を加えて、さらに雪の結晶らしい形に進化させていきます。

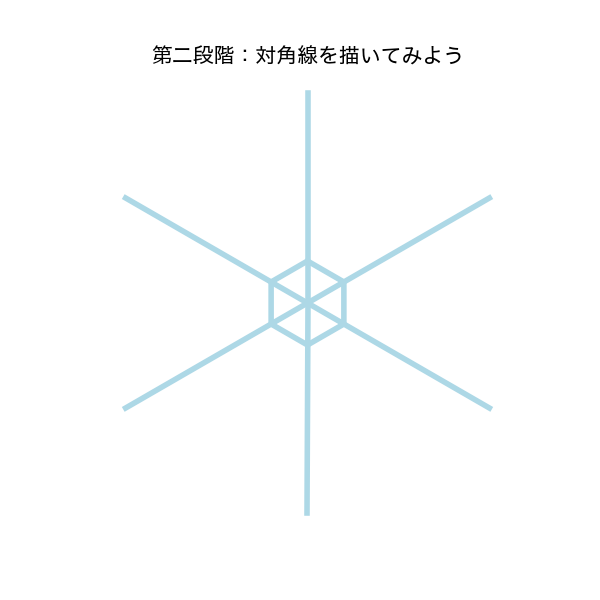
第二段階：対角線を描いてみよう

六角形を基に、中心から外周に伸びる対角線を描画してみましょう。この対角線を追加することで、六角形が雪の結晶らしい形に近づいていきます。

コードの解説

この段階では、前の段階で使用したdraw_hexagon関数に加え、新たに作成するdraw_diagonal_lines関数を使って、六角形に対角線を描画します。

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# 日本語対応フォント設定
matplotlib.rcParams['font.family'] = 'Hiragino Sans'

def calculate_hexagon_points(center_x, center_y, size, num_sides=6):
    """六角形の頂点座標を計算"""
    return [
        (center_x + size * np.cos(angle), center_y + size * np.sin(angle))
        for angle in np.linspace(np.pi / 2, 2 * np.pi + np.pi / 2, num_sides + 1)[:-1]
    ]

def draw_hexagon(ax, center_x, center_y, size, color='lightblue', linewidth=4):
    """六角形を描画"""
    points = calculate_hexagon_points(center_x, center_y, size)
    x, y = zip(*(points + [points[0]]))
    ax.plot(x, y, color=color, linewidth=linewidth)

def draw_diagonal_lines(ax, center_x, center_y, size, color='lightblue', linewidth=4):
    """対角線を描画"""
    angles = np.linspace(np.pi / 6, 2 * np.pi + np.pi / 6, 7)[:-1]
    for angle in angles:
        end_x = center_x + size * np.cos(angle)
        end_y = center_y + size * np.sin(angle)
        ax.plot([center_x, end_x], [center_y, end_y], color=color, linewidth=linewidth)

# 描画設定
fig, ax = plt.subplots(figsize=(6, 6))
ax.axis('equal')
ax.axis('off')
ax.set_title("第二段階：対角線を描いてみよう", fontsize=15)

# 1. 六角形を描画
draw_hexagon(ax, center_x=0, center_y=0, size=0.2)

# 2. 対角線を描画
draw_diagonal_lines(ax, center_x=0, center_y=0, size=1)

plt.show()

主な処理の流れ

  1. 対角線の角度を計算

    • np.linspace を使って、6本の対角線の角度を計算しています。

      # np.linspace(start, stop, num)
angles = np.linspace(np.pi / 6, 2 * np.pi + np.pi / 6, 7)[:-1]
      • 計算範囲:
        • start: 開始角度 $π/6$（30度）。
        • stop: 終了角度 $2π+π/6$（390度）。
      • 生成される角度:
        • ラジアン：[30度, 90度, 150度, 210度, 270度, 330度]
        • 最初の30度（$π/6$）は、六角形の中心を基点として、水平右方向（0度）から反時計回りに30度回転した位置から始まります。
      • 最後の角度を除外:
        • [:-1] で最後の角度（390度）を削除します。これは最初の角度（30度）と重複するからです。
      • なぜ30度から始めるのか？：
        • 六角形を縦軸が中央に来る形とするため、30度（$π/6$）を開始角度に設定しています。

  2. 対角線の描画

    for angle in angles:
    end_x = center_x + size * np.cos(angle)
    end_y = center_y + size * np.sin(angle)
    ax.plot([center_x, end_x], [center_y, end_y], color=color, linewidth=linewidth)
    • ループで各角度を処理:
      • angles に計算された6つの角度に対して、1本ずつ対角線を描画します。
    • 終点の座標を計算:
      • 各角度における対角線の終点（外周の座標）を三角関数を使って計算します。
        • X座標: $x=center_x+size×cos(角度)$
        • Y座標: $y=center_y+size×sin(角度)$

    対角線を描画:

    • ax.plot を使い、中心座標から外周の座標までの直線を描画します。
      • $角度=30°$の場合: 中心から右上の方向に線を描画。
      • $角度=90°$の場合: 中心から真上の方向に線を描画。

実行結果

このコードを実行すると、以下のように六角形とその中心から外周に向かう6本の対角線が描画されます。

画像

基本の六角形に対角線が加わり、雪の結晶らしい形が少しずつ見えてきましたね！
次の段階では、対角線上に小さな枝（V字）を描画して、「雪の結晶の基本模様」を仕上げていきます。

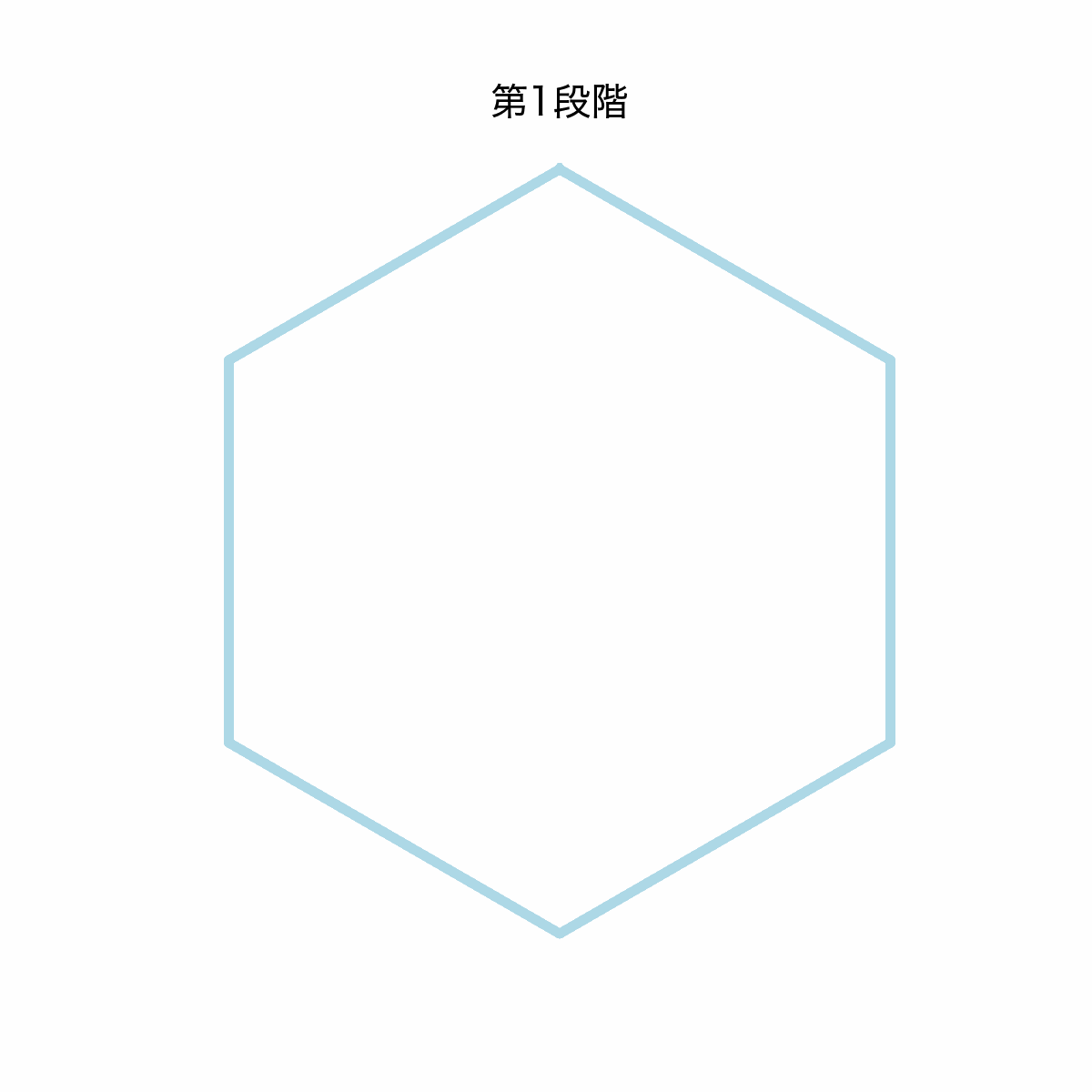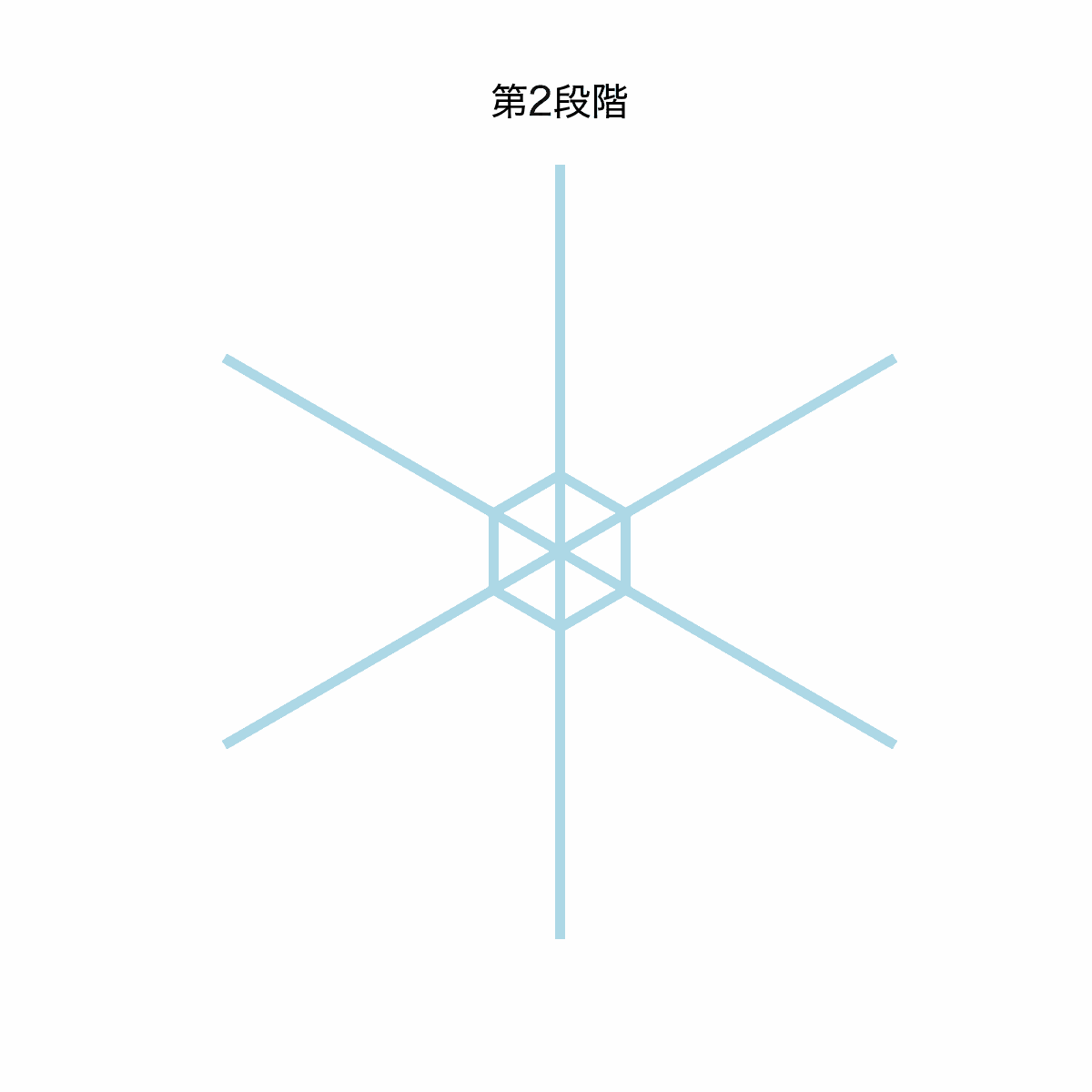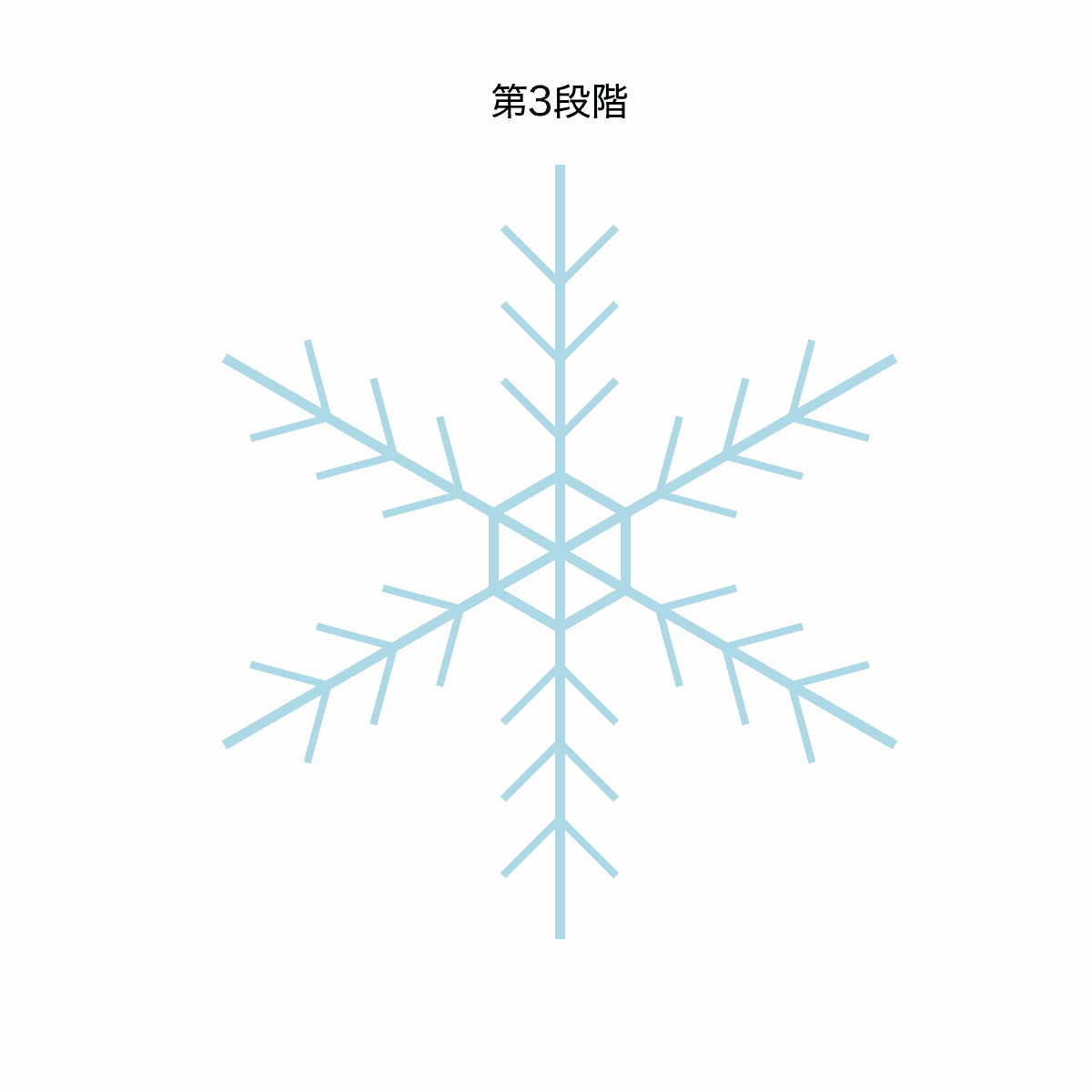
第三段階：V字の枝を描いてみよう

六角形と対角線が描けたら、いよいよ最後の仕上げです。
対角線上に小さなV字の枝を追加して、雪の結晶の基本模様を完成させましょう！

コードの解説

この段階では、前の段階で使用した draw_hexagon関数とdraw_diagonal_lines関数に加え、新たに作成するdraw_branches関数を使用して、対角線上にV字の枝を描画します。

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

# 日本語対応フォント設定
matplotlib.rcParams['font.family'] = 'Hiragino Sans'

def calculate_hexagon_points(center_x, center_y, size, num_sides=6):
    """六角形の頂点座標を計算"""
    return [
        (center_x + size * np.cos(angle), center_y + size * np.sin(angle))
        for angle in np.linspace(np.pi / 2, 2 * np.pi + np.pi / 2, num_sides + 1)[:-1]
    ]

def get_diagonal_angles():
    """対角線の角度を取得"""
    return np.linspace(np.pi / 6, 2 * np.pi + np.pi / 6, 7)[:-1]

def draw_hexagon(ax, center_x, center_y, size, color='lightblue', linewidth=4):
    """六角形を描画"""
    points = calculate_hexagon_points(center_x, center_y, size)
    x, y = zip(*(points + [points[0]]))
    ax.plot(x, y, color=color, linewidth=linewidth)

def draw_diagonal_lines(ax, center_x, center_y, size, color='lightblue', linewidth=4):
    """対角線を描画"""
    for angle in get_diagonal_angles():
        end_x = center_x + size * np.cos(angle)
        end_y = center_y + size * np.sin(angle)
        ax.plot([center_x, end_x], [center_y, end_y], color=color, linewidth=linewidth)

def draw_branches(ax, center_x, center_y, size, branch_length, num_branches, color='lightblue', linewidth=3):
    """対角線上にV字の枝を描画"""
    for angle in get_diagonal_angles():
        end_x = center_x + size * np.cos(angle)
        end_y = center_y + size * np.sin(angle)

        # 対角線上に配置
        for t in np.linspace(0.3, 0.7, num_branches):
            x_base = center_x + t * (end_x - center_x)
            y_base = center_y + t * (end_y - center_y)
            line_angle = angle  # 対角線の角度

            # V字の枝を描画
            for branch_angle in [np.pi / 4, -np.pi / 4]: # 45度左右
                x_branch = x_base + branch_length * np.cos(line_angle + branch_angle)
                y_branch = y_base + branch_length * np.sin(line_angle + branch_angle)
                ax.plot([x_base, x_branch], [y_base, y_branch], color=color, linewidth=linewidth)

# 描画設定
fig, ax = plt.subplots(figsize=(6, 6))
ax.axis('equal')
ax.axis('off')
ax.set_title("第三段階：V字の枝を描画してみよう", fontsize=15)

# 1. 六角形を描画
draw_hexagon(ax, center_x=0, center_y=0, size=0.2)

# 2. 対角線を描画
draw_diagonal_lines(ax, center_x=0, center_y=0, size=1)

# 3. V字の枝を描画
draw_branches(ax, center_x=0, center_y=0, size=1, branch_length=0.2, num_branches=3)

plt.show()

主な処理の流れ

  1. 対角線の終点を計算
    各対角線の終点（枝が描画される基準点）を計算します。

    # 六角形の中心が始点（center_x=0, center_y=0）になる
end_x = center_x + size * np.cos(angle)
end_y = center_y + size * np.sin(angle)
    • 対角線の角度（angle）を基に、三角関数（cos と sin）を使って終点座標を算出します。
    • 雪の結晶の「中心（center_x, center_y）」から「対角線の長さ（size）」までの位置を計算します。

  2. 対角線上に枝の基点を配置
    枝を描画する基点を対角線上に配置します。

    # num_branches回分、ループする
for t in np.linspace(0.3, 0.7, num_branches):
    x_base = center_x + t * (end_x - center_x)
    y_base = center_y + t * (end_y - center_y)
    • np.linspace(0.3, 0.7, num_branches) で、対角線上の枝の基点を配置する割合を指定。
      • 0.3: 中心から対角線の30%の位置。
      • 0.7: 中心から対角線の70%の位置。
      • num_branches: 枝の数（今回は3本）。
    • 基点の座標（x_base, y_base）を計算し、対角線上に等間隔で配置します。

  3. V字の枝を描画
    対角線上の基点からV字に枝を描画します。

    for branch_angle in [np.pi / 4, -np.pi / 4]:
    x_branch = x_base + branch_length * np.cos(line_angle + branch_angle)
    y_branch = y_base + branch_length * np.sin(line_angle + branch_angle)
    ax.plot([x_base, x_branch], [y_base, y_branch], color=color, linewidth=linewidth)
    • branch_angleを +45度（np.pi / 4）と-45度（-np.pi / 4）に設定。
    • 基点から左右に枝を伸ばす角度を指定。
    • branch_lengthを基に枝の長さを調整。
    • 各枝の終点（x_branch, y_branch）を計算し、基点（x_base, y_base）と結んで線を描画します。

実行結果

このコードを実行すると、六角形に対角線を追加し、その対角線上にV字の枝が描画されます。

画像

「:snowflake:雪の結晶の基本模様:snowflake:」の完成です!

おまけ

以下の機能を組み合わせることで、より動きのある魅力的な雪の結晶の描画が実現できます。

  • アニメーションをつけてみる。
  • 背景に雪を降らせてみる。
  • 背景色を変えてみる。

画像

GIF形式に変換すると、カラーバリエーションが256色に制限されるため、グラデーションの境目が目立ってしまいます。その点についてはどうかご容赦ください🙇‍♀️
実際の描画では、より滑らかで美しいグラデーションになりますので、参考としてPNG形式の画像も添付させていただきますね。

画像

まとめ

今回の記事では、Pythonを使って雪の結晶の基本模様を描画する方法を3つのステップに分けて解説しました。
数学的な知識を少し活用しながら、プログラミングで雪の結晶を再現する楽しさを感じていただけたでしょうか？
今回、描画ライブラリとして使用したMatplotlibには、本記事で紹介した内容以外にも、様々な機能が揃っています。これらの機能を活用して、ぜひ自分だけの雪の結晶を作成してみてください！

次回の応用編では、さらに複雑な雪の結晶模様を描画する方法をご紹介する予定です。

参考記事

明日は@bordorayさんによる記事です！お楽しみに！！

10
2
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
10
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?