はじめに
千葉県柏市に住む織姫と埼玉県越谷市に住む彦星は恋人同士です.
二人の間には江戸川が流れていますが, 橋は何本も架かっているので, 行き来にこれと言った不便はありません.
至って順調に見える二人の関係でしたが, ある日, 織姫は海外転勤を言い渡されてしまいました...
今日は七夕ということで, 遠距離恋愛を題材に, 「距離」というものについて再考したいと思います.
2点間の距離
2019年3月, 織姫は越谷, 彦星は柏で暮らしていました.
越谷 - 柏
まず, 越谷と柏の間の「距離」をGoogle Mapで調べてみました. ある地点で右クリックをすると"Measure Distance"と出てきます.
結果は「16.87 km」でした. これを経度と緯度から計算することを考えます.

Euclid距離
以後, 越谷と柏の座標は次の表で定めます. 経度は東, 緯度は北を正の方向とします.
| 都市名 | 経度 $\lambda$ | 緯度 $\phi$ |
|---|---|---|
| 越谷 | 139.970779 | 35.862065 |
| 柏 | 139.786040 | 35.888076 |
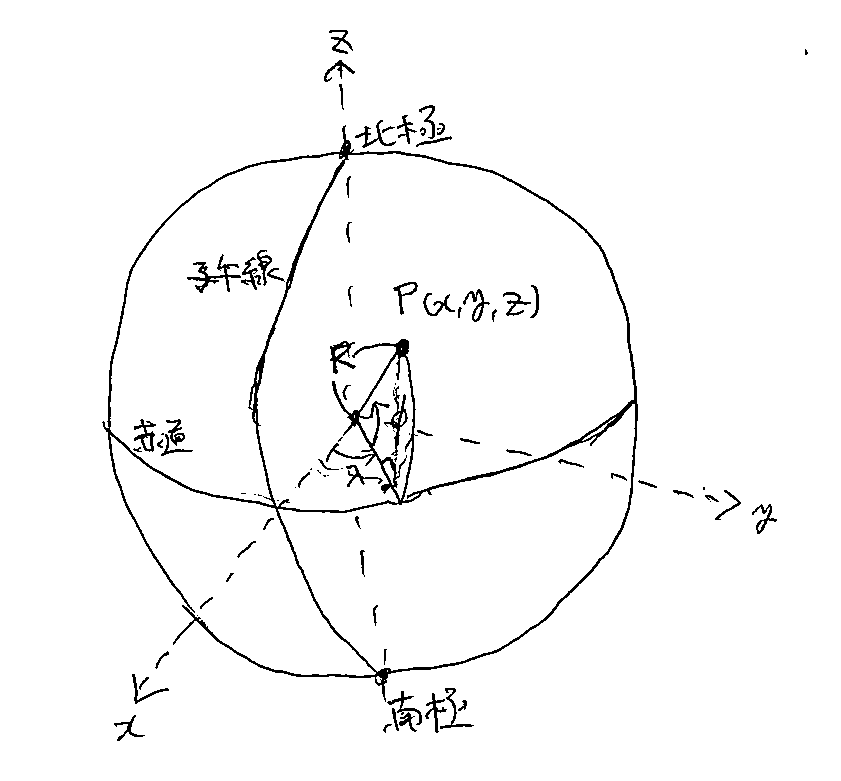
この座標は球面座標表示になっているので, 地球の半径を$R=6378.1 \mathrm{km}$として, 次のように直交座標に変換します(手書きの図で失礼します).
\begin{align}
x &= R\cos{\phi}\cos{\lambda}\\
y &= R\cos{\phi}\sin{\lambda}\\
z &= R\sin{\phi}
\end{align}
$p_1=(x_1,y_1,z_1)$と$p_2=(x_2,y_2,z_2)$のEuclid距離は次の式で定めます.
$$
D_{Euc}(p_1, p_2) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2}
$$
Pythonだと次のように書けます.
def euclidize(degs):
lamda, phi = np.radians(degs)
x = R * np.cos(phi) * np.cos(lamda)
y = R * np.cos(phi) * np.sin(lamda)
z = R * np.sin(phi)
return np.array([x,y,z])
def euclidian_dist(pol1, pol2):
euc1 = euclidize(pol1)
euc2 = euclidize(pol2)
diff = euc1 - euc2
return np.sqrt(np.dot(diff, diff))
ori = [139.970779, 35.862065]
hiko = [139.786040, 35.888076]
euclidian_dist(ori, hiko)
# >> 16913.382975766835
結果は16.91kmでした.
測地線距離
越谷を点A, 柏を点B, 地球の中心を点Oとすると, 先ほど求めたEuclid距離は線分ABと対応します. しかし, このように地球を貫く経路は現実的でないので, 実際には弧ABの長さを求めたいです.

$\angle \mathrm{AOB} = \theta$とすると, 球面上での測地線距離は次の式で定められます.
$$
D_{geo}(R, \theta) = R\theta
$$
Pythonで計算します.
def geodesic_dist(pol1, pol2):
d_euc = euclidian_dist(pol1, pol2)
theta = 2 * np.arcsin(d_euc/2/R)
return R * theta
geodesic_dist(ori, hiko)
# >>16913.387931385758
結果は変わらず「16.91km」でした(少しだけ大きくなりました). 今回は$\theta$が小さかったので, 弧ABは線分ABでよく近似できたということですね.
Manhattan距離
Google Mapで2地点間の「道のり」を測ると「20.9km」でした.
このような距離の測り方に対応するものとして**Manhattan距離 (市街地距離)**があります. Manhattanのような通りが格子状に走っている街で2地点間の「道のり」を表す距離で, 次の式で定められます. 詳しくは[3]をご覧ください.
$$
D_{Man}(p_1, p_2) = |x_1-x_2| + |y_1-y_2| + |z_1-z_2|
$$
Euclid距離のときに定めた直交座標系に沿って格子状の道が走っていると仮定した場合の越谷 - 柏間のManhattan距離は次のように計算されます(地球サイズのクレーンゲームで越谷から柏にクレーンを移動させるときの軌跡の長さを想像してください).
def manhattan_dist(pol1, pol2):
euc1 = euclidize(pol1)
euc2 = euclidize(pol2)
diff = euc1 - euc2
return np.sum([np.abs(d) for d in diff])
manhattan_dist(ori, hiko)
# >>26030.942586314864
結果は「26.03km」でした.
Chebyshev距離
座標の各成分の差分の絶対値の最大値をChebyshev距離と呼び, 次の式で定義されます.
$$
D_{Cheb}(p_1, p_2) = \max{ (|x_1-x_2|, |y_1-y_2| ,|z_1-z_2|) }
$$
Pythonでは次のように計算されます.
def chebychev_dist(pol1, pol2):
euc1 = euclidize(pol1)
euc2 = euclidize(pol2)
diff = euc1 - euc2
return np.max([np.abs(d) for d in diff])
chebychev_dist(ori, hiko)
# >>12035.805316988379
結果は「12.03km」でした.
Minkowski距離
ここまでに紹介したEuclid距離, Manhattan距離, Chebyshev距離は, すべてMinkowski距離 (Lp距離) の特別な場合と考えることができます.
Minkowski距離は次で定められます.
$$
D_{Min}(p_1, p_2) = \Bigl(\sum_{i}|p_{1i}-p_{2i}|^p\Bigr)^{1/p}
$$
$p=1,2,\infty$の場合にそれぞれManhattan距離, Euclid距離, Chebyshev距離となります. 詳しくは[4]をご覧ください.
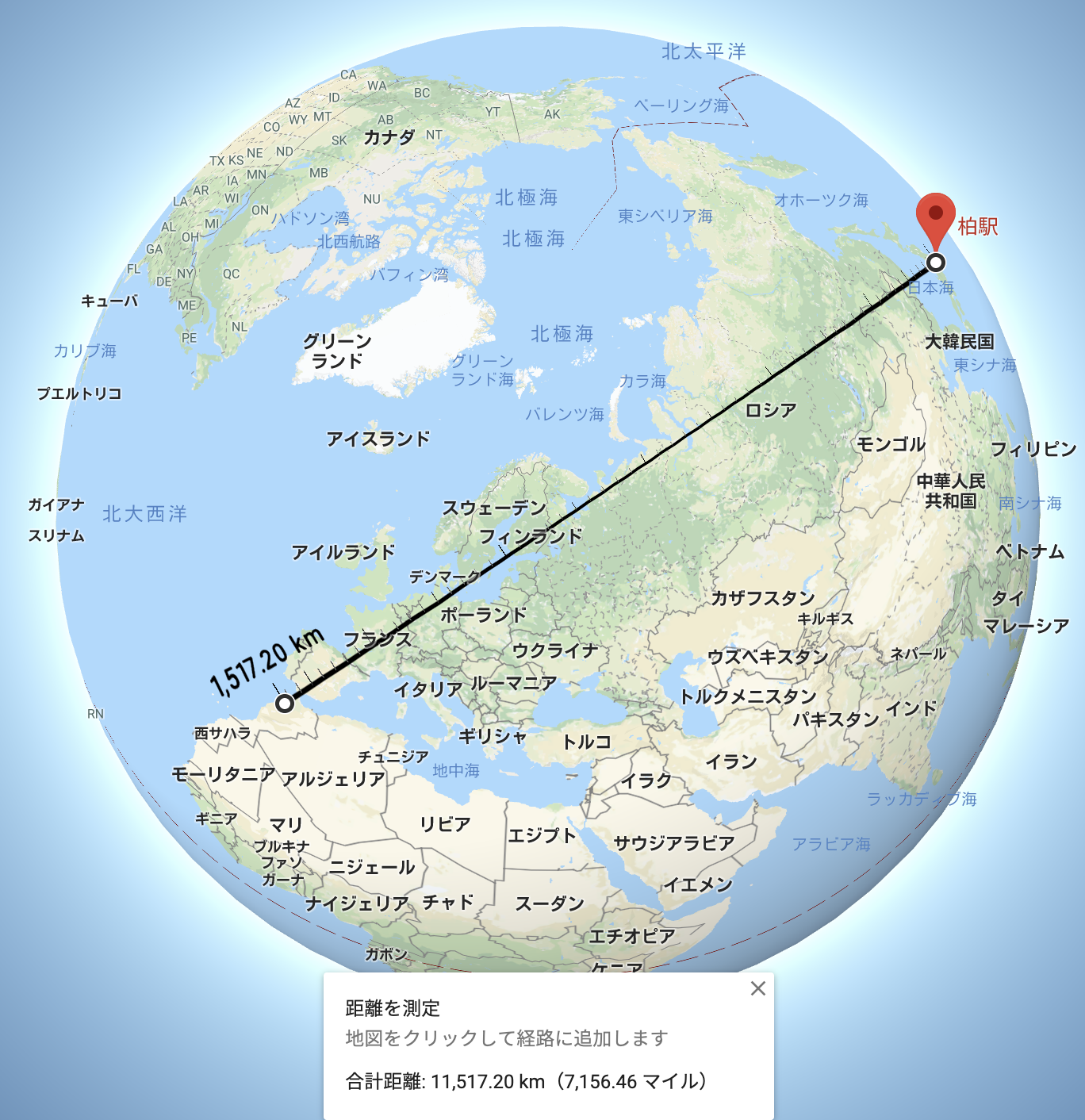
ラバト - 柏
2019年4月, 織姫はモロッコのラバトにあるオフィスに転勤することになりました.
遠距離恋愛の始まりです. 2人の距離はどのくらいになるでしょうか?
| 都市名 | 経度 $\lambda$ | 緯度 $\phi$ |
|---|---|---|
| ラバト | -6.855500 | 34.002235 |
| 柏 | 139.786040 | 35.888076 |
前節で定義した関数で計算した結果をまとめて示します.
| 距離関数 | 距離[km] |
|---|---|
| 測地線 | 11519.65 |
| Manhattan ($p=1$) | 13335.16 |
| Euclid ($p=2$) | 10016.52 |
| Chebyshev ($p=\infty$) | 9195.70 |
同じ座標でも, Lpノルムの$p$の値を大きくすると距離は小さくなることが確認できます.
Chebyshev距離で考えれば2人の距離が小さくなるということです!
確率分布間の距離
少し見方を変えて, 二人がそれぞれ点ではなく確率分布であると考えてみましょう.
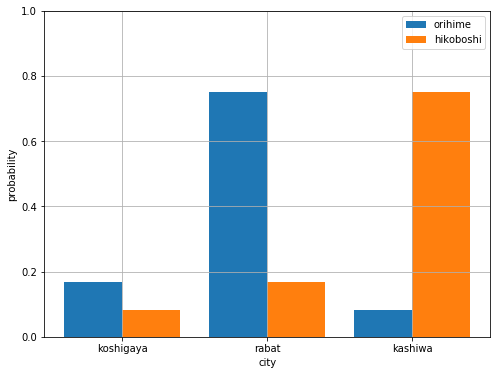
12ヶ月のうち, 織姫は2ヶ月を越谷, 9ヶ月をラバト, 1ヶ月を柏で過ごし, 彦星は1ヶ月を越谷, 2ヶ月をラバト, 9ヶ月を柏で過ごすとして, 電子雲のように各地点において分布として存在するイメージです. 確率分布をヒストグラムで表すと次のようになります.
# [koshigaya, rabat, kashiwa]
ori = np.array([2, 9, 1])/12
hiko = np.array([1, 2, 9])/12
plt.figure(figsize=(8,6))
plt.bar([1,2,3], ori, width=0.4, label='orihime')
plt.bar([1.4,2.4,3.4], hiko, width=0.4, label='hikoboshi')
plt.xticks([1.2, 2.2, 3.2], ['koshigaya', 'rabat', 'kashiwa'])
plt.xlabel('city')
plt.ylabel('probability')
plt.legend()
plt.ylim([0,1])
plt.grid()
plt.show()
Kullback–Leibler距離
確率分布間の距離を測るための関数として最も有名なのはKullback–Leibler距離 (KLダイバージェンス; KL情報量; 相対エントロピー) でしょうか. 位置を表す確率変数を$X$として, 織姫と彦星の分布関数をそれぞれ$p(x), q(x)$とすると, $p$と$q$のKL距離は次で定められます.
$$
D_{KL}(p||q) = \int_{-\infty}^{\infty}p(x)\log{\frac{p(x)}{q(x)}}dx
$$
これは$p$と$q$の情報量の差の$p$に関する期待値を取ったもので, 確率値の配列を引数にとる関数として簡単に書けます.
def kl_dist(p, q):
return sum(p * np.log(p/q))
ただし, KL距離は式の形を見て分かる通り, $p$と$q$に関して非対称です. 実際に計算すると,
print('ori-hiko:', kl_dist(ori, hiko))
# >>ori-hiko: 1.06048052956
print('hiko-ori:', kl_dist(hiko, ori))
# >>hiko-ori: 1.33947660183
となります. KL距離は距離の公理 :
- $D(x,y)\geq0$ (非負性)
- $D(x,y)=0 \iff x=y$ (同一律)
- $D(x,y) = D(y,x)$ (対称律)
- $D(x,z)\leq D(x,y)+D(y,z)$ (三角不等式)
のうち対称律と三角不等式を満たさないため, 厳密には距離関数ではありません(そのため「ダイバージェンス」と呼ばれます).
Jensen-Shannon距離
KL距離の非対称性を克服したものとしてJensen-Shannon距離 (JSダイバージェンス) が提案されています.
\begin{eqnarray}
m(x) &=& \frac{p(x)+q(x)}{2}\\
D_{JS}(p||q) &=& \frac{D_{KL}(p||m) + D_{KL}(q||m)}{2}
\end{eqnarray}
こちらも簡単に実装できます. 対称性も確認しましょう.
def js_dist(p, q):
m = (p+q)/2
return (kl_dist(p,m)+kl_dist(q,m))/2
print('ori-hiko:', js_dist(ori, hiko))
# >>ori-hiko: 0.260817818792
print('hiko-ori:', js_dist(hiko, ori))
# >>hiko-ori: 0.260817818792
JS距離も三角不等式を満たさないため, 厳密には距離関数ではありません.
Wasserstein距離
KL距離の定義式を見てみると, $\log{\frac{p(x)}{q(x)}}$に$q(x)=0$になるような$x$があればゼロ除算になってしまいますし, $p(x)=0$になるような$x$があれば$\log0$となってしまうことがわかりますが, これは計算を非常に不安定にします.
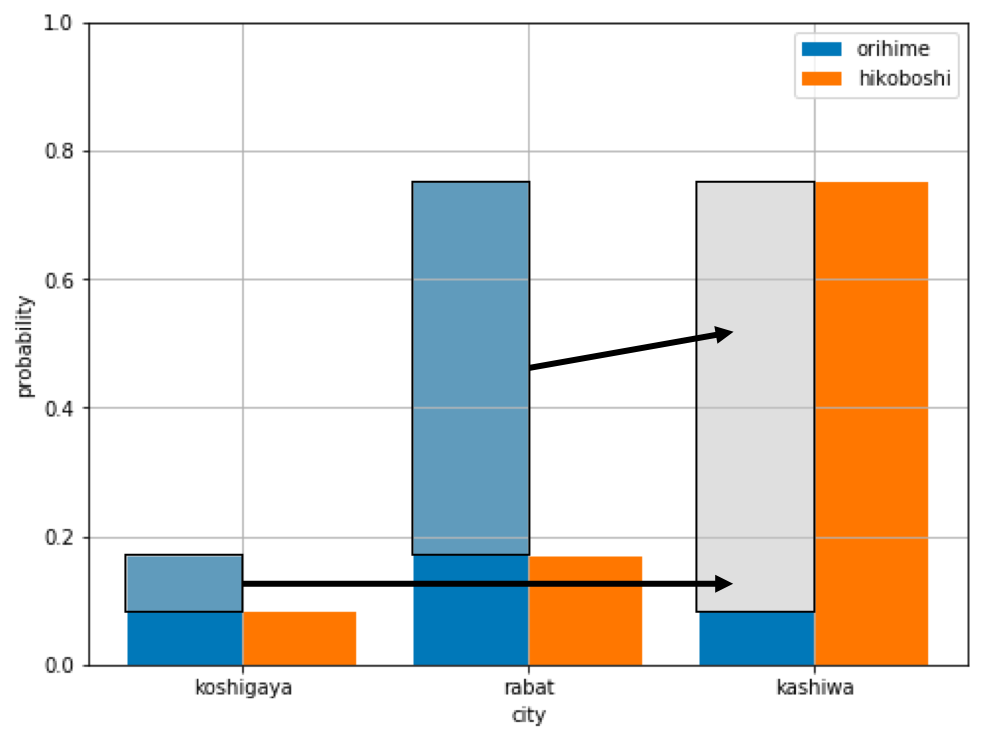
このような観点からより安定性の高い距離関数として, Wasserstein距離 があります. W距離は直感的には, 確率分布を砂山だとみなし, 砂山$p$を別の砂山$q$に変形させるときにかかる最小コスト(質量×距離)です. earth mover's distance (EMD) とも呼ばれます.
W距離は, $p(x)$と$q(x)$のすべての可能な同時分布を$\Pi(p,q)$として, その中での輸送距離の期待値の下限として定められます.
$$
D_W(p, q) = \inf_{\gamma \sim \Pi(p, q)} \int_{(x, y) \sim \gamma}D(x,y)dxdy
$$
$D(x,y)$は2点間の距離を定めるLipschitz連続な関数で, ここでは測地線距離とします.
これを実装するには最小化問題を解かなければならないため少し厄介です. SciPyにはW距離が実装されているようですが, 球面上で使うのは大変そうだったので, ここはアドホックに解くことにします.
図のように, 越谷とラバトから織姫の余分な砂を柏に持っていけば, 最小コストで彦星と同じ砂山ができます.
koshigaya = [139.970779, 35.862065]
kashiwa = [139.786040, 35.888076]
rabat = [-6.855500,34.002235]
earth_koshigaya = ori[0]-hiko[0]
earth_rabat = ori[1]-hiko[1]
w_dist = earth_koshigaya*geodesic_dist(koshigaya, kashiwa) + earth_rabat*geodesic_dist(rabat, kashiwa)
print(w_dist)
# >>6721207.71245
W距離は単位をmとしてもよいでしょう. ということで, 結果は「6721.21km」でした.
測地線距離の平均
もっと素朴なアプローチとして, 2人を動点として2点間の測地線距離の時刻に関する平均をとることもできます.
先程示した確率分布を満たしながら2人がなるべく近くにいられるようにすると, 例えば4月から3月まで
ori = [koshigaya, rabat, rabat, rabat, rabat, rabat, rabat, rabat, koshigaya, kashiwa, rabat, rabat]
hiko = [koshigaya, kashiwa, kashiwa, rabat, rabat, kashiwa, kashiwa, kashiwa, kashiwa, kashiwa, kashiwa, kashiwa]
のように動くことができます. このとき, 測地線距離の平均は,
np.mean([geodesic_dist(o,h) for o,h in zip(ori, hiko)])
# >>6721207.7124540322
結果はW距離と等しい「6721.21km」になりました.
2人の動き方次第でこの値は変わりますが, W距離はこの「測地線距離の時間平均」の最小値を与えています.
確率分布間の距離には他にもL2距離やPearson距離などがあるようですが, 単位をmにできるものは私の知る限りこのくらいです.
おわりに
様々な距離関数を考えることで, 織姫と彦星の距離を「11519.65km」から「6721.21km」まで減らすことができました. ひとくちに「遠距離恋愛」といっても, いろいろな距離がありますね.
| 距離関数 | 距離[km] |
|---|---|
| 測地線 | 11519.65 |
| Manhattan ($p=1$) | 13335.16 |
| Euclid ($p=2$) | 10016.52 |
| Chebyshev ($p=\infty$) | 9195.70 |
| Wasserstein | 6721.21 |
七夕なので短冊を飾って本記事の結びとします. 高い目標ではありますが, 精進を続けて参ります…!
ーーーーーー | 数 | | 学 | | を と | | 完 コ | | 全 ン | | に ピ | | 理 ュ | | 解 | | | で タ | | き | | | ま サ | | す イ | | よ エ | | う ン | | に ス | ーーーーーー参考文献
[1] 【Day-23】機械学習で使う"距離"や"空間"をまとめてみた - プロクラシスト
いろいろな距離をまとめた表があり, 参考にさせていただきました.
[2] 杉山将, "確率分布間の距離推定 : 機械学習分野における最新動向", 日本応用数理学会論文誌, 2013.
[3] マンハッタン距離 - Wikipedia
Manhattan距離は通りが直交するManhattanでの移動距離にちなんで名付けられたそうです.
[4] ノルムの意味とL1,L2,L∞ノルム | 高校数学の美しい物語
単位円の図がわかりやすいです.
[5] Lilian Weng, "From GAN to WGAN", 2017.
GANの文脈でKL距離, JS距離, W距離の違いを解説したブログで, 非常にわかりやすかったです.
[6] 小林昭七, "曲線と曲面の微分幾何", 裳華房, 1995.
球面上でW距離などを考えるのに役立ちそうですが, そこまでたどり着けませんでした. どなたか続きをお願いします笑
[7] データサイエンス概論第一=2-1 データ間の距離と類似度
「2点間の距離」を丁寧に説明したスライドです. Minkowski距離で$p=\infty$とするとChebyshev距離になることなども説明されています.