はじめに
錯視(目の錯覚)はいろいろなところで見かけますよね.
例えば, エッシャーの『上昇と下降』(ペンローズの階段)はみなさんご存知かと思います.
今回は, この「無限に続く階段」を聴覚情報, すなわち音で再現してみます.
この「無限に高く(低く)なっていく音」は1964年にベル研究所のRoger N. Shepardが考案した「1オクターブ上がっても最初と同じに聞こえる音」を発展させたもので, 「シェパードトーン(無限音階)」と呼ばれています.
まずは完成した音を聞いてみてください.
Audio illusion: Shepard tone (upward) - YouTube
Audio illusion: Shepard tone (downward) - YouTube
おもしろいですよね?
ちなみに, シェパードトーンは映画や音楽でもときどき登場します.
特にChristopher Nolan監督はシェパードトーンが大のお気に入りだそうで, 2017年公開の映画Dunkirkでの使用例がこちらの動画で詳しく解説されています.
The sound illusion that makes Dunkirk so intense
言われてみれば, Inceptionでも使われていたような…
音楽界ではPink FloydのEchoesなどがあります.
2018年にリリースされたFranz FerdinandのAlways Ascendingでは, 「The Shepard misleads so you think you're transcending」と歌われています.
原理
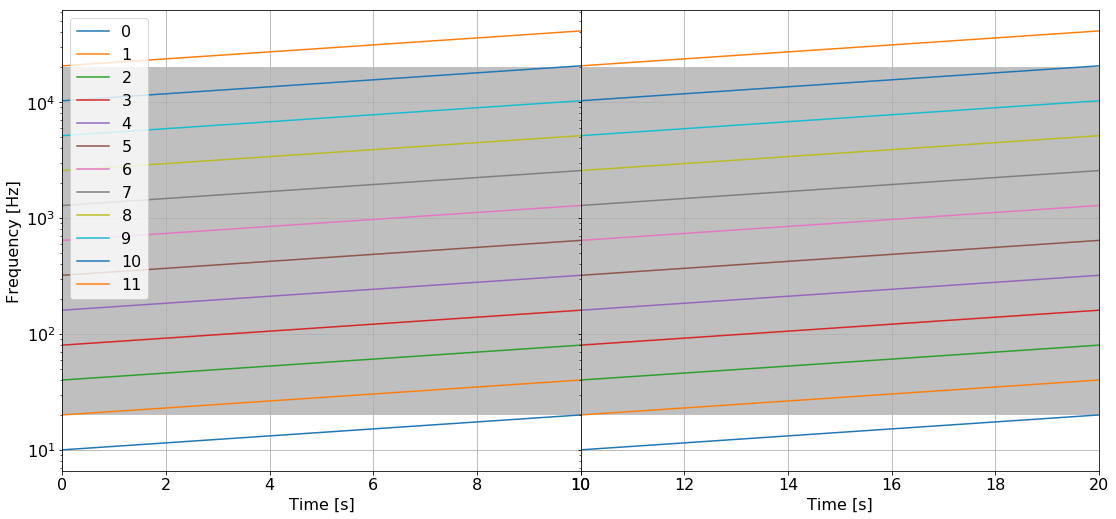
音源は10秒で1サイクルとします.
図のように, 1オクターブずつ離れたいくつかの音を10秒間かけて連続的に1オクターブ高くします.
グレーの領域は可聴域(約20Hz-20kHz)です.
*周波数が2倍になると音の高さは1オクターブ上がります. グラフの縦軸が対数スケールなのはそのためです.
1サイクルの中で1オクターブ上昇するこの音を周期的に繰り返すと, 境界のところがうまく繋がって, 無限に高くなっているように聞こえるという仕組みです.
ただし, 位相は揃えていないので, 耳がとてもいい人は気づくかもしれません.
床屋のアレみたいですね.
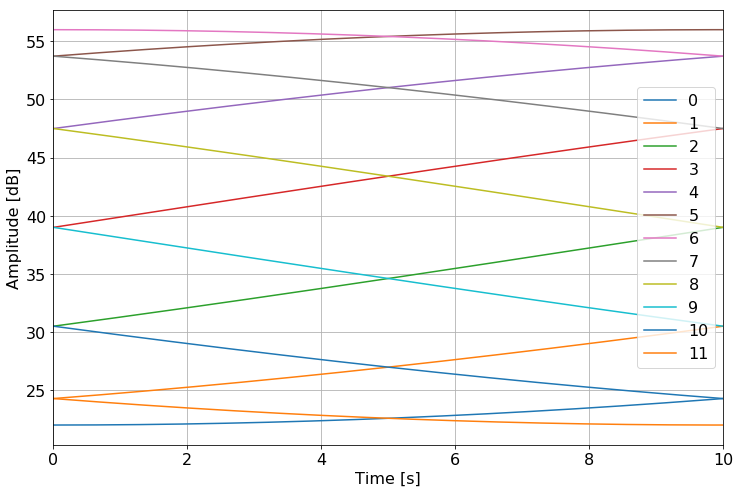
可聴域の境界付近では音圧レベルを小さくして, 図のように滑らかにフェードイン/アウトさせています.
2つのグラフを見比べてみましょう.
0番目の波は, 10Hzから20Hzに上がるにつれて20dBから24dBまで上昇しています.
11番目の波は, 20kHzから40kHzに上がるにつれて24dBから20dBまで下降しています.
これを式で表すとどうなるでしょうか.
$c_{max}$個の波を重ね合わせるとして, $c$番目の波の時刻$t$における周波数$f$と振幅$A$を次のように定義します.
\begin{eqnarray}
f(t, c) &=& f_{min}\, 2^{c+\frac{t}{t_{max}}}\\
A(y, c) &=& 10^{\frac{L(t,c)}{20}}
\end{eqnarray}
上式で出てきた音圧レベル$L(t, c)$は次の式で定義されます.
\begin{eqnarray}
L(t, c) &=& L_{min} + (L_{max}-L_{min})\,\frac{1-\cos{\theta(t,c)}}{2}\\
\theta(t, c) &=& \frac{2\pi}{c_{max}}\Bigl( c+\frac{t}{t_{max}} \Bigr)
\end{eqnarray}
周波数$f$を時間積分して位相とし, sin波の中に入れて振幅$A$をかけると1つの波ができます.
w_{c}(t) = A(t, c)\sin{\Bigl( 2\pi\int_0^t f(\tau, c) d\tau \Bigr)}
これを$c_{max}$個だけ重ね合わせると, グラフのような音の特性が実現できます.
w(t) = \sum_{c=0}^{c_{max}-1} w_{c}(t)
実装
サンプルレートを44100Hzとして, wavファイルに保存しました.
大抵の場合は$f_{min}=10, c_{max}=12$でうまくいくと思います.
import numpy as np
from scipy.io import wavfile
spl = 44100
secs = 10
tmax = spl*secs
Lmin = 22
Lmax = 56
cmax = 12
fmin = 10
def shift(t, c):
return c + t/(tmax)
def theta(t, c):
return 2*np.pi/cmax*shift(t, c)
def L(t,c):
return Lmin + (Lmax-Lmin)*(1-np.cos(theta(t, c)))/2
def fr(t, c):
return fmin*2**shift(t, c)
def amp(t, c):
return 10**(L(t, c)/20)
def main():
parser = argparse.ArgumentParser(description='Shepard tone')
parser.add_argument('--down', '-d', type=bool, default=False, help='Set True for going down')
args = parser.parse_args()
t = np.linspace(0, tmax-1, tmax)
wave = np.zeros(tmax)
for c in range(cmax):
# 周波数は時間積分して位相とする
wave += amp(t, c)*np.sin(2*np.pi*np.cumsum(fr(t, c))/spl)
wave = np.hstack((wave, wave))
if args.down:
wave = wave[::-1]
wave = (wave/np.max(wave)).astype(np.float32)
if args.down:
wavfile.write("shepard_down.wav", spl, wave)
else:
wavfile.write("shepard_up.wav", spl, wave)
if __name__ == '__main__':
main()
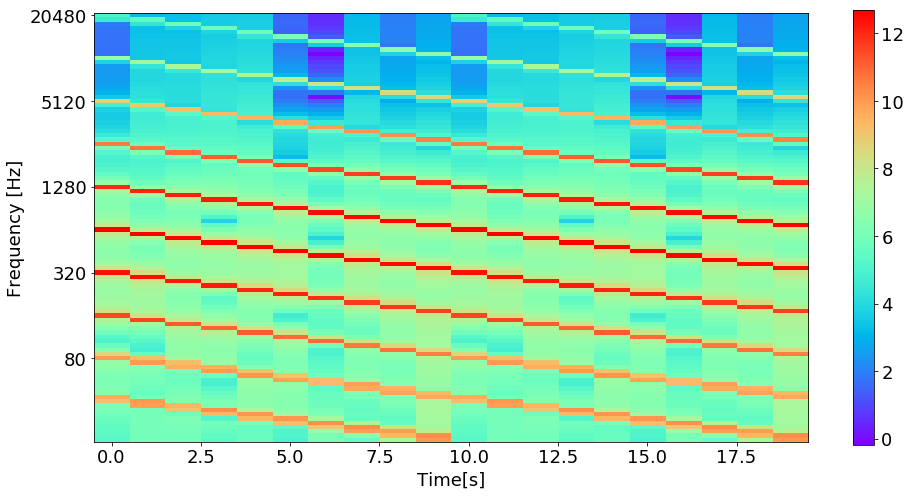
これを逆に再生すれば, 下がっていく音を実現できます.
解析
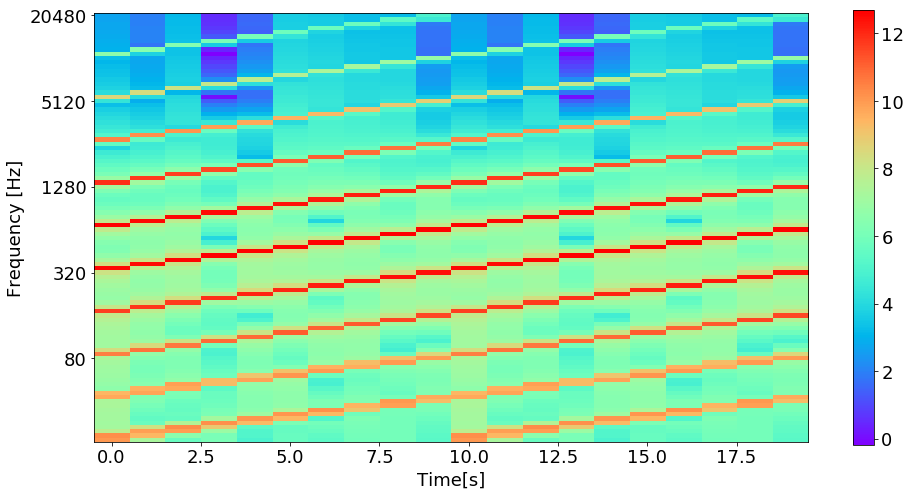
最後に, matplotlibとnumpyでスペクトログラムを描いてみましょう!
スペクトログラムとは, 横軸に時間, 縦軸に周波数(対数)を取り, 色でその強度(対数)を示したヒートマップです.
ナイキスト周波数が22050Hzで, これ以上の周波数成分が含まれているとフーリエ変換するときにエイリアシングを起こしてしまいます.
そのため, 解析のときは$f_{min}=20, c_{max}=10$としてナイキスト周波数以下に収まるようにしました.
N = 2*secs
ham = np.hamming(spl) # ハミング窓
# 窓の幅*秒数の行列にしてFFTを1度で行う
ham = np.tile(ham, (N,1))
sig = wave.reshape(( N, spl))*ham
spec = np.fft.fft(sig.T, axis=0)
spec = np.abs(spec)**2 # パワースペクトル
y_idx = np.logspace(np.log10(20), np.log10(20480), 100).astype("int32") # 対数軸にするときに使うインデックス
log_spec = np.log10(spec)
plt.figure(figsize=(16,8))
plt.rcParams["font.size"]=18
plt.imshow(np.flipud(log_spec[y_idx, :]), cmap='rainbow', aspect=0.12)
plt.colorbar()
ax = plt.gca()
plt.xlabel("Time[s]")
plt.ylabel("Frequency [Hz]")
ax.set_yticklabels([0, 20480, 5120, 1280, 320, 80, 20,])
plt.show()
このような図が得られます. 数式との対応がイメージできるでしょうか.
下がっていくときの図はこちらです.
参考文献
[1] R. N. Shepard, "Circularity in Judgments of Relative Pitch", The Journal of Acoustical Society of America, Vol. 36, No. 12, pp. 2346-2353, 1964.
元となった論文です.
[2] 無限に上がり続ける音~無限音階
[1]を元に無限音階を作った方の解説記事です.
[3] Shepard tone - Wikipedia
使用例が詳しいです.