勾配法実装1

はじめに

アドベントカレンダーのこの日を予約してから早1ヶ月程が経ち、クリスマス目前となりました。なんだか、いつも以上に今年1年間はあっというまに過ぎ去った気がします。今回は、ある程度Pythonは書けるけど、機械学習で具体的にどんな実装をするのか知らない人向けに、僕からのクリスマスプレゼントとして、なるべくわかりやすくまとめてこれをお送りします。理論的な部分と実践的な部分が混じっているのでわかりそうなところだけつまみ食いしてみてください。多分それでも雰囲気はつかめると思います。前回の記事で機械学習の直観的な描像はまとめてあるのでこちらも参考にしてください。

勾配法とは

勾配法とは、最適化に用いられる方法の1つです。最適な出力を与える重み$W$を求めるためにしばしばこの勾配法が用いられます。

具体的には前回示した2乗和誤差

$$ \frac{1}{N} \sum_{n=1}^{N}||\boldsymbol{y}_{n}(\boldsymbol{x}_{n},W)-\boldsymbol{t}_{n} ||^{2} \tag{1}$$

を最小にする方法の一つが勾配法であり、微分を用いて最小値を求めます。

微分の実装

まず手始めに1次元の微分を実装しましょう。
$x$ の関数 $f(x)$ の微分 $f^{\prime}(x)$ は
$$ f^{\prime}(x) = \lim_{h → 0} \frac{f(x + h) - f(x)}{h} \tag{2}$$で定義されます。微分は点 $x$ における関数 $f(x)$ の傾きを意味します。
例えば関数が $f(x) = x^2$ のとき
$$ f^{\prime}(x) = \lim_{h → 0} \frac{(x + h)^2 - x^2}{h} = 2x \tag{3}$$となります。
実装は例えば以下のようになります。(主要なimport先は下のコードだけ書いておくので以降も基本的には忘れないようにしてください。)

numerical_differentiation.py

import numpy as np
import matplotlib.pylab as plt

def nu_dif(f, x):
    h = 1e-4
    return (f(x + h) - f(x))/(h)

def f(x):
    return x ** 2

x = np.arange(0.0, 20.0, 0.1)
y = nu_dif(f, x)

plt.xlabel("x")
plt.ylabel("y")
plt.plot(x,y)
plt.show() 

これで下のグラフ $y=f^{\prime}(x)=2x$ がプロットされるはずです。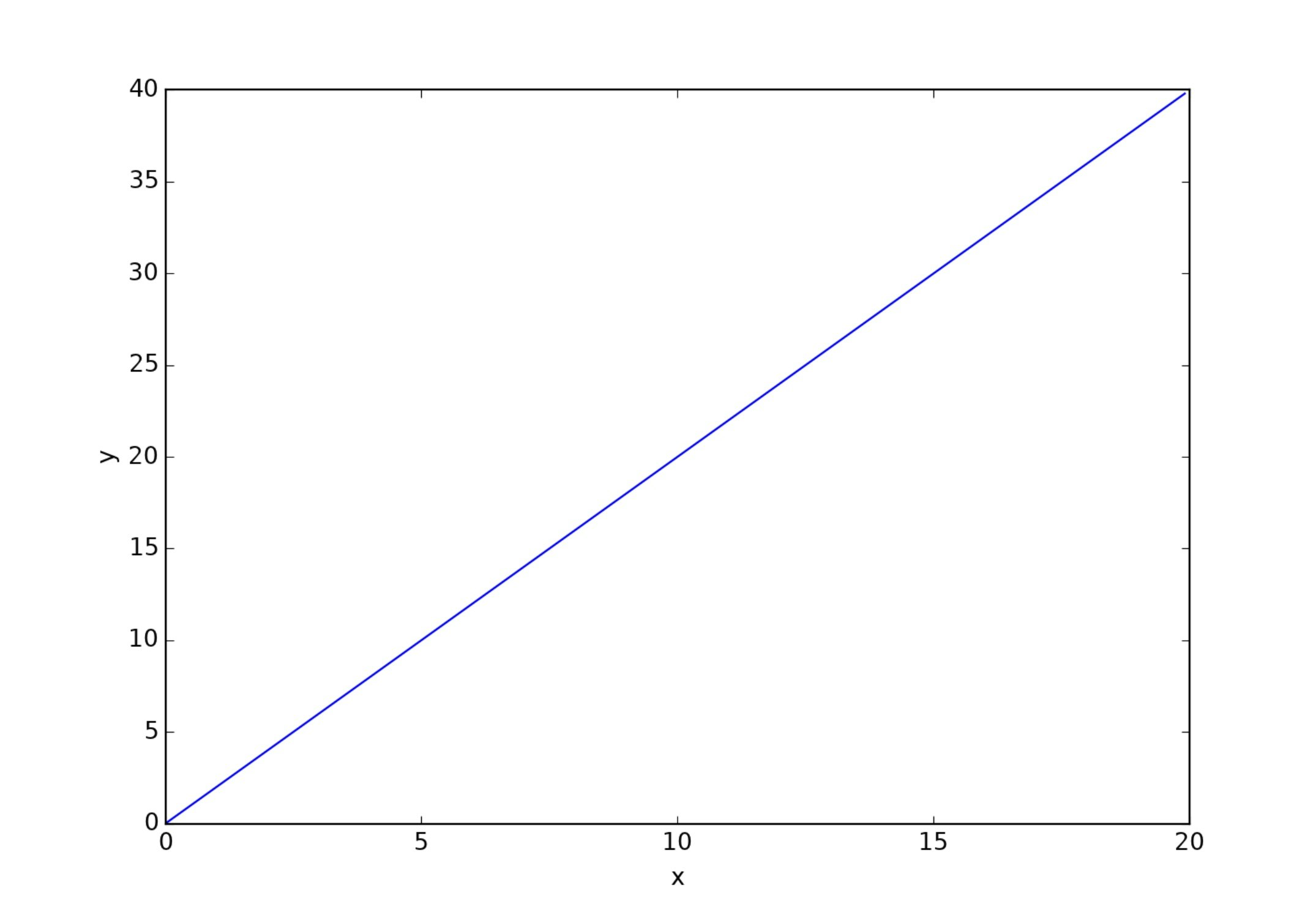

$h$ は丸め誤差を防ぐために $10^{-4}$ 程度にしています。

おまけ

上の数値計算では$$ f^{\prime}(x) = \lim_{h → 0} \frac{f(x + h) - f(x - h)}{2h} \tag{4}$$のように計算すると精度が良くなります。

def nu_dif(f, x):
    h = 1e-4
    return (f(x + h) - f(x-h))/(2 * h)

偏微分

1次元の微分を実装したので、次は多次元の微分を実装しましょう。ここでは簡単のため2次元で微分をします。ある2変数関数 $f(x,y)$ に対して、 $x,y$ それぞれでの微分、すなわち偏微分 $f_x,f_y$ は次のように定義されます。$$ f_x \equiv \frac{\partial f}{\partial x} = \lim_{h → 0}\frac{f(x + h,y) - f(x,y)}{h} \tag{5}$$ $$ f_y\equiv \frac{\partial f}{\partial y} = \lim_{h → 0}\frac{f(x,y + h) - f(x,y)}{h} \tag{6}$$ ここでの関数は $f(x,y)=x^2 + y^2$ としましょう。

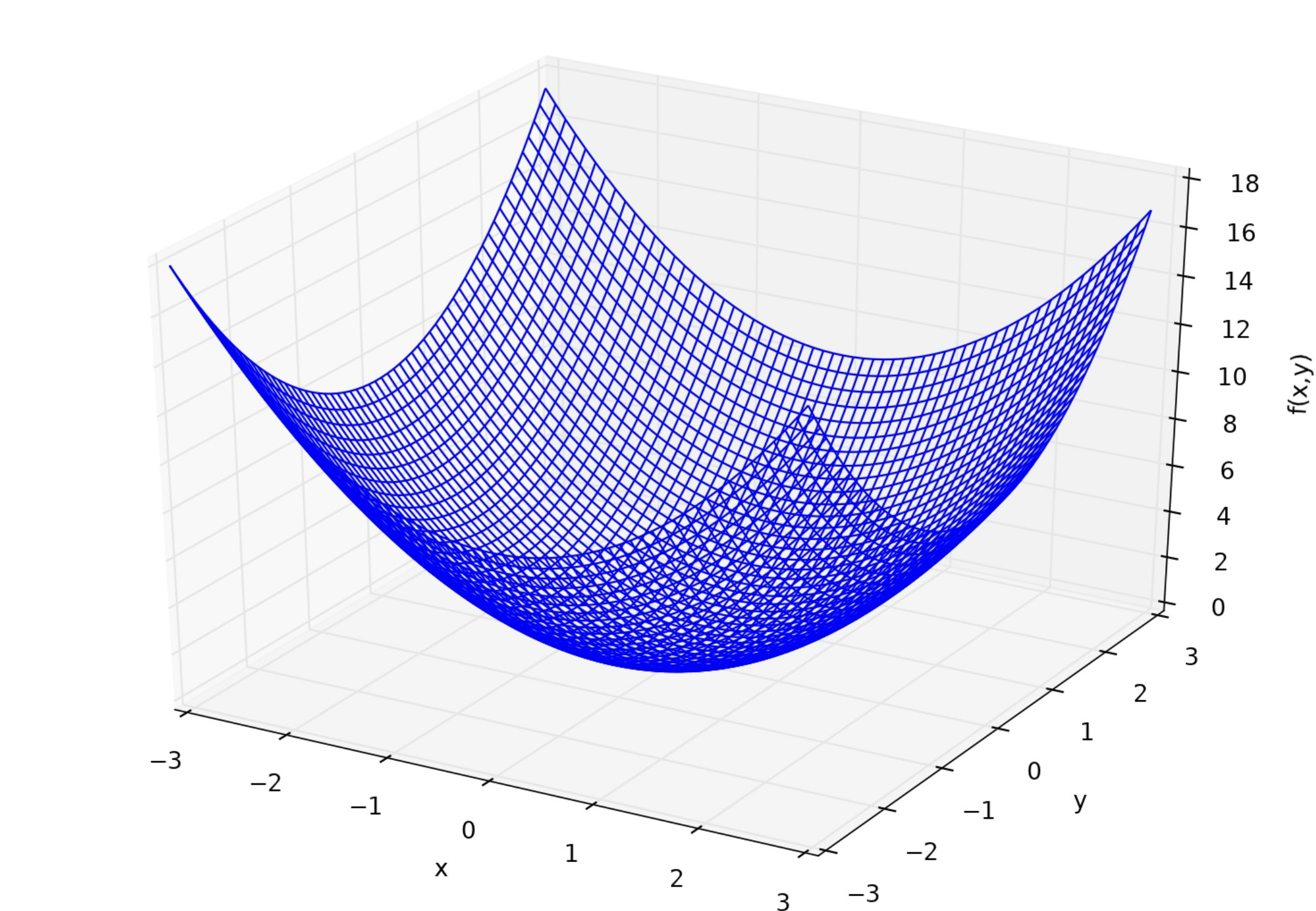
それでは偏微分も実装してみましょう。 $f_x = 2x,f_y = 2y$ となります。

numerical_differentiation_2d.py

def f(x, y):
    return x ** 2 + y ** 2

def nu_dif_x(f, x, y):
    h = 1e-4
    return (f(x + h, y) - f(x - h, y))/(2 * h)

def nu_dif_y(f, x, y):
    h = 1e-4
    return (f(x, y + h) - f(x, y - h))/(2 * h)

勾配(gradient)

3次元デカルト座標における、3変数関数 $f(x,y,z)$ に対する勾配演算子(ナブラ)は$$\nabla f = \bigg(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \bigg) \tag{7}$$で定義されます。スカラー関数にナブラ $\nabla$ を適用するとベクトル量になります。例えば $f(x,y,z) = x^2 + y^2 + z^2$のとき $\nabla f = (2x,2y,2z)$になります。$-\nabla f$ は $f$ の最小値を向きます(厳密には極小値)。また、ナブラは一般に $n$ 次元に拡張できます。
直感的な理解を促すために $f(x,y) = x^2 + y^2$ に対する $-\nabla f = (-2x,-2y)$ を図示します。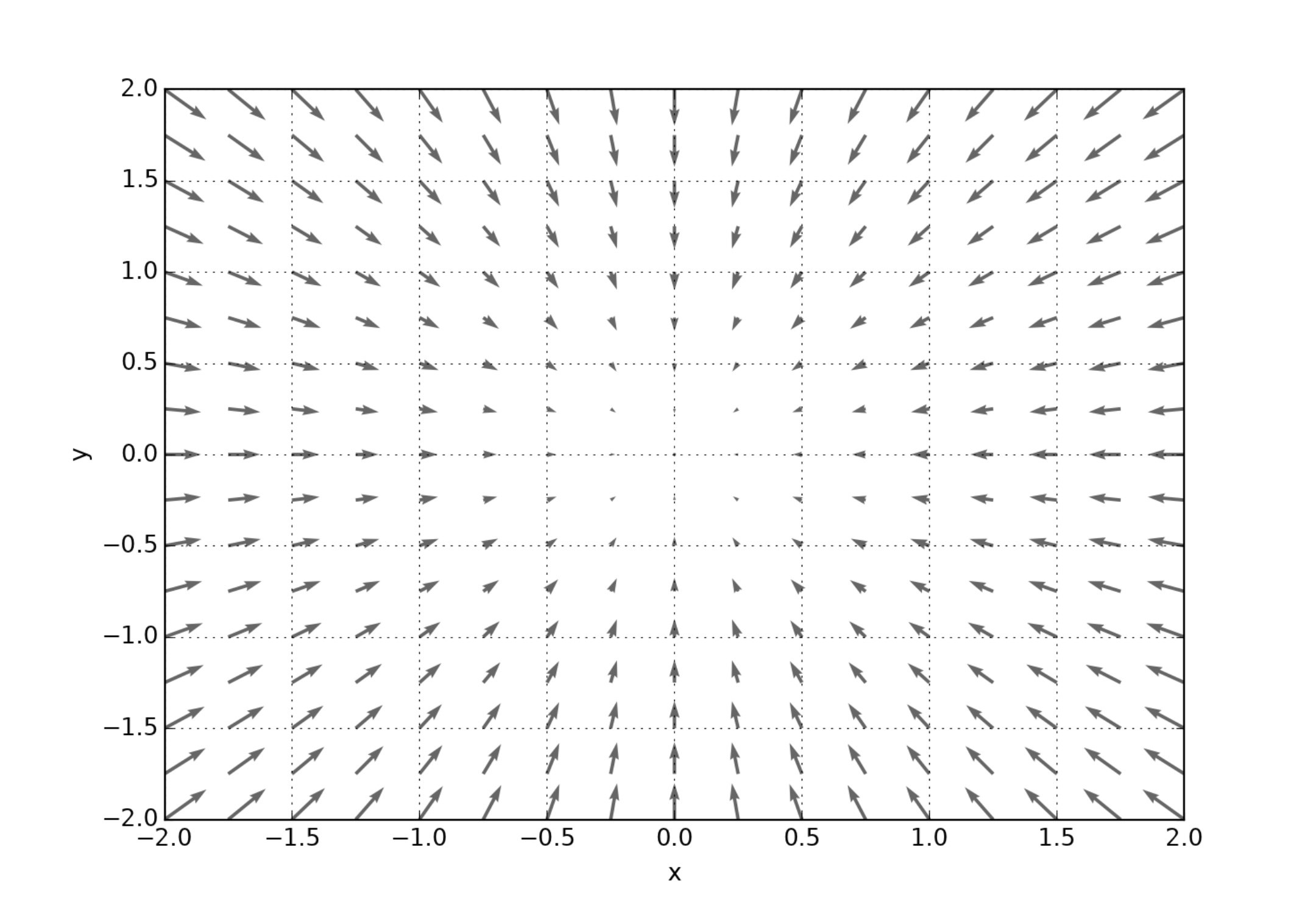
$xy$ 平面状のベクトル $-\nabla f$ はあらゆる点で原点を向いていることがわかります。そして原点における値は $f(0,0) = 0$ で $f$ の最小値となります。矢印の大きさはその点における傾きの大きさを表します。

勾配法の実装

お疲れさまでした。これで簡単な勾配法の実装に必要な数学の基礎は全ておさえました。さあ、自動的に関数の極小値を求めるプログラムを実装しましょう。
任意の点 $\boldsymbol{x}^{(0)}$ からはじめて$$\boldsymbol{x}^{(k + 1)} = \boldsymbol{x}^{(k)} - \eta \nabla f \tag{8}$$ に従って最小値を与える点 $\boldsymbol{x}^* $へ滑り降ります。ここで $\eta$ は学習係数と呼ばれる量で人間が指定しなければいけないハイパーパラメータです。 $\eta$ は大きすぎても小さすぎてもいけない量で適当に調節しなければなりません。今回は学習係数に関する説明は省略します。

それでは勾配法を実装して $f(x,y) = x^2 + y^2$ の最小値を与える点$\boldsymbol{x}^* =(x^* ,y^* )$ を求めましょう。もうすでにわかっている通り $\boldsymbol{x}^* =(0,0)$ が得られれば成功です。

numerical_gradient.py

# fの勾配を返す
def numerical_gradient(f, x):
    h = 1e-4
    grad = np.zeros_like(x)

    for i in range(x.size):
        tmp = x[i]
        x[i] = tmp + h
        f1 = f(x)
        x[i] = tmp - h
        f2 = f(x)
        grad[i] = (f1 - f2)/(2 * h)
        x[i] = tmp

    return grad 

# 勾配法
def gradient_descent(f, x, lr = 0.02, step_num = 200):
    for i in range(step_num):
        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x

# fを定義
def f(x):
    return x[0] ** 2 + x[1] ** 2

# xを出力    
print(gradient_descent(f, np.array([10.0, 3.0])))

$\boldsymbol{x}^{(0)}=(10,3),\eta =0.02,k=0,1,\ldots,199$ とした結果
[ 0.00284608 0.00085382]
が出力されるはずです。 $x,y$ ともに $10^{-3}$ 程度なので殆ど $0$ であると言ってよいでしょう。

機械学習における勾配法

以上では勾配法の概要と効用を説明しました。
機械学習では、とにかく最適な重み $\boldsymbol{W}$ をいかにして求めるかが鍵となります。最適な重みとはすなわち損失関数 $L$ を最小にするような $\boldsymbol{W}$ です。これを求める方法の1つとして勾配法を用いることができます。重み $\boldsymbol{W}$ が例えば $2\times2$ 行列

\boldsymbol{W}=\left(\begin{array}{cc}
w_{11} & w_{12} \\
w_{21} & w_{22} 
\end{array}\right) \tag{9}

で与えられたとき損失関数 $L$ に対して

\nabla L \equiv \frac{\partial L}{\partial \boldsymbol {W}}\equiv\left(\begin{array}{cc}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} \\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} 
\end{array}\right) \tag{10}

を計算して$$\boldsymbol{W}^{(k + 1)} = \boldsymbol{W}^{(k)} - \eta \nabla L \tag{11}$$
に従って勾配法を適用すると $L$ の極小値を与える $\boldsymbol{W}$ が求まります。しかし、大抵の場合求まった $\boldsymbol{W}$ は $L$ の最小値を与えません。目的地にたどり着く前に、落とし穴にハマってしまうようなイメージです。様々な $\boldsymbol{W}$ に対して $L$ の曲面がへこんでいることが多々あります。これを避けるために、もう少し複雑ないくつかの別の方法が存在します。また次回からこれについて書いていきます。

まとめ

ここまで読んでいただいてありがとうございました。
今回は、まず、Pythonを用いた簡単な1次元の微分の実装から始めて、それを多次元に拡張しました。そして、勾配演算子ナブラを導入し、それを用いて任意の関数の極小値を求める勾配法を学びました。そして最後に、勾配法を用いれば損失関数を小さくできる、つまり機械学習の精度が高まることをお伝えしました。しかし、そうして得られる重みはしばしば極値ではあるが、損失関数が最小にならない、つまり最適化されないという問題点があることもわかりました。 次回以降はこの問題に別の方法でアプローチしてみようと思います。

おわりに

今回、友人に紹介してもらってこの千葉大学 Advent Calendar 2019に投稿する機会に恵まれました。かなり初歩的な部分からまとめたので少し大変でしたが、いつもより長々と書いて程よい疲労感と達成感を味わうことができました。
僕の投稿以外にも、いろいろな方が様々なレベルで様々なトピックの素敵な投稿をしているので是非ご覧ください。