【プログラムと証明】線分を描画する「ブレゼンハムのアルゴリズム」を検証する

Status

いまのところ描画と人力での証明のところまで。次は TLA+ か Coq などの定理証明系で証明したい。
ところで、MathJax の垂直位置ずれすぎじゃね？

概要

ブレゼンハムのアルゴリズムとは、ピクセルで表現された画面上に線分を描画するためのアルゴリズムである。
ピクセルの座標は整数値しか持てないため、近似アルゴリズムが必要になる。
そのときに、誤差を持つ浮動小数点演算を行わないで計算を行える点がこのアルゴリズムの長所である。

参考文献

• Wikipedia, ブレゼンハムのアルゴリズム: https://w.wiki/P2G

問題設定

端点 $(x_0,y_0)$ と $(x_1,y_1)$ を結ぶ線分を描画する。ただし、

• 端点は格子点、つまり座標値は整数である。
• 端点はどちらも第一象限にある、つまり、$0<x_0, 0<y_0,0<x_1,0<y_1$ とする。
• 右上に向かう線分である。つまり、$x_0 < x_1, y_0 \le y_1$ とする。なお、水平線を含んでよいが、垂直線は含まない。
• さらに、線分の傾きは $1$ 以下である、つまり、$$\frac{y_1-y_0}{x_1-x_0} \le 1$$ である。

仮定がいろいろついているが、他のケースもすべてこのケースに帰着できるので、こう仮定して一般性を失わない。¹

アルゴリズム

以下、$x_1-x_0 = \Delta x$, $y_1-y_0=\Delta y$ とおく。傾きは $\Delta y/\Delta x$ と表せる。

傾きが $1$ 以下であることから、端点間の整数値の $x$ 座標 $X$ に対して、$y$ 座標 $\hat Y(X)$ を整数になるように計算し、点 $(X,\hat Y(X))$ を描画していけば直線っぽく見えると思われる。
ただし、本来の直線の近似でなければいけないから、本来の $y$ 座標 $Y(X)$ と $\hat Y(X)$ の誤差の絶対値 $|\hat Y(X)-Y(X)|$ が $1/2$ 以下になるようにするとよい。$y$ 座標値を四捨五入しながら描画していくイメージである。

具体例

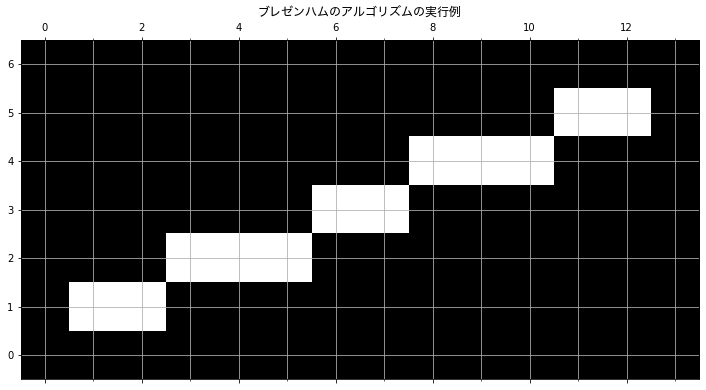
たとえば、$(1,1)$ から $(12,5)$ (傾き $4/11$) への線分を描画するとこのようになる (matplotlib で描いた)。

プログラム

Wikipedia にある最初のアルゴリズムは分数 (deltaerr の分母の $\Delta x$ および if 文の 0.5 の分母の $2$) を使用しているため、浮動小数点演算が必要である。そこで、誤差計算の部分についてすべてを $2\Delta x$ 倍すると、以下のような Python プログラムになる。
なお、grid を NumPy の配列としておくと matplotlib の imshow() や matshow() で描画できる。

def Bresenham(grid, p0, p1):
    def plot(grid, x, y):
        grid[y,x] = 1
    x0, y0 = p0
    x1, y1 = p1
    deltax = x1 - x0
    deltay = y1 - y0
    error = 0
    y = y0
    for x in range(x0, x1+1):
        plot(grid, x, y)
        error += 2*deltay
        if error > deltax:
            y += 1
            error -= 2*deltax
    return grid

先ほどの図は grid = Bresenham(np.zeros((7, 14)), (1,1), (12,5)) として作った配列を描画したもの。

証明

これで線分を近似的に描画できることについて証明する。
以下、$X$ に対する $Y,\hat Y$ の値を $Y(X), \hat Y(X)$ とかく。さらに、誤差 $\hat Y(X)-Y(X) = \varepsilon (X)$ とかく。
証明するのは、$x_0$ と $x_1$ の間のすべての $X$ に対して、$-1/2 < \varepsilon(X) \le 1/2$ であること。右側の不等号のみに等号がついている。
帰納法で証明する:

1. $X=x_0$ のとき、$\hat Y(X) = y_0$ であるため、$\varepsilon(X)=0$ であるから題意を満たす。
2. ある $X$ について $-1/2 < \varepsilon(X) \le 1/2$ であるとする。線分の傾きは $\Delta y/\Delta x$ であるから、もし、$\hat Y(X+1)=\hat Y(X)$ のままにすると、$\varepsilon(X+1) = \varepsilon(X) + \Delta y/\Delta x$ であることと、傾き が $0$ 以上 $1$ 以下であることから $-1/2 < \varepsilon(X+1) \le 3/2$ となる。
3. もし $-1/2 < \varepsilon(X+1) \le 1/2$ の範囲に収まっていればこのままで題意を満たす。
4. もし $1/2 < \varepsilon(X+1) \le 3/2$ ならば、$\hat Y(X+1)=\hat Y(X)+1$ とすることにより、$-1/2 < \varepsilon(X+1) \le 1/2$ とできるので題意を満たす。

以上により、題意は示された。(証明終)

さらに、画面上で連続しているように見えること、つまり、$\hat Y(X+1) - \hat Y(X) \in \{ 0, 1 \}$ であることを示してもよいかもしれない。もっとも、これはプログラムからほぼ自明である。

1. なお、「一般性を失わずに」を、英語では "without loss of generality"、略して "w.l.o.g." とか "wlog" と書くことがある。 ↩