前置き
突然ですが、以下のようなあるリスト source があった時、
>>> source = [0, 1, 2, 3, 4, 5]
このリスト内の要素をランダムにシャッフルして得られるリストを target とします。
例えばこんな感じです。
>>> target = [2, 1, 3, 5, 4, 0]
この時、source と target の間の距離を編集距離を使って測ると、以下のように 4 になります。
>>> from my_utils.algorithm import levenshtein_editops_list
>>> levenshtein_editops_list(source, target)
[('replace', 0, 0), ('replace', 2, 2), ('replace', 3, 3), ('replace', 5, 5)]
この最後の出力の意味は、source から target を得るには、
- source の0番目の要素を target の0番目の要素に置き換える
- source の2番目の要素を target の2番目の要素に置き換える
- source の3番目の要素を target の3番目の要素に置き換える
- source の5番目の要素を target の5番目の要素に置き換える
ことで target が得られる、ということです。
(ここでの置き換えとはリスト内の要素同士の入れ替えとは異なることに注意です。)
置き換え以外にも 要素の削除や挿入といった「操作」があります。
target を得るまでに必要な操作の総数の最小値が編集距離です。
普通は編集距離は文字列同士の距離を測るのに使われるみたいですが、諸事情でリストにしています。多分どちらでも変わりません。
本題
source リストをランダムにシャッフルして target リストを得た時、source と target の間の編集距離の分布 が知りたいです。
厳密に証明を考えるのは大変そうなので、とりあえず実験して様子を見ます。
実験
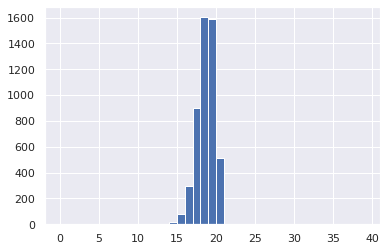
長さ20のリストをランダムに5000回シャッフルしてそれぞれについて編集距離を計算します。
>>> import random
>>> import matplotlib.pyplot as plt
>>> from my_utils.algorithm import levenshtein_list
>>> source = list(range(20))
>>> target = copy.deepcopy(source)
>>> distances = []
>>> for _ in range(5000):
... random.shuffle(target)
... d = levenshtein_list(source, target)
... distances.append(d)
>>> plt.hist(distances, bins=list(range(40)))
今更ですが、リスト同士の編集距離の計算には以下で公開しているソースコードを使っています。
(既存のLevenshteinライブラリを使っているだけですが...wikiにあるアルゴリズムの自前実装よりもこれの方が速かったです。)
結果
最大値は20でした。
これは元のリストの長さの20と同じです。
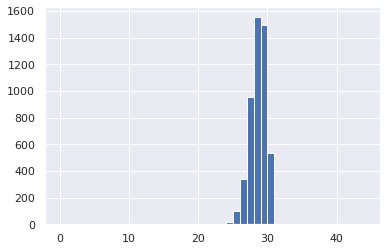
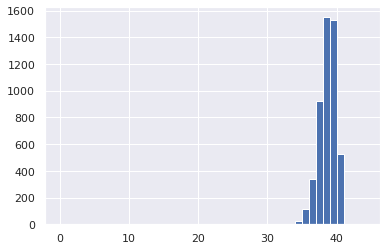
試しに長さが30, 40の時も試しましたが、結果は同様でした。
経験的にですが、リストのシャッフルする前と後の間の編集距離の最大値は、リストの長さと言えそうなことがわかりました。
直感的には、リストの各位置について置き換えを行わなければいけない時に編集距離が最大になる、ということでしょうか。
それから小さい編集距離が全く得られませんでした。不思議です。
おまけに長さが30、40のときの結果を載せておきます。
30の時
40の時
結論
シャッフル前と後の間の編集距離の最大値は リストの長さ かも
ついでにわかったこととして、ランダムにシャッフルすると、編集距離が小さくなる様なリストはほとんど観測されないということがあります。
最大値マイナス6くらいまでしか観測されていません。
例えば編集距離が4などの小さい値になる確率は0ではなさそうなので、最大値付近に比べると限りなく0に近いということでしょうか。
これについて気になったので追加で考察してみます。
考察: なぜ小さい編集距離が観測されないか
簡単のために挿入と削除を忘れて、置き換えが何回必要かの分布を考えることにします。
リストの要素のシャッフルの場合の数は、リストの長さをnとすると、nの階乗$n!$です。
source と target を比べたとき、同じ位置に異なる値が入っている箇所がちょうどk個あるような場合の数 $x_k$ を求めて、それを全ての場合の数$n!$で割れば、置き換えがk回必要となる確率$p(k)$が求められそうです。
まずk個の位置の選び方は$_nC_k$通りです。
選ばれたk個の要素をかき集めて短いリストを作ります。
長さkのこのリストについて、全ての位置にシャッフル前後で違う要素が入っているような場合の数を$a_k$とすると、
x_k = _nC_k a_k
と書けます。
この$a_k$を求めるのに時間がかかったのですが、調べてみるとこの$a_k$には モンモール数 という名前がついていて、kが3以上の時、$a_k$は、
a_k = (k-1)(a_{k-1} + a_{k-2})
という漸化式で求められるそうです(!)。(証明はwikipedia)
$a_0=1$, $a_1=0$から$a_k$が芋づる式にわかります。
a_0 = 1\\
a_1 = 0\\
a_2 = 1\\
a_3 = 2\\
a_4 = 9\\
a_5 = 44\\
a_6 = 265\\
a_7 = 1854\\
a_8 = 14833\\
a_9 = 133496\\
a_{10} = 1334961\\
a_{11} = 14684570\\
a_{12} = 176214841\\
a_{13} = 2290792932\\
a_{14} = 32071101049\\
a_{15} = 481066515734\\
a_{16} = 7697064251745\\
a_{17} = 130850092279664\\
a_{18} = 2355301661033953\\
a_{19} = 44750731559645106\\
a_{20} = 895014631192902121
置き換えがちょうどk回必要となる確率
p(k) = \frac{x_k}{n!} = \frac{_nC_k a_k}{n!}
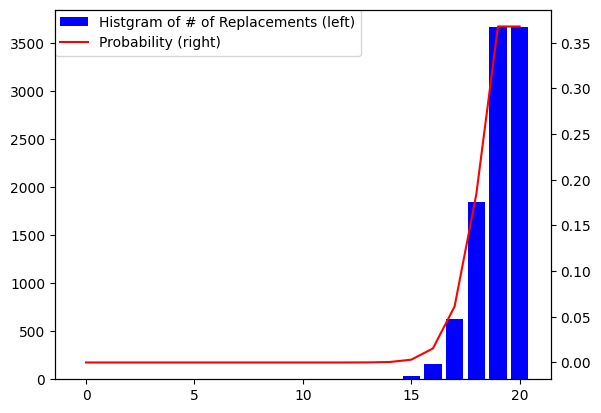
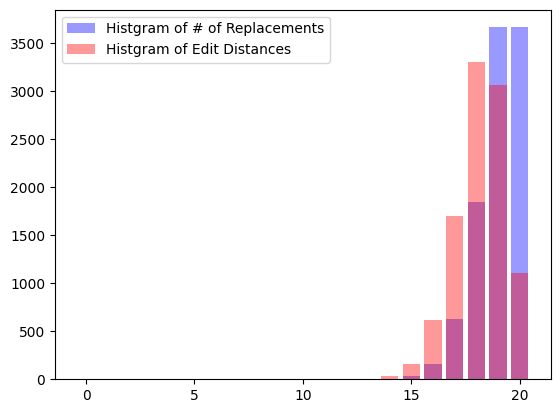
と、実際に集計した値の分布が一致しているかを見てみます。
この様にかなり一致していることがわかり、理論的にも必要な置き換えの回数が少ないときの確率が0に近いことがわかりました。
これの大きな原因としては、モンモール数はkが大きくなるにつれて急激に大きくなっていくことが挙げられると思います。
しかし、下のグラフの様に、実際の編集距離の分布と、必要な置き換えの回数の分布の間には乖離があります。
この問題は、例えば
[0, 1, 2, 3] と [1, 2, 3, 0]は置き換えだけだと4回必要だけど、0の削除と0の挿入の2回の方が少ない操作で編集が可能、といった例があることが原因だと思います。
そのため挿入と削除を考慮しないと実際の編集距離の分布を求めるのは無理そうです。
それっぽい理由がわかってある程度満足したので、この記事はここで終わります。