先日、9月に終了した鳥コンペについて、反省会を開催させていただきました。
(発表資料は俺人さんのブログにきれいにまとめられています。)
私自身は、チームメイトの@daisukelabのおかげで銀メダルを取りましたが、
全く戦力外で、単なる傍観者にすぎませんでした。(お恥ずかしい)
そのため、反省会でも発表する内容がありませんでした。
本稿ではコンペ終了後にlate subして、一矢報いたので内容をご報告します。
今回は異常検知にフォーカスした内容になっております。
鳥コンペとは
ルールはこちらに書きました。ざっくりいうと
- 音データから、264種類の鳥の鳴き声を推測する問題
- 各鳥の音源は9~100個用意されている
- ただし、264種類以外の鳥、もしくは関係のない音の場合、"nocall"ラベルを付与する
nocallは、学習データには含まれないのにも関わらず、テスト時にはラベル付けをしないと
いけません。いわば、nocallは学習データ(正常データ)には含まれない異常データと
見なせます。
そこで、私は異常検知の技術を使ってnocallをあぶりだそうとしたわけですが・・・
コンペの結果は冒頭に述べたとおりです(T T)
本稿の結論
- コンペ中はnocallを検出できなかったが、late sub(コンペ終了後のsub)ではnocallをある程度検出できた
- 一番効いたのはラベル間違い(NoisyLabels)対策
- ラベル間違いに対応できる異常検知手法の選択も重要
nocall
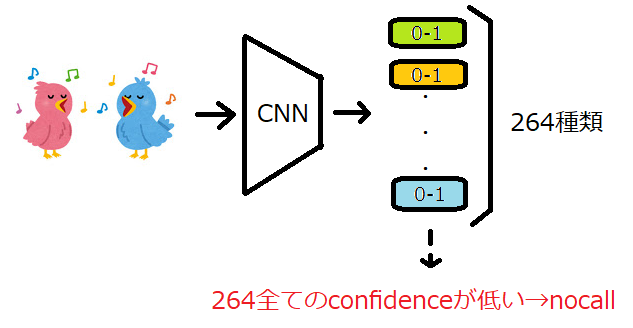
コンペ後に公開されたsolutionを見ると、一般的な解法として、264種類(以降、ターゲット
と呼ぶ)のconfidenceが全て低い場合、nocallラベルを付与していました。
しかし、このような分類器のconfidenceを使って異常を検出する方法よりも、異常検知
手法を使った方が正確に異常検出できることが、こちらの論文で示されています。
コンペ中は「論文の手法(異常検知器)を入れれば、スコアが一気に上がるぜ!」と思って
いました。幸いにも?public LBでは、nocallが54.4%含まれることが分かっており、nocallを
検出できれば、上位を狙えそうでした。
nocallの検出は難しい
再度、nocallの中身を確認しておきます。
- ターゲット以外の鳥の声
- 無音や風の音
- 鳴き声がしてもターゲットか判別できない場合
これらnocallを異常検知器で検出します。
ただ、最後のポイントが曲者で、判定基準が良く分かりません。ラベルを付ける人の耳
次第といっても過言ではなく、判定基準を掴むためのデータセットもありません。
そのため、この判定基準を異常検知器に完全コピーするのは不可能といっていいです。
これだけでもかなりの無理ゲーです。
さらに、前述した論文と異なり、正常が264種類!もあるため、正常範囲が非常に広く
なります。そして、ターゲット以外の鳥の声もテストデータに含まれると予想される
ため、それらを異常検知器で検出しないといけません。つまり、「正常によく似た異常」
(難しい異常データ)が多く含まれます。ますます無理ゲーです。
ということで、冷静に判断すると異常検知器を使ってnocallを検出するのは得策では
ありません。nocall検出よりも、ターゲット分類に注力した方がスコアが伸びる
コンペでした。上位のsolutionを見ても、異常検知のアプローチはありません
でした。(妙に納得感)
nocall検出->何が嬉しいのか?
ということで、無理ゲー、無理ゲーと連呼しておりますが、なぜ、鳥コンペで異常検知に
執着するのか?late subでも異常検知をやったのか?といいますと、一般的な異常検知問題に
置き換えて、以下の可能性が見出せるからです。
- domain shiftしても異常が検出できる
- NoisyLabelsがあっても異常が検出できる
- 正常が264種類あっても異常が検出できる
外観検査に置き換えると、
- 明るい画像を使って、暗い画像でも動く異常検出器が作れる
- 正常データに、ある程度異常データが混じっても異常が検出できる
- 製品群が264種類あっても、数個の異常検知器を用意すれば異常が検出できる
特に、二番目の寄与が大きいと思われ、例えば指が映ってしまったり、ゴミが
混入したりする画像が混じっても、正常に機能する異常検知器が構築できます。
これら3つの特性を持つ異常検知器が構築できると、かなり実戦的な異常検知器といえます。
実務で使える頑強な検知器です。
nocall 攻略法
以上で見てきたようにnocall(=異常)を検出するのは、かなり難しいことが分かりました。
ただ、手段がないわけではありません。結果的に学習(正常)データのみを使って異常
検知器を構築し、スコアを上げることができました。
一つずつ課題を解決していきます。
-
trainとtestで乖離がある
これは、コンペ開催者から説明があったのですが、trainデータはかなりきれいな音源で、
testデータはノイズが混じったり、風の音や飛行機が混じったりする現場寄りの音源で
した。この差が埋めるために、学習中はノイズを付与してノイズが入っても誤作動
しない頑強な異常検知器を構築しました。 -
ラベルが信用できない
コンペ中、ラベルの信用性を若干疑問視していたものの、さほど気にしていませんでした。
しかし、6位に輝いたアライさんのsolutionを見ると、ラベルの信用性(NoisyLabels)を
解決するのが真の課題だったようです。実際、私も異常検知にNosiyLabels対策を入れることに
よって、スコアが上がりました(late subで)。つまり、正常データをそのまま使うと異常
データが混入しているため、異常検知器が誤作動してしまうわけです。具体的な対策
として、NoisyLabels用の損失関数を使うことでスコアが上がりました。 -
正常が264種類ある
正常が2~3種類であれば、1種類ずつの異常検知器を構築して異常を検出する方法が
あります。ただ、今回は正常が264種類あるため、それをやるのは非現実的です
(推論時間の問題)。結果的には正常を3つのグループに分け、各グループで
正常空間を構築しました。 -
正常データが少ない
各鳥の音源は多くて100個です。各鳥で専用の異常検知器を作るとして、そのまま100個
で学習させると過学習の恐れがあります。音源を切り貼りしたり、ノイズを混ぜたりする
ことで、多少DataAugmentationができますが、限界があります。さきほどと重複します
が、そういった意味でも、1種類ずつの異常検知器を構築するのは無理があります。
264種類を3つのグループに分けると、264/3*100=8800音源となり、過学習の恐れが
少なくなります。 -
鳴き声がしてもターゲットか判別できない問題
これだけは攻略法はありません。「音が小さい->判別できないnocall」と判定する方法も
ありますが、全然スコアが伸びませんでした。他のコンペで公開されている
nocallデータセットを入れてみましたが、スコアは上がりませんでした。
ここはそもそも無理ゲーなので、諦めるしかありません。
第1章 全体構成
前置きが長くなりましたが、いよいよnocallを攻略していきます。
前述したとおり、上位のsolutionは以下の構造でした。
- 分類器のconfidence(p)が0.5以上になったものにラベルを付ける(マルチラベル)
- 全てのpが0.5を下回るとnocall判定
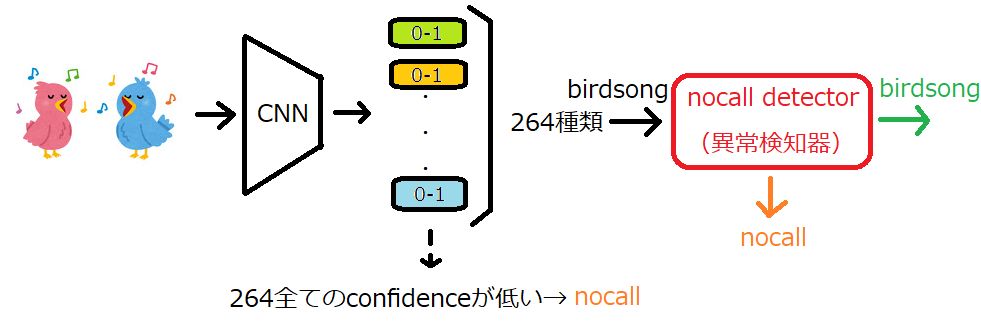
そして、今回は上記の構造に、nocall detector(異常検知器)を追加しました。
- 分類器のpが0.5以上になったもの(birdsong)に対し、nocall detector(ND)を通過させる
- NDで異常度が高いものは、nocall判定
- NDで異常度が低いものは、分類器の推論をそのまま提出
- NDは学習(正常)データで学習させておく
NDを入れることにより、以下のスコア変動が起こります。
①分類器でbirdsong判定(実は間違い)-> NDでnocallに修正してスコアアップ
②分類器でBirdsong判定(実は正解)-> NDでnocallに修正してスコアダウン
③分類器によるnocall判定はNDがあってもなくても変わらない
①をなるべく大きく、②をなるべく小さくすると総合スコアがアップします。
そして、総合スコアがアップすると、ND(異常検知器)が役立ったという
結果になります。(個人的に、一矢報いた結果になります(^^))
第2章 成功した異常検知器
最初に成功した異常検知器をご紹介します。
OE
メインの技術はOutlier Exposure(OE)と呼ばれる外部データを使った
異常検知手法です。(OEの解説記事も現在執筆中です!)
OEは画像のみならず、音データ(DCASE2020 Task2 3rd place solution)
でも優秀な成績をあげており、今後、異常検知の主流になる手法だと思います。
今回はOEの中でも、最新の手法であるBCEを使いました。BCEは「正常
データ」と「正常データと関係ない外部データ」で二値分類させて
学習させます。そして、異常検知方法は外部クラスのconfidenceを異常スコアと
することで異常を検出します。
OE(BCE)の性能を引き出すには、外部データの多様性が重要になります。
(各論文で言われていることですが、OEの外部データは量より多様性が大事です。)
今回、正常データだけで264種類の鳥の鳴き声があるため、肌感覚として、
その倍(264*2=528)の種類の鳥の鳴き声を外部から持ってこないといけません。
しかし、鳥の専門家でない私にとって、528種類の鳥の声を集めてくるのは
容易ではありません。
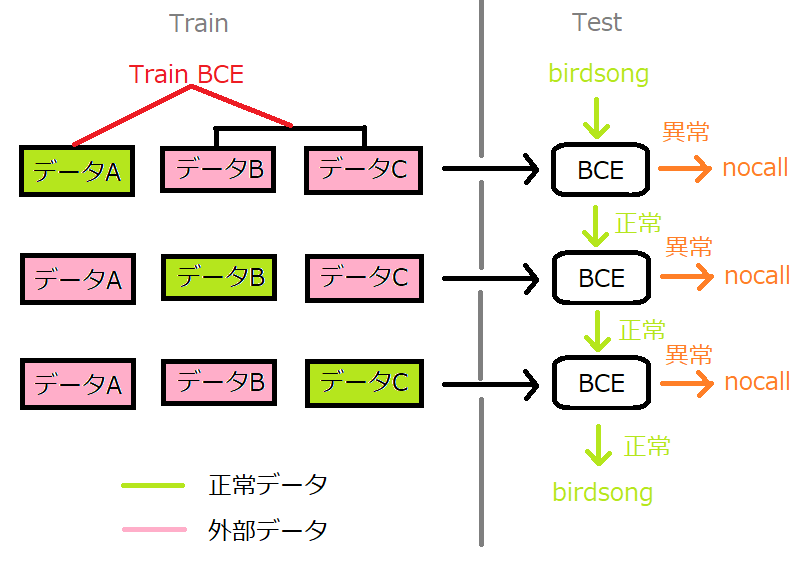
そこで、正常データ264種類を3つのグループ(A、B、C)に分け、例えば、
「正常:A」+「外部:BとC」のように、264種類の中で二値分類が成り立つ
ように学習させました(後述)。これによって「正常:88種類」と「外部:
176種類」のように、外部データの多様性が正常データを上回る仕組みに
なっています。
手順
- 学習データを鳥の種類ごとに3つのグループに分ける(A、B、C)
- A、B、Cがそれぞれ正常となるように学習させると、結果的に3つのBCEができる
- テスト時は3つのBCEを通過させ、一つでも異常と判断された場合は、nocallラベルを付与
- BCEで使う損失関数は、通常のBinaryCrossEntropyの他、NosiyLabels用も使用
最後の損失関数が肝で、今回のデータセットは遠くの方で他の鳥が鳴いていたり、
ラベルの付け忘れをしていたりします。つまり、ラベルが信用できません。
音源によってはグループAの鳴き声が、グループBにも混入している可能性が
あります。(その逆もあり得ます。)
異常検知問題でいうと、「正常データに異常データが混入していたり、BCEで
使う外部データに正常データが含まれたり...」という状況です。(仕事なら
ラベル付け直せ!と言われそうです。)
一般的に、ラベルミス(ラベル間違い、ラベル忘れ)の研究は、NosiyLabels対策
としてかなりホットな研究領域です。今回は、音のNosiyLabels対策用の論文があり、
そこで採用されていた$L_{soft}$と$L_q$を用いました。
結果
まずは何も考えず、そのまま実験をしてみました。
ベースラインは、分類器単体でPrivate 0.598出ています。
これを超えられるかの勝負ですが...
| Public | Private | |
|---|---|---|
| BCE | 0.541 | 0.596 |
| $L_{soft}(\beta$=0.3) | 0.533 | 0.584 |
| $L_{soft}(\beta$=0.7) | 0.549 | 0.587 |
| $L_q$(q=0.3) | 0.546 | 0.595 |
| $L_q$(q=0.1) | 0.528 | 0.595 |
結果的にベースラインを超えられず。
BCEは論文で出てきた形をそのまま(損失関数がBinaryCrossEntoropy)使っています。
$L_{soft}$と$L_q$はデータセットがBCEと同じで、損失関数のみを変更しています。
まさかのBCEが一番スコアが高いという結果になってしまいました。
つまり、NosiyLabels対策の効果がない状況です。
上記の実験では、異常と判断する閾値はp=0.5としていました。
異常と判定する閾値は最適なものがあると考えられ、最後のお願いで、それらを
探索させてみました。やり方は簡単で、validationデータ上でも正常と外部データを作り
精度が一番高くなるような閾値を探索しました。
閾値を探索させた結果は以下のとおりです。
| Public | Private | |
|---|---|---|
| $L_q$(q=0.3) | 0.540 | 0.599 |
| $L_q$(q=0.1) | 0.524 | 0.596 |
最後の最後で、ベースラインを上回ることができました(0.598→0.599)。
ただし、BCE、$L_{soft}(\beta$=0.3)、$L_{soft}(\beta$=0.7)は、閾値がp=1.0というとんでもない値に
なったので、実験は行っていません。
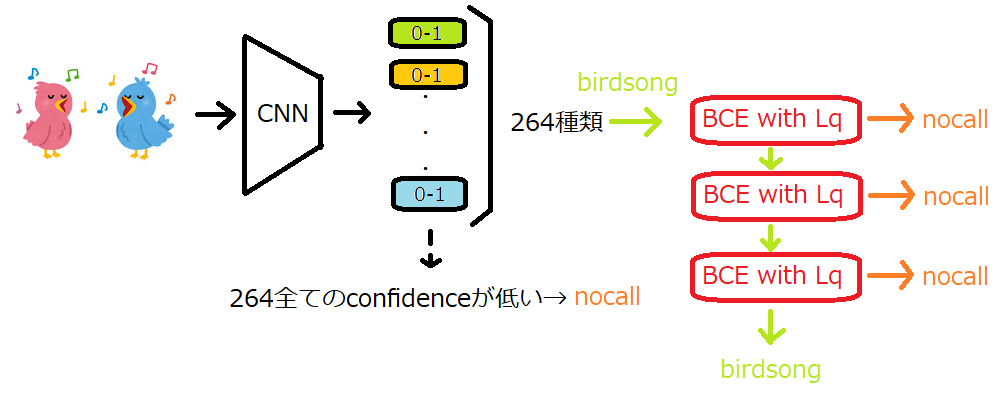
最終構造をおさらいしておきます。
これでPrivateスコア0.599になりました。
第3章 失敗した異常検知器
一応、失敗した方法も明記しておきます。
ArcFace
まずは、クジラコンペやベンガルコンペで活躍してきたArcFaceを使った手法です。
(概要)
- 与えられた学習データを使って、264種類を分類させるようにArcFaceで学習
- Trainデータのembeddingをあらかじめ保持しておき、推論時はそれらとのコサイン類似度で異常(nocall)を検出
- ターゲット以外の音(nocall)の場合は、コサイン類似度が低くなる想定
(失敗原因)
- 学習データが少ない(多くても100個)
- ノイジーラベルが含まれ、ノイジーembeddingを入れるとそこが正常となり、正常空間が歪む
- つまり、ArcFaceを使う前に学習データをクレンジングする必要がある
264モデル
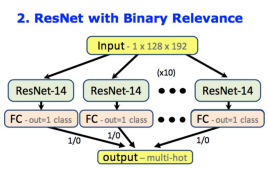
元になったのは以下の論文
Cocktail Party Problem for Bird Sounds
図は論文より引用
- 論文の内容は、鳥が同時に鳴くような状況で、どの鳥が鳴いているのか当てる問題
- 色々手法を検討しているが、鳥の種類分の二値分類器(鳴いている/鳴いていない)で判別するのが一番精度が良かった(上の図)
(鳥コンペに応用)
- 二値分類器を264個用意して学習
- 推論時は全ての分類器で鳴いていないと判定すると、nocallラベルに
(失敗原因)
- 学習データが少なく、完全に過学習していた模様(スコアが0)
- 使うモデルがPANNsのような音専用学習済モデルだと精度が上がる気がするが、処理時間がかかり過ぎる
第4章 理論的背景
一番効果が大きかった$L_q$について、簡単に説明します。元の論文はこちらです。
Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels
通常の分類問題では、損失関数にクロスエントロピーが使われます。
L_{CE}=-\sum_{i=1}^{n} \sum_{j=1}^{c} y_jlogf_j(x_i;\theta)
ただし、cはクラス数、$\theta$はDNNの重みです。
yはラベルでone-hotのベクトルになっているため、ターゲットクラス以外の$y_j$は0です。
また、$f_j$はDNNからの出力で、これは通常ソフトマックス関数が使われます。
$L_{CE}$を最小化すると、分類精度が向上していきます(厳密には最小化->分類精度
向上ではない)。DNNの重みを更新する際は偏微分を使い、式にすると以下になります。
\dfrac{\partial L_{CE}}{\partial \theta }=-\sum_{i=1}^{n}\frac{\nabla_\theta f_{y_i}(x_i;\theta)}{f_{y_i}(x_i;\theta)}(1)
大事なのは分母にfがあることです。fはターゲットクラスの確率(0~1)です。
(1)式より、f(確率)が小さいデータほどDNNの重みの更新に与える影響が大きくなります。
やさしいデータは確率がすぐに1に近づくため、学習開始後、重みの更新に与える影響は
徐々に小さなっていきます。ところが、難しいデータはいくら学習しても確率が小さい
ままで、重みの更新に与える影響が大きいままです。極端にいえば、確率が0に
近づくと更新量が$\infty$になります。
従って、クロスエントロピーは難しいデータ(ハードターゲット)に対して重み付けをする
構造になっています。(個人的にクロスエントロピーの学習速度が速いのは、この重み付けが
大きいと思っています。学習速度が早く、ハードターゲットへの適用を持っているのは
クロスエントロピーの長所といえます。)
ところが、ラベル間違いのデータでは、当然f(確率)が小さいままなので、DNNはfを
大きくすることに注力します。結果的に、正しいラベルを軽視し、ラベル間違いを
重要視する学習になります。そして、**ラベル間違いへの過学習が発生します。**従って、
クロスエントロピーはラベル間違いに敏感な構造をしています。
一方、ラベル間違いに対し頑健な損失関数として、MAEがあります。
L_{MAE}=||y-f(x)||_1
MAEはラベル間違いに頑健な構造を持っています。
(1)式と同じく、偏微分してみると以下になります。
\dfrac{\partial L_{MAE}}{\partial \theta }=-\sum_{i=1}^{n}\nabla_\theta f_{y_i}(x_i;\theta)
(1)式と違い、重みの更新に与える影響は、どのデータでも均等です。ハードターゲット
への重み付けがないため、ラベル間違いがあっても影響はそれほど大きくありません。
MAEは簡単な構造のため、DNNでもすぐに実装できます。しかし、学習が遅くかつ分類精度も
上がらないため、そのままでは使えません。
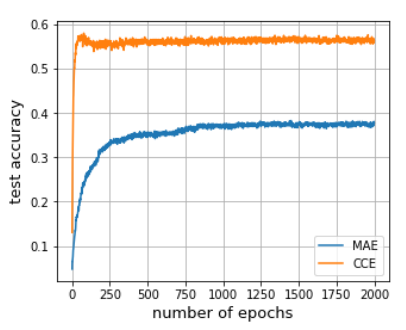
図は論文より引用
図はCIFAR100を普通に学習させた結果です。MAEよりも、CCE(クロスエントロピー)の方が
優れていることが分かります。さらに、MAEは学習の速度も遅いです。(MAEの分類精度が
上がらないのは、クロスエントロピーのようなハードターゲットへの適用がないためと
思われます。理論的に解析した論文が別にあるはずです...)
そこで、論文ではクロスエントロピーとMAEの特性を持つ損失関数$L_q$を提案しています。
\begin{align}
L_q&=\frac{(1-f(x)^q)}{q}\\
&=\sum_{i=1}^{n} \sum_{j=1}^{c} \frac{1-(y_jf_j(x_i;\theta))^q}{q}(2)
\end{align}
重みの更新時、理論的に$Lq$は$q\rightarrow0$だとクロスエントロピー、q=1だとMAEと等価に
なります。qはハイパーパラメータで、論文ではq=0.7を使っています。(鳥コンペでは、
q=0.3を採用しました。)
論文では、$L_q$を採用することで精度を16ポイントほど改善したものもありました。
鳥コンペのBCE(異常検知器)実装では、出力を2クラスのソフトマックスにして
(2)式を適用すればOKです。
さらに、分類器でも$L_q$を適用すると、効果が大きいことが分かりました(後日、
分類器編も書きます)。しかし、分類器の方は264個のシグモイドが並んだような
構造をしています。これはマルチラベルな出力を可能にするためです。そのため、
(2)式をそのまま適用することはできません。少し工夫が必要になります。
まずは、普通のBinaryCrossEntropyを定義します。
def BinaryCrossEntoropy(input, target):
input_ = input# shape=(N,264)
target = target.float()# shape=(N,264) / value is 0 or 1
inputs = input_.view(-1)
targets = target.view(-1)
plus = -targets * torch.log(inputs)
minus = -(1-targets) * torch.log(1-inputs)
return torch.mean(plus+minus)
ラベルが1のときに学習が進むのはもちろんのこと、ラベルが0でも学習できるように
(1-targets)を作っています。
そして、このBinaryCrossEntropyを$L_q$に変更します。
class Lq(nn.Module):
def __init__(self, q=0.3):
super().__init__()
self.q = q
def forward(self, input, target, eps=1e-6):
input_ = input# shape=(N,264)
target = target.float()# shape=(N,264) / value is 0 or 1
inputs = input_.view(-1)
targets = target.view(-1)
plus = torch.pow(inputs * targets+eps, self.q)# 変更!
plus = (1 - plus) / self.q# 変更!
minus = torch.pow((1-inputs) * (1-targets)+eps, self.q)# 変更!
minus = (1 - minus) / self.q# 変更!
return torch.mean(plus+minus)
ただし、epsは値が発散するのを防ぐために入れています。
第2章にも書いたとおり、$L_q$に変えるだけでスコアがかなり上がります。
まとめ
- 異常検知器を追加しても、スコアがほとんど上がらなかったのは残念の極み(そもそも無理ゲー)
- ただ、train/testの乖離やNoisyLabelsの混入があっても異常検知は機能する
- 264個の正常状態の学習は、実務だとあり得ないと思うので、コンペ専用という気がする