遺伝的プログラミングの歴史

はじめに

この記事では，個人的に思った遺伝的プログラミングの革新的な手法についてまとめます．

遺伝的プログラミングとは

遺伝的プログラミング(Genetic Programming; GP)は非常にマイナーな最適化手法の一つです．名前しか聞いたことのない人も数多くいると思います．この節では，遺伝的プログラミング(以後GP)について軽く紹介します．

GPとは，機械学習の目的と同じで，任意の関数を決定する手法です．では，何が機械学習と違うかというと，関数の決定方法に差があります．

• 機械学習 : 求めたい関数の係数パラメータ(重み)を，勾配方向へと更新する

• GP : 求めたい関数を小さな関数の合成関数で表現．小さな関数の組み合わせを最適化する

機械学習と比べたGPの利点は，3つあります．
1つ目は勾配を計算しなくてもよいこと．つまり，勾配を決定できないような問題に対しても応用が利きます(機械学習の場合は，勾配計算ができるように問題を変形させる必要がある)．

2つ目は処理内容がわかりやすいこと．小さな関数(四則演算や三角・対数関数)の組み合わせで，任意の関数を表現しているため，関数の処理手順が比較的明確です．

3つ目は過学習が起きにくい点です．GPは小さな関数の組み合わせを最適化するという手法なため，機械学習と違って過学習を非常にしにくいです(ただし，過学習と探索性のはトレードオフなので，探索性が機械学習よりも悪いという欠点もあります)．

遺伝的プログラミングの現状(2019年3月)

GPの現状を述べると，あんまり流行っていません．これは，機械学習の流行に押されていることや，探索性が機械学習と比べて悪いことが理由としてあるのかもしれません．実応用上では，過学習をしにくい点や，処理内容が分かりやすい点が非常に利点となる場合もあります．

しかし，GPは進化計算の一種なため，探索Seed値による影響が大きく，試行ごとの性能のブレがあります．そのため，コンスタントに性能を発揮できないことが実応用では欠点となります．

まあ，いろいろ言いましたが，結局のところ，「性能がでないから」というのが流行っていない理由になるのでしょう．
とりあえず，これまでのGPの歴史を見てみましょう(個人的解釈あり)．
##遺伝的プログラミングの歴史

Genetic Programming (Koza 1992¹)

GPの元となる理論はこれ以前からありましたが，GPの原著として知られているのはKoza 1992です．なお，Koza 1992は書籍でとなりますので，論文としては，Koza 1994²となります．これを機に，GPの分野は広がっていくこととなります(私はまだ生まれていません)．

このGPの改良手法としてもっとも有名なものはAutomatically Defined Functions(ADFs)でしょう．ADFsは，遺伝子中に参照可能な関数を定義し，全体の木構造を最適化することで，参照可能な関数も最適化されるという手法です．

じつは，ADFsの原著も1992年(by Koza)なので，論文誌によってはGPの原著とADFsの原著の引用文が同じになっていることもあります．

Cartesian Genetic Programming; CGP (Miller 2008³)

「GPの研究者で，ADFsとCGPを知らないやつは，にわか」といっても過言ではないでしょう．

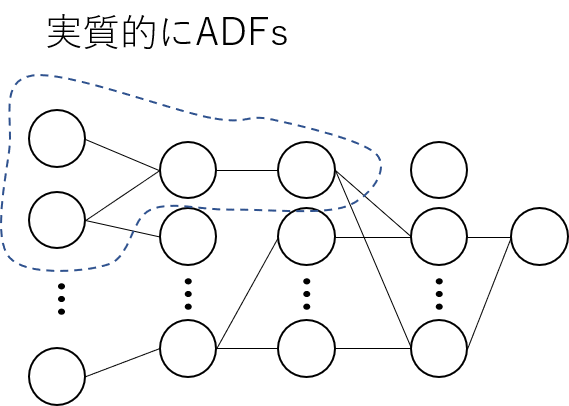
GPとCGPの大きな違いは解表現にあります．一般的に「GP」と言った場合には，木構造の解表現を指します．一方で，「CGP」と言った場合には，フィードフォワード型のネットワーク構造の解表現を指します．CGPのメリットは，フォワード型の恩恵によって自己参照関数定義(ADFs)を自然に組み込むことに成功したことです．これにより，従来の不自然なADFsよりも自己参照関数を最適化するができるようになりました．また，GPの問題点であったブロートについても，遺伝子型の変更によって抑えることができるようになりました．

なお，CGPについても，2008年以前の発表論文(著者は同じ)もありますが，Miller 2008が引用元となる場合が多いです．

Geometric Semantic Genetic Programming; GSGP (Moraglio 2012⁴)

GSGPもGPの歴史を革新させた手法の一つでしょう．初めてこの手法を知った時には，衝撃が走りました．

一言で，GSGPと他のGPの違いを表すならば，「探索対象が違う」ということになります．

通常のGPの探索対象は，「関数」です．もちろん，出力値が目的関数の対象となっていることは自明ですが，ここで重要なことは因果関係です．因果としては 「関数」を変更　→　目的の出力値を得る となります

しかし，GSGPの探索では因果関係が逆転します．つまり，目的の出力値を変更　→　「関数」を得る となるわけです．このため，GSGPは，目的の出力値を探索対象としています．これにより，探索性能が飛躍的に向上しました．

任意の出力値を得る関数を生成できるの？と疑問に思う人もいるでしょう．もちろんそんなことはできません．しかし，二つの関数が出す，各出力値間を結ぶ直線上の，出力値を吐き出す関数なら生成可能なのです！(何言ってるかわからない)

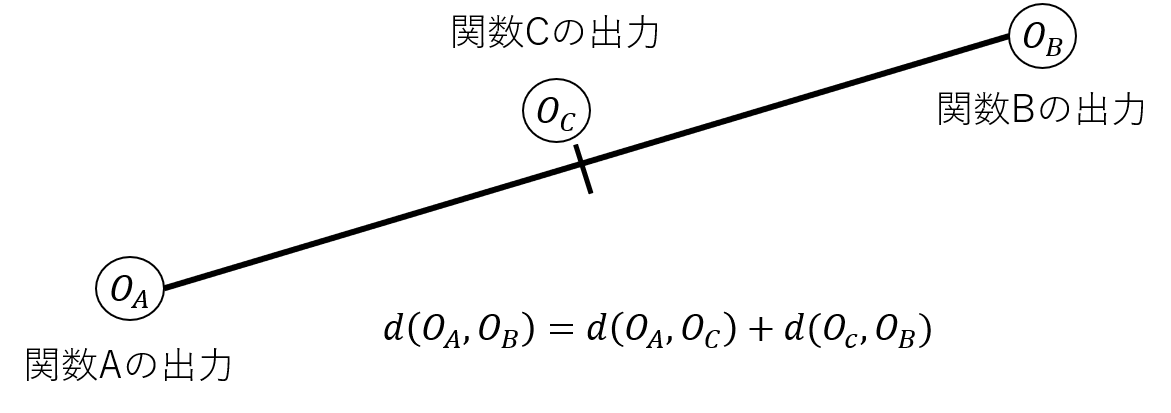
初見では，GSGPの説明は非常に難解なものとなります．そのため，ここまでの説明にし，また別の記事を書くことにします．

さて，GSGPはGP界隈を大きく揺らしました．その結果，2012年以降はGSGPの派生手法がいっぱい出てきます．しかし，GSGPには大きな欠点が2つも存在しました．

1つ目は，向上しすぎた探索性能による過学習です．これは，探索空間を構造の変形から，出力値の変形へと換えてしまったことに依存しています．「GSGPは過学習する」こんな主張もよく見ます．

2つ目は，処理内容の不透明化です．GSGPは，出力値に合わせて，合成関数を変更します．このとき，接ぎ木の様な手法で合成関数を変更するため，木の大きさが爆発的に大きく，複雑になってしまいます．これではGPの利点の一つであった，「処理内容がわかりやすいこと」が無くなってしまいます．現状では，ルールベースのシステムによって，大きくなった木を簡単化する手法が一般的です．

ε-Lexicase Selection; EPLEX (William 2016⁵)

GSGPの波の中で生まれた手法がEPLEXです．なお，EPLEXの前身となるLexicase Selectionは2012年の時点で発表されています(共著者)．では，Lexicase SelectionとEPLEXは何が違うのでしょう．

この違いは，適用できる問題にあります．Lexicase Selectionは整数回帰問題(Logical Circuit Regressionなど)にしか適用できませんでした．一方で，EPLEXは実数回帰問題(一般的なRegression Problem)への適用が可能となったのです．これにより多くの問題での性能検証が行えるようになりました．

2018年のGECCO Best Paperに選ばれた「Where are we now? A Large Benchmark Study of Recent Symbolic Regression Methods⁶」では，多くの問題⁷に対して，EPLEXが一般的な機械学習の手法やXGBoostと比べても優位な性能を誇ることが書かれています．(ただし，汎用的なパラメータチューニングを行っているため，個々の問題に対してチューニングした場合の結果は不明)

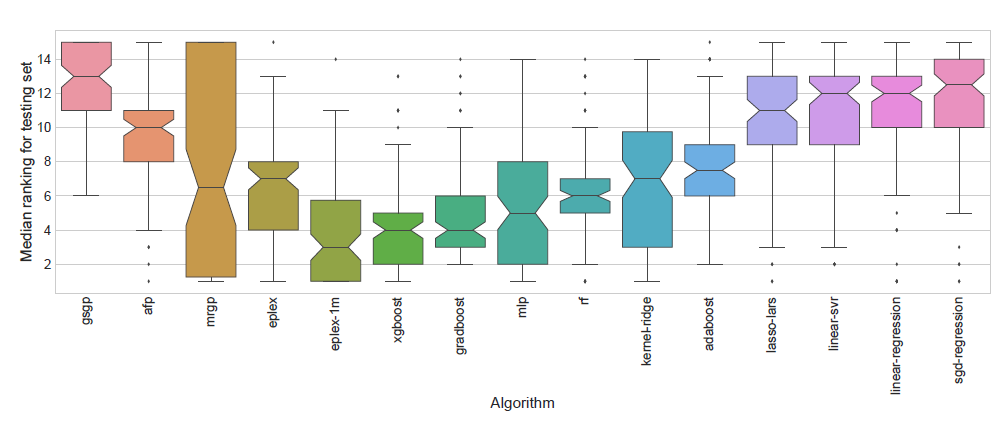
(⁶より引用．低いほど良い．図中のeplexとeplex-1mがEPLEXによる性能．eplex-1mはGPの集団サイズと世代数を増やしたもの)

EPLEXの重要なことは，個体を選択する際のデータを確立的に選ぶことにあります．あれ？どっかで聞きましたね．そうです．機械学習でおなじみのStochastic Gradient Descent(SGD)と発想の根幹は同じです．

SGDのオンライン学習をGPでやっていると考えれば，機械学習をやっている人にはわかりやすいかもしれません．しかし，機械学習と違って，GPは多点探索手法です．そこで，この「データを確立的に選ぶ」という動作を行うと，非常に多様性に優れた探索が可能となるのです．

実は，もともとGPはGenetic Algorithm(GA)と違って，非常に多様性の損失が早いアルゴリズムです．そのため，集団サイズを増やしてもを用意しても，早期収束してしまうという問題点を抱えていました．これが，EPLEXの導入によって解決されたのです．

EPLEXも詳しいアルゴリズムの解説も長くなってしまうため，また今度にします．

また，EPLEXにも欠点があります．それは，「計算量が大きすぎる」という点です．一般的に使われる選択オペレータの計算量は，

• ルーレット選択 : 最悪計算量 = $N$(母集団の数だけ繰り返す) × $N$(一回ルーレットを回す) = $O(N^2)$
• トーナメント選択 : 計算量 = $N$(母集団の数だけ繰り返す) × $M$(トーナメントサイズ) = $O(NM)$
• EPLEX : 最悪計算量 = $N$(母集団の数だけ繰り返す) × $N$(集団の数) × $T$(データ数) = $O(N^2T)$

となります．さらに，ルーレット選択の最悪計算量はほとんど起こらないのに対して，EPLEXの最悪計算量は，解収束が進むと発生確率が増加します．また，計算量がデータ数に依存してしまう点も問題視されており，大きなデータ数を持つ問題を解く際には，非常に時間がかかってしまいます．実際，EPLEXを使うと，関数本体の計算時間よりも選択オペレータの計算時間が長いことは多いです．この問題点は，Batchの概念をEPLEXに入れてあげることで改善するかもしれません(予言)．

おわりに

GPの歴史をまとめてみました．実際にはまとめきれないくらいの派生・改善手法が提案されているのですが，今回はこれぐらいにしておきます．そして，GPが流行っていない理由であった，「性能が出ない」は，もうすぐなくなります．実際，機械学習との性能差は少なくなっているのです．もちろん，今回のまとめは，個人の解釈が入っているため，より有名な手法や革新的手法が抜けている場合があります．ご注意ください．

また，紹介した手法はGPの派生・改善手法なため，BlackBox Optimizationの一部です．そのため，すべての手法にはNo Free Lunchの定理⁸が適用されることを忘れてはいけません．そのため，記事中で紹介した，「Where are we now? A Large Benchmark Study of Recent Symbolic Regression Methods⁶」の性能も，適用対象⁷の問題系に依存した結果となります(もちろん機械学習の各手法もNo Free Lunchの定理が適用されます)．

1. Koza John R., Genetic programming: on the programming of computers by means of natural selection, MIT press, 1992. ↩

2. Koza John R., Genetic programming as a means for programming computers by natural selection, Statistics and computing, 4.2, pp. 87-112, 1994. ↩

3. Miller Julian Francis, Simon L. Harding, Cartesian genetic programming, In: Proceedings of the 10th annual conference companion on Genetic and evolutionary computation, ACM pp. 2701-2726, 2008. ↩

4. Moraglio Alberto, Krawiec Krzysztof, Johnson Colin G,Geometric semantic genetic programming, In: International Conference on Parallel Problem Solving from Nature, Springer, Berlin, Heidelberg, pp. 21-31, 2012. ↩

5. La Cave William, Spector Lee, Danai Kourosh, Epsilon-lexicase selection for regression, In: Proceedings of the Genetic and Evolutionary Computation Conference 2016, ACM, pp. 741-748, 2016. ↩

6. Orzechowski Patryk, William La Cava, Jason H. Moore, Where are we now? A Large Benchmark Study of Recent Symbolic Regression Methods, Proceedings of the Genetic and Evolutionary Computation Conference 2018, pp. 1183-1190, 2018. ↩ ↩² ↩³

7. Penn Machine Learning Benchmarks https://github.com/EpistasisLab/penn-ml-benchmarks ↩ ↩²

8. Wolpert David H., William G. Macready, No Free Lunch Theorems for Optimization, IEEE transactions on evolutionary computation 1.1, pp. 67-82, 1997. ↩