はじめに
最近,機械学習には過学習を超えた先にも学習があるという話を後輩から聞いたので,それについて検証してみます.
どういうこと?
この話はもともとReconciling modern machine learning and the bias-variance trade-off1という論文から来ました.
論文中では,次のようなことが示されています.(論文1より)
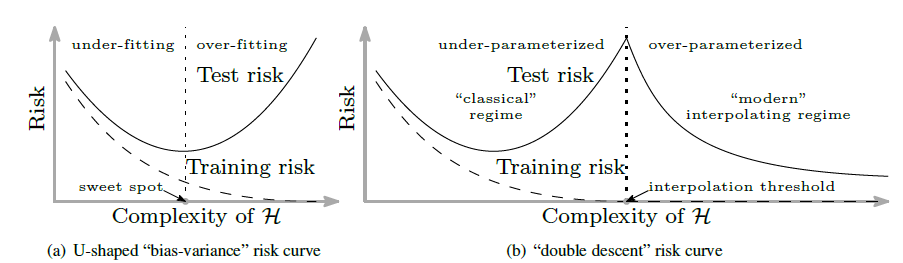
Figure 1: Curves for training risk (dashed line) and test risk (solid line). (a) The classical U-shaped risk curve arising from the bias-variance trade-off. (b) The double descent risk curve, which incorporates the U-shaped risk curve (i.e., the “classical” regime) together with the observed behavior from using high complexity function classes (i.e., the “modern” interpolating regime), separated by the interpolation threshold. The predictors to the right of the interpolation threshold have zero training risk.
つまり,今ままでの機械学習の理論ではモデルの複雑性を上げると,学習リスクが上がる(過学習する)けれども,さらにモデルの複雑性を上げていった場合には,学習リスクが再度下がると言っているのです.さらに,理論上ではモデルの複雑性を上げれば上げるほど,リスクは低下するので「過学習なんてしないんだぞ!」って話です.
詳しい内容は論文を読んでみてください.
https://arxiv.org/abs/1812.11118
検証
論文中にはRandom Forestについて次のような結果が得られたと書いてあります.
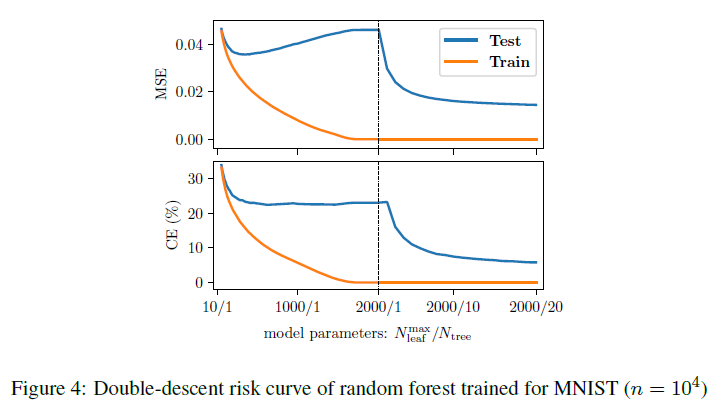
たしかに,上記で見せたようなDouble-descent risk curveが見えます.
しかし,$N_{tree}$を増やしてもいいのでしょうか?(図中右半分)
当たり前ですが,$N_{tree}$(木の数)を増やせば,RandomForestはアンサンブルモデルなので,過学習しにくくなります.また,木の数を増やせばパラメータ数は増えるので,上記の理論と一致しています.
しかし,これでは過学習を超えた先というよりも,「アンサンブルしてね」という話になってしまいます.
そこで,$N_{tree}$を増やさずにパラメータを増やした場合を検証してみます.
注意:(論文中ではNeural Networkについても同様の実験および結果を出しています.そのため,上記のDouble-descent risk curveが間違っているという話ではないです)
検証環境・内容
- scikit-learn
- RandomForestClassifier
- MNIST
- 80% training, 20% test
- $N_{tree}$
- n_estimators : 2, 3, 4
- $N^{max}_{leaf}$
- max_leaf_nodes : [2,50000]
program
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier as rf
from sklearn import datasets
from sklearn.model_selection import train_test_split
import pickle
mnist = datasets.fetch_mldata('MNIST original')
features = mnist.data / 255
target = mnist.target
test_size = int(len(target)*0.2)
train_features, test_features, train_target, test_target = train_test_split(features, target, test_size=test_size)
result = {}
for n_estimators in range(2,5):
for max_leaf_nodes in range(2, 50000):
arg = {"n_estimators":n_estimators, "max_leaf_nodes":max_leaf_nodes}
model = rf(**arg)
model.fit(train_features, train_target)
train_score = model.score(train_features, train_target)
test_score = model.score(test_features, test_target)
result[(n_estimators, max_leaf_nodes)] = {"trian":train_score, "test":test_score}
f = open("rf_leaf_nodes_result","wb")
pickle.dump(result, f)
f.close()
検証結果
それぞれ,木の数が2,3,4のときに$N_{tree}$(=max_leaf_node)を増やしした結果.
試行平均とってないせいで,scoreがぶれて,グラフの線が太くなってる(気が向いて結果取り直したら修正します).
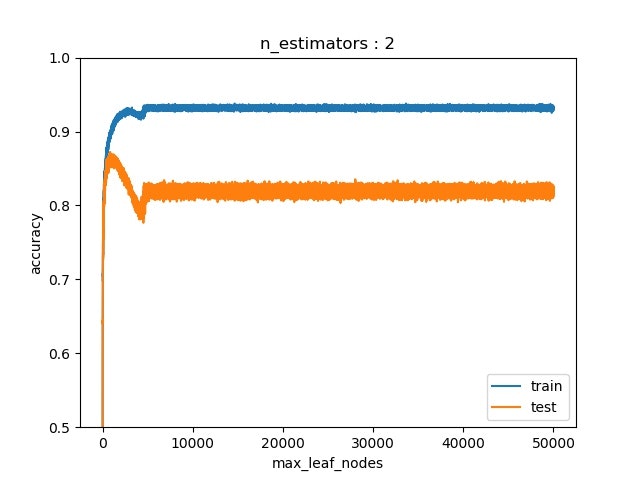
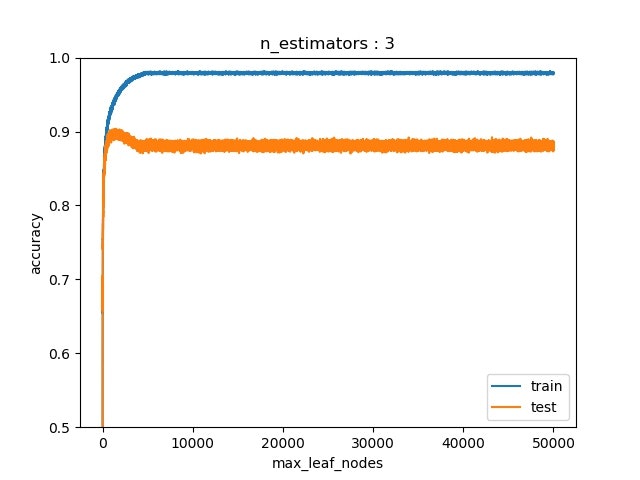
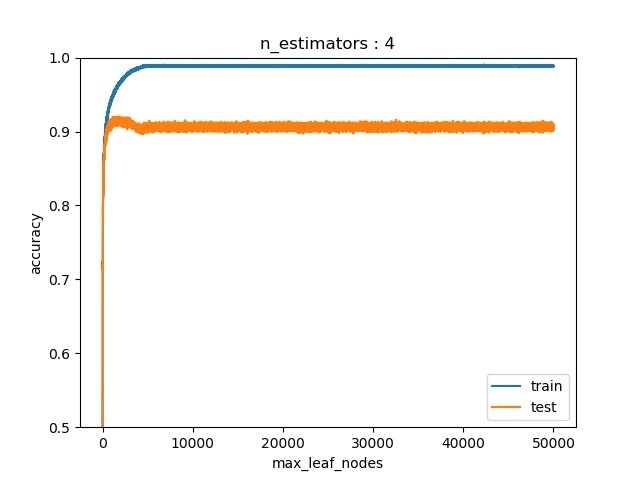
木の数が4以上だと,過学習がほとんどしないので,それ以上増やした時の結果はなし.
木の数が2のときが一番顕著にDouble-descent risk curveが表れている(この場合はaccuracyなのでrisk curveじゃないけど).
たしかに一度過学習した後に持ち直す様子が見える.しかし,論文中で話していた,「パラメータを増やすとリスクが0になる」様子は確認できなかった.つまり,パラメータを増やしすぎた場合には,過学習した.
まとめ
機械学習には過学習を超えた先にも学習があるという話を検証してみた.
この結果,たしかに過学習した後に持ち直す学習が存在した.
しかし,この過学習後の学習は,過学習する前よりも結果的には悪い.
おわりに
今回はRandom Forestで過学習のその先を見てみました.しかし,一般的にはRandom Forestで木の数を4以下にすることはないので,実用的ではないでしょう.時間があったらNeural Networkでも検証してみます.