LaLondeデータセットに対して EConMLのDoubly Robust 推定を使って因果推論

はじめに

前回書いた記事LaLondeデータセットに対し傾向スコア（IPW）をPythonで実装して因果推論では、就労支援の効果に関する（人為的に作り出した）観察データであるLaLondeデータセットに対して、傾向スコアによる逆確率重み付き推定（IPW）で因果効果を推定しました。このデータでは対照群のデータ件数が多い不均衡データであるため、対照群のサンプルは大半が0に近い傾向スコアとなり、これの逆数である重みはわずかな誤差で不安定となってしまうことが原因でした。

今回は、傾向スコアとIPWを使った手法の発展形である Doubly Robust 推定を実施してみます。この推定をPythonで実施する際には、MicroSoftが提供しているライブラリ EconML を使います。初めにDoubly Robust 推定について説明して、それからEConMLを使って実際に就労支援の効果を推定します。
前回説明したので、今回はLaLondeデータセットなどに関しては説明しません。興味ある方は前回の記事をご参照ください。

Doubly Robust 推定

IPWでは介入群に対する効果を以下のように推定しました。
$$
\frac{1}{N} \Sigma_i \frac{z_i y_{i}}{\hat{e}_i} \quad \quad (1)
$$

ここで、

• $N$ : データの標本数
• $z_i$ : $i$番目の人の介入ダミー変数。就労支援を受けていれば1、受けていなければ0
• $y_i$ : $i$番目の人の'78における収入
• $\hat{e}_i$ : $i$番目の人の推定された傾向スコア

Doubly Robust 推定では以下の推定量を用います。

$$
\tau_1 = \frac{1}{N} \Sigma_i [ \frac{z_i y_i}{\hat{e}_i} + ( 1 - \frac{z_i}{\hat{e}_i} ) \hat{m}(x_i) ] \quad \quad (2)
$$

ここで $\hat{m}(x_i)$は回帰分析などで推定された因果効果量です。前回の例では線形モデルを仮定して推定していました。
この$\tau_1$は、以下の２つのうちどちらか1つの条件が満たされていれば、$E[\tau_1] = E[Y_1]$ となることが知られています。ここで$Y_1$は介入が入ったときの結果変数（ここでは'78の収入）です。

• 因果効果のモデルが正しく推定されている、すなわち $\hat{m}_1(X) = E[Y_1|X] $
• 傾向スコアが正しく推定されている、すなわち $\hat{e}(X) = P(Z=1|X)$

この意味で、Doubly Robust （二重に頑健）な推定という名前がついています。この記事の末尾に、一応証明を付けておきました。興味がある方はご参照ください。

EConML

Doubly Robust など、複雑な因果推論を実行するライブラリとして、Microsoftが提供しているEConMLがあります。EConMLのドキュメントはこちらです。
実験データ、観察データどちらの因果推論もできるようになっています。
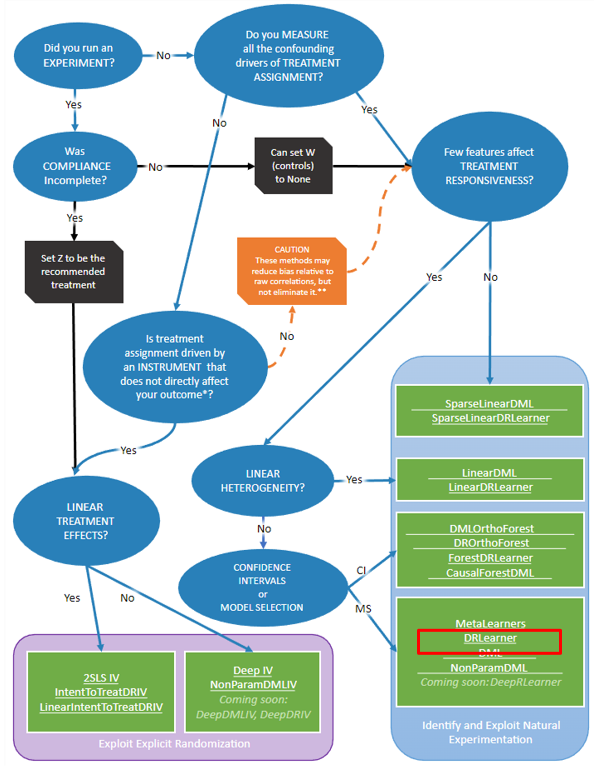
Doubly Robust 以外にも、いろんな手法が用意されています。どのような時に、どの手法を使うべきかを選択できるようにライブラリのフローチャートが用意されています。

ただし、このフローチャートでは因果推論の用語が使われていますので、正しい方法を選ぶためには基礎知識は必要となっています。

今回はDoubly Robust を実行する DRLearner に焦点を絞ります。

線形モデルとロジスティックでDoubly Robust

EConMLのDRLearnerを使って、まずは以下のモデルで推定してみます。

• 因果効果モデル：線形モデル
• 傾向スコアモデル：ロジスティック回帰モデル

始めに、前回同様NSWとCPSのデータを読み込み、LaLondeデータセットを作ります。

nsw_data = pd.read_stata("https://users.nber.org/~rdehejia/data/nsw_dw.dta")
cps1_data = pd.read_stata("https://users.nber.org/~rdehejia/data/cps_controls.dta")
nsw_cps1_data = pd.concat( [nsw_data.query("treat==1"), cps1_data], axis=0 )

このデータに対して、LinearDRLearnerを実行します。

from econml.dr import DRLearner, LinearDRLearner
from sklearn.linear_model import LinearRegression, LogisticRegression

X = nsw_cps1_data[['age', 'education', 'black', 'hispanic', 'married', 'nodegree', 're74', 're75']]
y = nsw_cps1_data['re78']
T = nsw_cps1_data['treat']

est = LinearDRLearner(
  model_propensity=LogisticRegression(max_iter=10000, penalty='none', random_state=1),
  model_regression=LinearRegression(), 
  random_state=2, cv=5)

est.fit(y, T, X=X, W=None)

fit()メソッドでモデルを推定しています。推定したモデルを使って因果効果を計算するときはate()メソッドを使います。

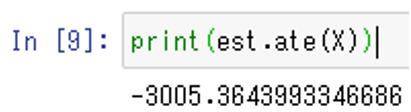
print(est.ate(X))

就労支援の介入により、収入は3005ドル減少したと推定されてしまい、実際とは逆の結果となっています。
前回、因果効果のモデルとして線形モデル、傾向スコアとしてロジスティック回帰モデルをそれぞれ使い、推定された因果効果は真の値からはずれていることを見ました。このモデル２つを同時に使っても、モデルの当てはまりが改善されるわけではないのでしょう。Doubly Robustは因果効果モデルと傾向スコアのどちらか１つが正しければ、良い推定量となります。２つとも当てはまりが悪い場合は、結局良い推定量とはならないことを確認したことになったようです。

ランダムフォレストでDoubly Robust

次に、以下のモデルの組み合わせでDoubly Robust推定を実施します。

• 因果効果モデル：ランダムフォレスト回帰モデル
• 傾向スコアモデル：ランダムフォレスト分類モデル

それぞれのランダムフォレストモデルのハイパーパラメータはGridSearchで決定することにします。
EConMLのDRLearnerを呼び出す前にGridSearchを実行する関数を定義しておき、以下のように実装します。

from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.model_selection import GridSearchCV

model_reg = lambda: GridSearchCV(
                    estimator=RandomForestRegressor(random_state=1),
                    param_grid={
                        'max_depth': [3, 5, 10],
                        'min_samples_leaf':[10,20,50],
                        'n_estimators': (100, 200, 500)
                    }, cv=5, n_jobs=-1, scoring='neg_mean_squared_error'
                )
model_clf = lambda: GridSearchCV(
                estimator=RandomForestClassifier(min_samples_leaf=10, random_state=1),
                param_grid={
                        'max_depth': [3, 5, 10],
                        'n_estimators': (100, 200, 500)
                     }, cv=5, n_jobs=-1, scoring='neg_mean_squared_error'
                )
est3 = DRLearner(model_regression=model_reg(), model_propensity=model_clf(),
               model_final=model_reg(), cv=5, random_state=1)
est3.fit(y, T, X=X, W=None)

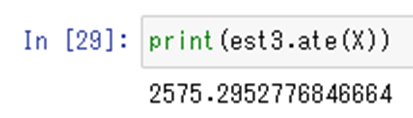
est3.ate(X)

今度は、就労支援の介入効果で、収入は2575ドル増加したと推定されました。真の値1794ドルからはずれていますが、介入によって収入が増えたという結果が得られました。

まとめ

この記事では、LaLondeデータセットに対してEConMLのDoubly Robust推定を実施しました。
因果効果について線形モデル、傾向スコアについてロジスティック回帰モデルを使った場合、モデルの当てはまりがよろしくないようで、Doubly Robust推定量$(2)$は良い推定量ではありませんでした。
モデルを少し複雑にし、因果効果についてランダムフォレスト回帰モデル、傾向スコアについてランダムフォレスト分類モデルを使うと、介入の効果があったという結果が得られました。

ただし、ランダムフォレストを使った結果でも、乱数（random_state）を変えると、因果効果の数値は2500ドル～5000ドルと変わってしまいました。おそらく、Doubly Robust推定と機械学習モデルを組み合わせても過信は禁物で、汎化性能などを検証しないと正しい結論は得られないと思います。

EConML自体はドキュメントもそれなりに充実していて、扱いも困難ではなく、因果推論を実施する必要が生じたときは有用なライブラリだと思いました。ただし、正しく使うためには扱っている対象の背景の理解、データの理解、モデルの汎化性能の検証などをしっかりやらないと、誤った結果を導いてしまう危険性もあると思いました。

参考

EConML LinearDRLearner
EConML DRLearner
GridSearchの利用方法は EConMLのこのページの下部を参考にしています。
岩波データサイエンスVol.3

参考 式(2) が二重に頑健な推定量であることの証明

前提

強く無視できる割り当ての仮定が成り立っているものとする。
$ \{ Y_1, Y_0 \} \perp Z | X$

これは、共変量Xが与えられれば、$Y_1$と$Y_0$は介入群と対照群のどちらに割り当てられるかによらずに決まることを意味しており、結構強い仮定です。

証明

\tau_1 = \frac{Z}{\hat{e}(X)}Y + (1 - \frac{Z}{\hat{e}(X)}) \hat{m}_1(X)

$\tau_1$は下式のように書き換えられます。

\tau_1 = Y_1 + \frac{Z - \hat{e}(X)}{\hat{e}(X)}(Y_1 - \hat{m}_1(X))

ここで、$Y=Z Y_1 + (1-Z)Y_0$ 、 $Z(1-Z) = 0$を使っています。

この右辺第2項の期待値が0になれば、$E[\tau_1] = E[Y_1]$ となり、介入効果に関する良い推定量となります。

確率変数X,Y,Zで期待値をとる演算を$E_{XYZ}[f(X,Y,Z)]$と書きます。 $E_{XYZ} = \Sigma_x \Sigma_y \Sigma_z f(x,y,x) P(x, y, z)$です。$P(X,Y,Z) = P(Y|X,Z)P(X,Z)$ より、$E_{XYZ}[f] = E_{X,Z}[ E_{Y|XZ}[f] ]$が成り立ちます。

• $\hat{m}_1(X) = E[Y_1|X] $のとき

\begin{aligned}
E_{XYZ} [ \frac{Z-\hat{e}(X)}{\hat{e}(X)} ( Y_1 - \hat{m}_1(X) ) ] &= 
E_{XZ}[ E_{Y_1|XZ} \{ \frac{Z-\hat{e}(X)}{\hat{e}(X)}(Y_1 - \hat{m}_1(X)) \} ] \\
&=E_{XZ}[ \frac{Z-\hat{e}(X)}{\hat{e}(X)} \{ E_{Y_1|XZ}[Y_1] - \hat{m}_1(X) \}] \\
&=E_{XZ}[ E[Y_1|X] - E[Y_1|X] ] \\ &= 0
\end{aligned}

2行目から3行目では、強く無視できる割り当ての仮定より、$E_{Y_1|XZ}[Y_1] = E_{Y_1|X}[Y_1]$ を使っています。

• $\hat{e}(X) = P(Z=1|X)$ のとき

\begin{aligned}
E_{XYZ} [ \frac{Z-\hat{e}(X)}{\hat{e}} ( Y_1 - \hat{m}_1(X) ) ] &=
E_{X Y_1}[ E_{Z|X Y_{1}} \{  \frac{Z-\hat{e}(X)}{\hat{e}(X)}(Y_1 - \hat{m}_1(X))  \}  ] \\
&= E_{X Y_{1}} [  (Y_1 - \hat{m}_1(X)) E_{Z|X Y_1} \{ \frac{Z-\hat{e}(X)}{\hat{e}(X)} \} ] \\
&= E_{X Y_{1}} [  (Y_1 - \hat{m}_1(X)) \{ \frac{1}{\hat{e}(X)}E_{Z|X Y_1}(Z) - 1 \} \\
&= E_{X Y_{1}} [  (Y_1 - \hat{m}_1(X)) \{ \frac{\hat{e}(X)}{\hat{e}(X)} -1 \} \\
& = 0
\end{aligned}

3行目から4行目では、強く無視できる割り当ての仮定より、$E_{Z|XY}(Z) = E_{Z|X}(Z)$を使っています。

よって、 $\hat{m}_1(X) = E[Y_1|X]$ のとき、あるいは $\hat{e}(X) = P(Z=1|X)$ のときに

$E_{XYZ}[\tau_{1}] = E_{XYZ}[Y_{1}]$

が成り立ちます。