はじめに
データからどのようなグループがあるかを教師なしで分析する手法として、クラスタリング分析があります。k-meansなどのアルゴリズムが有名ですが、これは特徴量が量的(連続する数値)の時に使える手法です。実務においては、性別や職業などの質的なカテゴリー変数も含まれることが多く、この場合はk-meansなどをそのまま使うことは好ましくありません。このような量質混合データのときに、クラスタリングする手法について調べてみました。
手法を網羅的に調べた論文、記事は他にもあり、末尾の参考文献にも挙げています。本稿では、Pythonを使って実際にK-Prototypeによる分割クラスタリング、Gower距離を使った階層クラスタリングを実装して、結果を確認することに焦点を当てたいと思います。
Pythonコードの主要な部分はこの記事に記載しますが、スペースの都合ですべては掲載していません。すべてのコードはGithubにあげていますので、よろしければこちらをご参照ください。
本稿では、用語を以下のように使います。
- 量的データ:売上などの量的な特徴量だけを含むデータ
- 質的データ:性別、職業などの質的なカテゴリカルな特徴量だけを含むデータ
- 量質混合データ:上記の量的な特徴量と質的な特徴量の両方を含むデータ
量的特徴量でのクラスタリングについて(簡単におさらい)
カテゴリカル変数をクラスタリングで扱うかを見る前に、数値変数に対するクラスタリングの手法をおさらいしておきましょう。既にK-meansとか知っているよという人は読み飛ばしてください。
クラスタリングには大きく分けて分割クラスタリング(Partitional clustering)、階層クラスタリング(Hierarchical clustering)があります。
分割クラスタリングではK-means 、K-means++が有名です。scikit-learnではKMeansを使って実行できます。これは1つのデータを1つのクラスタに分類するので、ハードクラスタリングと呼ばれます。
分割クラスタリングでソフトクラスタリングであるものとして、Fuzzy C-means(FCM)があります。画像認識やマーケティングで使われることがあるようです。scikit-learnでは実行できず、scikit-fuzzyを入れると実行できるみたいです。
分割クラスタリングの欠点としては、クラスター数を予めしてしないといけないということです。クラスター数を決定する方法としては、エルボー法(Elbow method)があります。
階層クラスタリングはデンドログラムが描けるので、視覚的に理解したいときに便利です。また、クラスタ数を予め指定する必要がないというメリットもあります。
この記事で扱うデータ
低体重児のリスクファクターに関するケースコントロール研究のデータを使います。低体重児(出生体重2500g未満)発生要因として、母親の年齢、最終月経時の体重などを検討した研究で使用されたものです。(Hosmer and Lemeshow 1989)。これはロジスティック回帰などで要因、各特徴量とリスクの関係が研究されたデータですので、クラスタリング向きではないかもしれません。ですが、件数が189件と階層クラスタリングもデンドログラムで可視化できて、量的データと質的データが混じっているのでこのデータを使うことにしました。
ロジスティック回帰によるこのデータの解析は、「ロジスティック回帰分析: SASを利用した統計解析の実際」に記載されています。私の過去の記事でも、軽く扱っています。気になる方はご参考にしてください。
データの読み込みと前処理
データを読み込んで、量的なデータについては標準化を行っておきます。標準化しておかないと、特徴量のスケール自体に距離が影響されてしまい、クラスタリングが適切に行われないからです。
始めに、ライブラリをインポートします。後で使うクラスタリングのためのライブラリもここに含まれています。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 量的データの標準化
from sklearn.preprocessing import StandardScaler
# K-Prototypeクラスタリング
from kmodes.kprototypes import KPrototypes
# Gower距離
import gower
# 階層クラスタリング
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram
df0 = pd.read_csv('./rawdata/Low_Birth_Weight_Infants.csv')
df = df0[["MotherID"]].copy()
df.rename(columns={"MotherID":"ID"}, inplace=True)
df["low"] = df0["Low"]+0
df["age"] = df0["Age"].apply(lambda x:int(x[9:x.find(",")]))
df["lwt"] = df0["LWT"].apply(lambda x:int(x[9:x.find(",")]))
df["race"] = df0["Race"]
df["smoke"] = df0["Smoker"]
df["ptl"] = df0["PTL"]
df["ht"] = df0["Hypertension"]#高血圧歴
df["ui"] = df0["UI"]#+0
# カテゴリカル特徴量は文字型にしておく
df['race'] = df['race'].astype(str)
df['smoke'] = df['smoke'].astype(str)
df['ht'] = df['ht'].astype(str)
df['ui'] = df['ui'].astype(str)
ロジスティック回帰で使われる正解データである「label」、および「ID」はクラスタリングに使う特徴量から除きます。そして、標準化を実施します。
X = df.drop(columns=['low', 'ID'])
X_numerical = X[['age', 'lwt', 'ptl']]
X_categorical = X[['race', 'smoke', 'ht', 'ui']]
stdscl = StandardScaler()
X_numerical_scl = pd.DataFrame( stdscl.fit_transform(X_numerical) , columns=X_numerical.columns)
X_scl =pd.concat([X_numerical_scl, X_categorical], axis=1)
X_scl.head()
この標準化後のX_sclを使って、以下で2つのクラスタリング手法を実行します。
K-modes、K-Prototypeで分割クラスタリング
K-mode, K-Prototypeについて
Huangという方が提唱した、質的データ、量質混合データに対するクラスタリング手法です。クラスタリングするには、非類似度(dissimilarity)を測る距離を定義する必要があり、特徴量が量的ならばユークリッド距離を通常用います。
質的な特徴量に対して、この著者は以下のシンプルなマッチング非類似度(Simple matching dissimilarity)を用いることを提唱しています。
$X,Y$をm次元の質的特徴量だけから成るベクトルとし、その各成分を$x_j, y_j \quad (j=1, ... m)$とします。
$d_1(X,Y) = \sum^m_{j=1} \delta(x_j, y_j),$
$\delta(x_j, y_j) = 0 $ if $x_j = y_j, $
$ \hspace{20mm} = 1 $ if $ x_j \neq y_j$
量質混合データの場合を考えます。
$d_2(X,Y) = \sum^p_{j=1}(x_j - y_j)^2 + \gamma \sum^m_{j=p+1} \delta(x_j, y_j)$
右辺の第1項は量的データから計算されるユークリッド距離、第2項が質的データから計算されるマッチング非類似度です。第2項には係数 $\gamma$ が掛かっており、量的データと質的データの非類似度の重みを決めるパラメータです。
以下で使うK-modeのライブラリでは、何も指定しないと著者Huangが提唱している方法で$\gamma$は自動的にデータから計算されます。量的特徴量の分散$\sigma$をデータから求めてから$\gamma$を決定しており、参考資料[6]に議論されています。このパラメータ$\gamma$が入ってくるところがこのK-Prototypeを使う上で理解しておかないといけない点だと思います。
K-mode, K-prototypeのPythonでの実装
以下のコマンドで、kmodesをanadondaにインストールします。
$ conda install -c conda-forge kmodes
インストールしたら、以下のようにライブラリをインポートします。
# K-Prototypeクラスタリング
from kmodes.kprototypes import KPrototypes
K-Prototypeの引数に必要となる、質的変数のカラム位置を求めます。
catColumnsPos = [ X_scl.columns.get_loc(col) for col in list(X_scl.select_dtypes('object').columns) ]
catColumnsPos
KPrototypeライブラリを使ってクラスモデルを実行します。k-meansの時と同じように、エルボー法を用いてクラスター数を決めることにします。クラスタリングの当てはまりの良さを表す指標として、KPrototypeでは、属性.cost_を使います。(scikit learnのKMeansの時は属性.inertia_でしたので、注意が必要です。)
list_n_cluster = []
list_cost = []
for _n in tqdm.tqdm(range(1,16,1)):
try:
kprototype = KPrototypes(n_jobs = -1, n_clusters = _n, init = 'Huang', random_state = 0)
kprototype.fit_predict(X_scl, categorical = catColumnsPos)
list_n_cluster.append(_n)
list_cost.append(kprototype.cost_)
except:
break
plt.plot(list_n_cluster, list_cost)
plt.xlabel('n_cluster')
plt.ylabel('cost')
下図はクラスター数n_clusterとcostの関係をプロットしたグラフです。
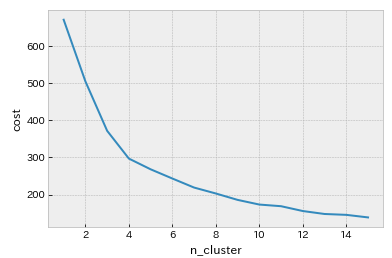
クラスター数が10くらいで、ようやくcostの減少が緩やかになっています。クラスター数を10として、クラスタリング結果を確認します。n_cluster = 10を指定してK-Prototypeを実行し、10分割された各クラスターに対して、量的データは平均値、質的データは最頻値(mode)を求めます。クラスタリングに用いた特徴量だけでなく、正解ラベルである「low」の平均値を求めて、各クラスターでpositive(低体重児)の割合も求めます。結果はこのlowの平均値でソートしておき、この順にラベルをlabel2として定義しておきます。(これは、次のGower距離による階層クラスタリングと結果を比較するときに使います)
kprototype = KPrototypes(n_jobs = -1, n_clusters = 10, init = 'Huang', random_state = 0)
kprototype.fit_predict(X_scl, categorical = catColumnsPos)
df_KProto = df[['ID', 'low']]
df_KProto = pd.concat([df_KProto, X], axis=1)
df_KProto['label'] = kprototype.labels_
df_KProto.head()
df_KProto_cluster = df_KProto.groupby('label').agg(
{
'label':'count',
'low': 'mean',
'age': 'mean',
'lwt': 'mean',
'race': lambda x: x.value_counts().index[0],
'smoke': lambda x: x.value_counts().index[0],
'ptl': 'mean',
'ht': lambda x: x.value_counts().index[0],
'ui': lambda x: x.value_counts().index[0]
}
).rename(columns={'label':'Count'}).reset_index()
df_KProto_cluster = df_KProto_cluster.sort_values('low').reset_index(drop=True)
df_KProto_cluster['label2'] = df_KProto_cluster.index
df_KProto_cluster
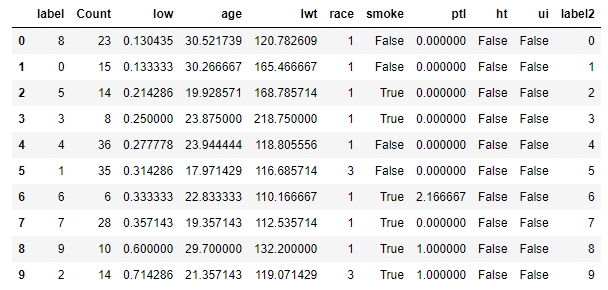
下に行くほど、つまり低体重児の割合が増えるほど、特徴量smokeの最頻値がTrue、すなわち喫煙になっています。
Gower距離行列で階層クラスタリング
Gower 距離について
Manhattan距離とDice距離を組み合わせて定義される距離です。
$S_{ij} = \frac{\sum_k^n w_{ijk} s_{ijk}}{\sum_k^n w_{ijk}}$
$k$は特徴量を表す添え字です。特徴量$k$が量的ならば
$s_{ijk} = |x_{ik} - x_{jk}| / R_k$, $R_k$は特徴量kがとる範囲(最大値-最小値)。分子はManhattan距離に相当しています。
$k$が質的ならば、$x_{ij} = x_{jk}$の時に1, $x_{ij} \neq x_{jk}$のときに0となります。これはDice dissimilarityと同じになります。
Gower距離を使ったクラスタリングのPython実装
PythonでGower距離を計算するためのライブラリ、その名も"gower"をインストールします。(調べたところ、pip install しかないようです。conda install できないのはanacondaユーザーとしては少し気持ち悪いですが、インストールしました)
pip install gower
次にライブラリをインポートします。
# Gower距離
import gower
標準化したデータに対して、各データ間のGower距離を求めて、行列として出力します。
X_distance = gower.gower_matrix(X_scl)
X_distance
この求めた距離を、scikit-learnの凝集型階層クラスタリングを実行するAgglomerativeClusteringに入れます。距離をすでに計算しているので、affinity='precomputed'を指定します。
AggCluster = AgglomerativeClustering(n_clusters=10, linkage='complete',
affinity='precomputed', compute_distances=True)
AggCluster.fit(X_distance)
デンドログラムを描かせると以下のようになります。
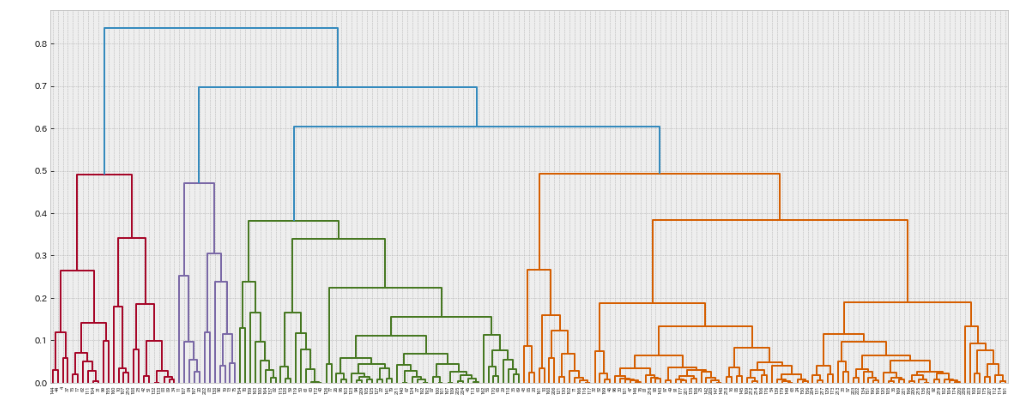
デンドログラムでそれなりに深さがある縦軸のcostが0.35あたりで見ると、クラスターは10個くらいに分割されそうです。ここでも分割数を10として、クラスターの予測ラベルを付与してみます。(本来、階層クラスタリングは予め分割数を指定する必要がないのがメリットの一つです。ただし、予測ラベルを付ける場合にはn_clusterを指定する必要があります。)
Gower距離を使った階層クラスタリングによる、各クラスターごとの平均値、最頻値をK-Prototypeの時と同様に確認します。
df_KAggCat = df[['ID', 'low']]
df_KAggCat = pd.concat([df_KAggCat, X], axis=1)
df_KAggCat['label'] = AggCluster.fit_predict(X_distance)
df_KAggCat.head()
df_KAggCat_cluster = df_KAggCat.groupby('label').agg(
{
'label':'count',
'low': 'mean',
'age': 'mean',
'lwt': 'mean',
'race': lambda x: x.value_counts().index[0],
'smoke': lambda x: x.value_counts().index[0],
'ptl': 'mean',
'ht': lambda x: x.value_counts().index[0],
'ui': lambda x: x.value_counts().index[0]
}
).rename(columns={'label':'Count'}).reset_index()
df_KAggCat_cluster = df_KAggCat_cluster.sort_values('low').reset_index(drop=True)
df_KAggCat_cluster['label2'] = df_KAggCat_cluster.index
df_KAggCat_cluster
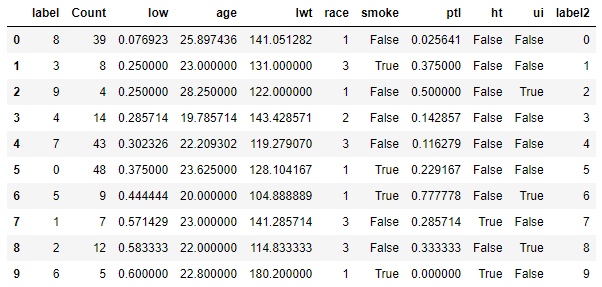
今回は、下に行くほど、すなわち低体重児の割合が高くなるクラスターでも、smokeがFalseであり喫煙していないクラスターがあります。ただし、下から3番目のクラスターでは、「ht」の最頻値がTrueすなわち高血圧歴ありになっています。先ほどのK-Prototypeによるクラスタリングとは別の観点でクラスター分けがなされているようです。
2手法のクラスタリング結果の比較
2つのクラスタリング手法を比較するため、低体重児の割合でソートしてラベルを付けた「label2」でクロス集計してみました。異なるロジックでクラスタリングしているので、あまり比較する意味はないかもしれませんが、2つのクラスタリング手法がどれくらい同じか/異なっているかを見る一つの目安として求めてみました。
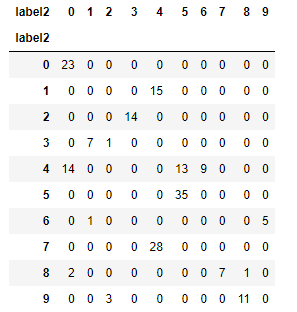
縦軸がK-Prototype、横軸がGower距離によるクラスタリング結果です。結構違っていますね。2つの手法でやってみて、データに即してどちらのクラスタリングがより解釈性が高いかを考察して選択することになりそうです。
最後に
今回は質量混合データに対する2つのクラスタリング手法を試しました。使っている距離も、クラスタリングのアルゴリズムも異なっているので、結果は2つの手法で結構違っていました。私がいずれ実務で使うときは、実際のデータを知悉した上で、結果を解釈して手法を選択することになると考えています。
なお、質的データに対する分析手法としては、他にも潜在クラスモデルを使う方法もあるようです。こちらのPython実装もやってみたいと思います。(Rなら簡単にできそうですが。。)
参考文献
[1]K-ModesClustering(Medium)
[2]Ahmad & Khan (2019) 量質混在データのクラスタリング手法レビュー
[3]The k-prototype as Clustering Algorithm for Mixed Data Type
[4]Clustering Categorical Data using Gower distance
[5]ZHEXUE HUANG, Extensions to the k-Means Algorithm for Clustering Large Data Sets with Categorical Values
[6]ZHEXUE HUANG, CLUSTERING LARGE DATA SETS WITH MIXED NUMERIC AND CATEGORICAL VALUES
[7]How to calculate Gower’s Distance using Python