Pythonのstatsmodelsで時系列データをトレンド、季節性、残差に分解する

はじめに

指標の時系列変化をプロットして確認するとき、原系列をそのまま示すのではなく、トレンドと季節性の成分に分解した結果も合わせて示すと理解が深まります。

このトレンドと季節性の分解する方法はいくつかありますが、ここでは、おそらく最もシンプルなものの一つであるstatsmodelsのseasonal_decomposeがやっていることを説明します。これは、移動平均でトレンド成分を求め、トレンド除去後のデータから周期成分を求めるというシンプルな方法です。

statsmodelsのドキュメントにもある通り、これはナイーブな分解方法なので、もっと洗練された方法を使ったほうがよい場面も多いと思います。しかし、これを理解しておくことは、ほかの洗練された方法の理解の出発点にもなるはずです。この記事が、中のロジックをよく見たことがなかった人への一助となればと思います。

#seasonal_decompose

seasonal_decomposeでは、以下のステップで時系列データをトレンド成分と季節成分に分解します。

1. 周期の長さで移動平均を求め、トレンド成分を求める
2. トレンド除去後の時系列から季節性の成分を求める
3. 残差を求める

seasonal_decomposeのソースを参考に、自分でコードを書いてみました。以下で詳しく見ていきます。

データ

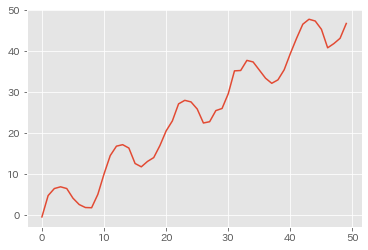
「トレンド＋正弦波＋正規分布のノイズ」で構成される時系列データを作ります。時系列全体の長さは50、周期は10とします。

# 季節性の周期は10
period = 10

#線形トレンド＋正弦波＋正規分布ノイズ
np.random.seed(seed=20210)
x_ts = [i + 5*np.sin(2*np.pi*i/period) + np.random.randn() for i in range(period*5)]
plt.plot(x_ts)

移動平均でトレンド成分を求める

移動平均を求めます。移動平均には

• 中央移動平均：各時点とその前後の時点の平均値を使う
• 後方移動平均：各時点とそれ以前の時点の平均値を使う

などがありますが、この記事では中央移動平均だけを扱います。

中央移動平均では、周期が偶数の時は注意が必要です。ある時点$i$の移動平均を求めるとき、この時点$i$の前後から周期-1個のデータを含めて平均する必要があります。周期が偶数の時、周期-1は奇数となり、そのままでは前と後ろで等分できません。そこで、前と後でそれぞれ周期/2個のデータをとり、ただし両端のデータの重みは$0.5$として移動平均をとります。

#両端のウェイトを0.5とする
filt = np.array( [.5] + [1]*(period-1) + [.5] )/period
print(filt)

# 移動平均を求め、トレンド成分を求める
x_trend = []
for _i in range(len(x_ts)):
    #print(_i)
    if _i <= int(period/2)-1 or _i >=len(x_ts) - int(period/2):
        x_trend.append(np.nan)
    else:
        _trend = 0
        for _j in range(len(filt)):
            #print(_i,_j)
            _trend += x_ts[_i-int(period/2)+_j]*filt[_j]
        x_trend.append(_trend)
        
x_trend = np.array(x_trend)
x_trend

季節成分を求める

まず、原系列から上で求めたトレンド成分を引き、トレンド除去の時系列データを求めます。
このトレンド除去後のデータから、周期ごとの平均値を求めます。（今の例だと、0,10,20,30,40時点の平均、1,11,21,31,41時点の平均・・）。ただし、周期成分の平均値は0となるように、全体の水準を設定します。

x_detrend = x_ts - x_trend
#周期ごとの平均を求める。欠損は無視して平均を求める。
x_period_average = [ np.nanmean(x_detrend[i::period]) for i in range(period) ]
#季節成分の平均は0となるようにする
x_period_average -= np.mean(x_period_average, axis=0)

残差を求める

残差は原系列からトレンド成分、季節性の成分を引くことで求まります。

#残差
x_resid = x_ts - x_trend - x_seasonal
x_resid

seasonal_decomposeを使う

上で少々長くコードを書きましたが、statsmodels.tsaのseasonal_decomposeを使うと

from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(x_ts, period=period, two_sided=True)

の２行で済みます。結果はresult.trend、result.seasonal、result.residからそれぞれトレンド成分、季節性の成分、残差を取り出せます。

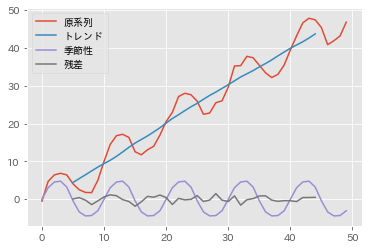
各成分に分解したプロットは以下のようになります。

移動平均を使っているため、両端には欠損が発生し、開始時点と終了時点ではトレンド成分と残差成分を描くことができません。これは、ナイーブな移動平均をつかう分解方法のデメリットの一つでしょう。ただし、何をやっているか非常にわかりやすいので、まず簡単に時系列データの傾向を確認するときなどには十分使えると思います。
洗練された手法としては、有名なSTL分解などがあります。この方法をpythonで実装する記事はいくつかありますので、興味ある方はご参照ください。