はじめに
動機
仕事でロジスティック回帰を久しぶりに実施することになりました。
この仕事では、単に精度がよい分類モデルを作るのではなく、係数の有意性などを確認し、分類に本当に効いている変数は何かを確認する必要があります。
仕事では、私だけでなくメンバーもpythonを使うことが多いので、できるだけPythonを使いたいです。ただし、一番メジャーな?scikit-learnだとパラメータのp値などは出力してくれません。そこで、Pythonのstatsmodelsライブラリを使うことにします。(これでできなさそうなら、Rを使うという方針でやりましたが、今回の範囲ではRが必要とはなりませんでした)。
この記事の内容
最終目標は、実際の「低体重児のリスクファクターに関するケースコントロール研究」データを使って、ロジスティック回帰により低体重児の発生要因を検討することです。この検討を理解するためには、「交絡因子」や「交互作用」といった用語を理解しておく必要があります。この記事では、私が生成した人工的なデータを用いてロジスティック回帰を用いた交絡因子、交互作用の検討を行います。記事が長くなるため、低体重児の発生要因は次の記事(執筆中)に譲ります。
この記事では、ロジスティック回帰を知っていることを前提とします。ロジスティック回帰で分類するモデルを作ることはだいだいわかっているが、ロジスティック回帰を使って交絡因子などを検討する方法はよく知らない読者を想定しています。ロジスティック回帰自体の説明は、ほかによい記事がありますので、そちらを参照していただきたいです。
なお、この記事ではロジスティック回帰に主眼を置いています。交絡因子などの検討は他の統計的手法もありますが、筆者が浅学なこともありここでは取り上げません。
この記事のコードとデータはGitHubに置いています。
コード
データ
pythonでロジスティック回帰を実施する
Pythonで分類モデルなどを作るとき、よく使われるライブラリーは scikit-learn だと思います。このscikit-learnに用意されているsklearn.linear_model.LogisticRegressionでは、係数の有意性を示すp値などが出力されません。精度が高い分類モデルを作るのが目的の場合はこれでよいのですが、発生要因を検討する目的では十分ではありません。
Pythonには statsmodels という統計モデルのライブラリがあり、これだとp値などを出力してくれます。このライブラリーの Generalized Linear Models を使うと、ロジスティック回帰を実施できます。
具体的には、以下のようなコードを書きます。
import statsmodels.api as sm
logit = sm.GLM(y, X, family=sm.families.Binomial())
logit_result = logit.fit()
print( logit_result.summary() )
sm.GLM で一般線形化モデルを呼び出し、引数familyに sm.families.Binomial() を指定するとロジスティック回帰モデルを実行します。fit() メソッドでパラメータ推定を実施し、result_summary() メソッドで推定結果を出力します。
交絡因子
ある因子(飲酒など)と結果(肺がん)の関係を考えるときに、その因子に付随し表に現れていないその他の因子が直接結果に影響して、注目している因子は直接的には関係ないことがあります。この表に現れていないその他の因子を交絡因子といいます。
飲酒と肺がんの発生有無の関係を調べると、飲酒する人の肺がん発生率が高いそうです。ただし、飲酒する人は喫煙する人も多いためこのような結果になります。結果である肺がんに直接影響を与えているのは喫煙であり、ここでは喫煙が交絡因子になります。
私が作ったサンプルデータで、肺がん、飲酒、喫煙の関係がロジスティック回帰でどのようになるかを見てみます(あくまでもこの例のために作ったサンプルデータで、実際の調査結果ではありません)。データはこちらに置いています。
| 肺がん発生 | 肺がんなし | |
|---|---|---|
| 飲酒あり | 102 | 239 |
| 飲酒なし | 52 | 244 |
飲酒なしと比較して、飲酒ありの対数オッズ比は$\ln((102/239)/(52/244)) = 0.69$ となります。
飲酒有無だけを説明変数とする単変数のロジスティック回帰モデルを求めると、次のようになります。
# サンプルデータの読み込み
df_conf = pd.read_csv('./data/sample_data_confounding.csv')
# 切片用のカラムを追加
df_conf["intercept"] = 1
# 単変数ロジスティック回帰
X = df_conf[ ['intercept', 'alcohol'] ]
y = df_conf['cancer']
logit = sm.GLM(y, X, family=sm.families.Binomial())
logit_result = logit.fit()
print( logit_result.summary() )
結果は以下のようになりました。
| 係数 | p値 | |
|---|---|---|
| 切片 | -1.5459 | 0.000 |
| 飲酒有無 | 0.6944 | 0.000 |
飲酒に有意な係数がつき、その値は上の対数オッズ比とほぼ一致しています。
このデータを喫煙あり、喫煙なしの層別に分けてみてみます。
- 喫煙あり
| 肺がん発生 | 肺がんなし | |
|---|---|---|
| 飲酒あり | 82 | 141 |
| 飲酒なし | 22 | 47 |
この層の対数オッズ比は$\ln((82/141)/(22/47))=0.22$です。
- 喫煙なし
| 肺がん発生 | 肺がんなし | |
|---|---|---|
| 飲酒あり | 20 | 98 |
| 飲酒なし | 30 | 197 |
この層の対数オッズ比は$\ln((20/98)/(30/197))=0.29$です。
喫煙あり/なしの層別にみると、飲酒の有無と肺がん発生の関係は弱くなっています。
今度は、飲酒有無と喫煙有無の2変数を説明変数とするロジスティック回帰モデルを求めてみます。
# 2変数ロジスティック回帰モデル(喫煙有無による調整)
X = df_conf[ ['intercept', 'alcohol', 'smoking'] ]
y = df_conf['cancer']
logit = sm.GLM(y, X, family=sm.families.Binomial())
logit_result = logit.fit()
print( logit_result.summary() )
結果は以下のようになりました。
| 係数 | p値 | |
|---|---|---|
| 切片 | -1.8664 | 0.000 |
| 飲酒有無 | 0.2524 | 0.241 |
| 喫煙有無 | 1.0799 | 0.000 |
喫煙有無による調整を入れたことで、飲酒有無の係数が0.6944から0.2524に大きく変化しています。さらに、今度はp値が0.242となっており、有意な結果ではありません。交絡因子がある場合は、交絡因子を入れてロジスティック回帰モデルを作ると、このように係数が大きく変わります。
交互作用
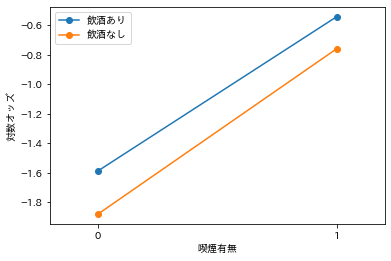
このデータでは(現実とはたぶん違っていると思います)、飲酒有無と喫煙有無の間には交互作用がないデータとなっています。飲酒ありと飲酒なしの対数オッズを、喫煙の有無でも区分してプロットしてみます。
飲酒ありと飲酒なしの対数オッズ自体は喫煙の有無で異なっています。ただし、飲酒ありと飲酒なしの対数オッズの差は、喫煙あり、喫煙なしでもほぼ同じとなっています。喫煙有無と飲酒有無が組み合わさって、効果が出ているという風にはなっていません。(これはあくまでの説明用の人工的なデータです。実際には、飲酒と喫煙の間に相互作用があることが報告されている論文もありますのでご注意ください)
これを簡単に数式で見てみましょう。飲酒有無 $x_1 = 0,1$ と喫煙有無 $x_2 = 0,1$ の2変数からなるロジスティック回帰モデル $\frac{1}{1+\exp(-\beta_1 x_1 - \beta_2 x_2)}$ を考えています。飲酒なし、喫煙なしを基準にした時の対数オッズ比は以下のようになります。
| 喫煙あり | 喫煙なし | |
|---|---|---|
| 飲酒あり | $\beta_1 + \beta_2 = 1.34$ | $\beta_1 = 0.29$ |
| 飲酒なし | $\beta_2 = 1.12$ | 0 |
$\beta_1$ と $\beta_2$の2パラメータで、3つの対数オッズ比をフィットしています。$\beta_1=0.29$と$\beta_2=1.12$を代入すると$\beta_1 + \beta_2 = 1.41$となりますが、これは実際の飲酒あり・喫煙あり対数オッズ比1.34に近い値です。この2パラメータでのフィットはよくいっており、交互作用項は必要ありません。
癌の発生有無には、遺伝的な要因も影響していると報告されています。そこで、特定の遺伝子を持つ人を1とする変数を加えてみます。
| 喫煙有無 | 特定DNA有無 | 肺がん発生 | 肺がんなし |
|---|---|---|---|
| あり | あり | 94 | 96 |
| なし | 10 | 92 | |
| なし | あり | 35 | 155 |
| あり | 15 | 140 |
このとき対数オッズは以下のようになります。
喫煙ありと喫煙なしの対数オッズの差が、特定DNAの有無によって大きく違っています。このように、喫煙有無と特定DNA有無が組み合わさって影響がでているとき、交互作用があるといいます。
先ほどと同じように、数式を使ってみます。遺伝子有無 $x_1 = 0,1$ と喫煙有無 $x_2 = 0,1$とします。
| 喫煙あり | 喫煙なし | |
|---|---|---|
| 遺伝子あり | $\beta_1 + \beta_2 = 2.21$ | $\beta_1 = 0.75$ |
| 遺伝子なし | $\beta_2 = 0.01$ | 0 |
2つのパラメータ$\beta_1$と$\beta_2$の2つでは、3つの対数オッズ比をうまくフィットできません。交互作用項を入れて、新たなパラメータ$\beta_{相互作用}$を入れると、モデルへのフィットが高まると期待されます。
まず比較対象として、喫煙有無だけを変数としたロジスティック回帰モデルを作ってみます。
X = df_conf[ ['intercept', 'smoking'] ]
y = df_conf['cancer']
logit = sm.GLM(y, X, family=sm.families.Binomial())
logit_result = logit.fit()
print( logit_result.summary() )
| 係数 | p値 | |
|---|---|---|
| 切片 | -1.7750 | 0.000 |
| 喫煙有無 | 1.1829 | 0.000 |
モデルの当てはまりを表す統計量の一つである対数尤度は 対数尤度 = -332.91 でした。
次に交互作用項を入れて実施します。
df_conf['smoking*DNA'] = df_conf['smoking'] * df_conf['DNA']
X = df_conf[ ['intercept', 'smoking', 'smoking*DNA'] ]
y = df_conf['cancer']
logit = sm.GLM(y, X, family=sm.families.Binomial())
logit_result = logit.fit()
print( logit_result.summary() )
| 係数 | p値 | |
|---|---|---|
| 切片 | -1.7750 | 0.000 |
| 喫煙有無 | -0.4443 | 0.225 |
| 喫煙有無×遺伝子 | 2.1982 | 0.000 |
交互作用項を入れると対数尤度 = -307.17 となり、交互作用項を入れない時よりも当てはまりはよくなっています。
このように、2つの変数の組み合わせで対数オッズの差を確認し、交互作用の影響が確認される場合は、交互作用項をモデルに入れたほうがよいです。