Simulinkで離散時間MRAC

はじめに

昨年末，連続時間におけるモデル規範適応制御(MRAC, Model Reference Adaptive Control)について記事を書きました。
Simulinkで始める線形システムのモデル規範適応制御(MRAC)

「適応制御を導入すれば，制御対象の特性がある程度変化してもリアルタイムにパラメータ調整して制御特性を一定に保てる」という趣旨の記事でしたが，その制御則は連続時間で立てられたものでした。

しかし，マイコンなどのデジタルなプロセッサを使って制御をかける場合，実現されるのは連続時間制御ではなく離散時間制御になります。もちろん離散時間で連続時間制御の処理を疑似的に再現するアプローチもありですが，制御周波数が制御対象の動作に比べて遅い(粗い)と狙い通りの性能は出せません。完全に連続時間のふるまいを模擬できる離散化手法はありませんし，離散時間には離散時間なりの制御理論が存在します。

そこで今回は離散時間モデル規範適応制御(MRAC)をSimulinkで実装してみました。
前回と同様，「理論はさておきまずは動くものを」というスタンスで行きます。

なお，本記事では離散制御における時間変数を $t$ではなく$k$で表します。
また，$ z^{-n} $は$n$ステップ遅延を表す演算子です。例えば $z^{-2}x(k)$は$x(k-2)$のことです。
num, denという名を冠したMatlab変数が度々出てきますが，それぞれ伝達関数の分子係数，分母係数のことだと思ってください。

ツールは以下のものを使っています。

• Matlab 2021b
• Simulink
• Control System Toolbox

Simulinkで離散時間MRAC

線形システムをMRACで制御するモデルをSimulink上で構成しました。

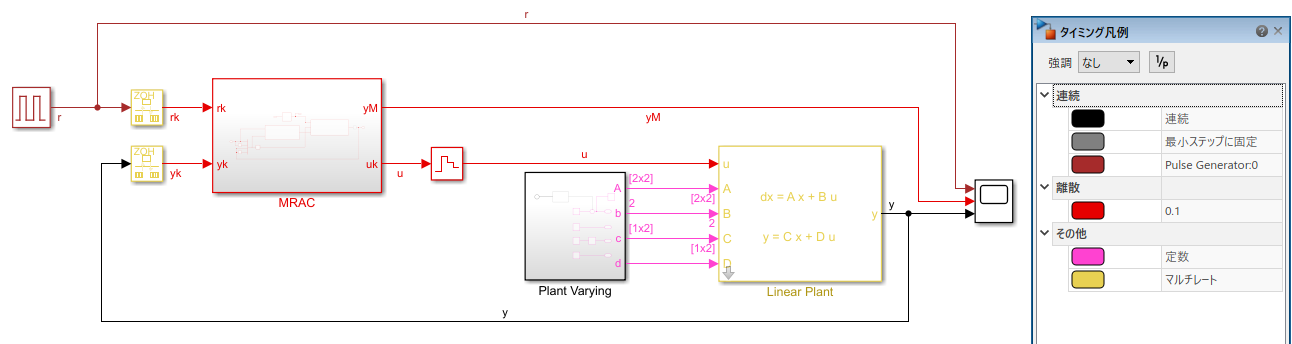
ただし離散時間制御なので，制御器の入力にはサンプラーとしてレート変換ブロックを，出力にはゼロ時ホールドブロックを挟んでいます。(無くてもゼロ時ホールド出力になるけど。) 赤枠，赤線が離散時間で動作する部分です。

大きく，制御対象(Linear Plant)とその状態方程式の係数を変動させるブロック(Plant Varying)，そして適応制御ブロック(MRAC)に分かれています。(今回Plant Varyingブロックには定数のみを出力させます)

前回はオブザーバ(MRACでは状態フィルタ)を省略して状態$\boldsymbol{x}$を直接取得していましたが，今回は出力$y$のみを取得しています。離散時間でのMRACではオブザーバ的なものを使わず，制御入力$u(k)$と制御出力$y(k)$の過去の系列のみを用いて制御をするためです。潔くて良いですね。

制御対象

下記の状態方程式とパラメータで表される制御対象を扱います。前回と同様，倒立振り子のように自由応答が不安定なタイプの制御対象です。

\begin{align}
\dot{\boldsymbol{x}}(t) &= A \boldsymbol{x}(t) + \boldsymbol{b} u(t) \\
y(t) &= \boldsymbol{c}^\top \boldsymbol{x}(t)
\end{align}

A = [0, 1; -2, 3];
b = [0; 1];
c = [1; 0];

適応制御器

適応制御ブロックの中身を示します。

基本構造

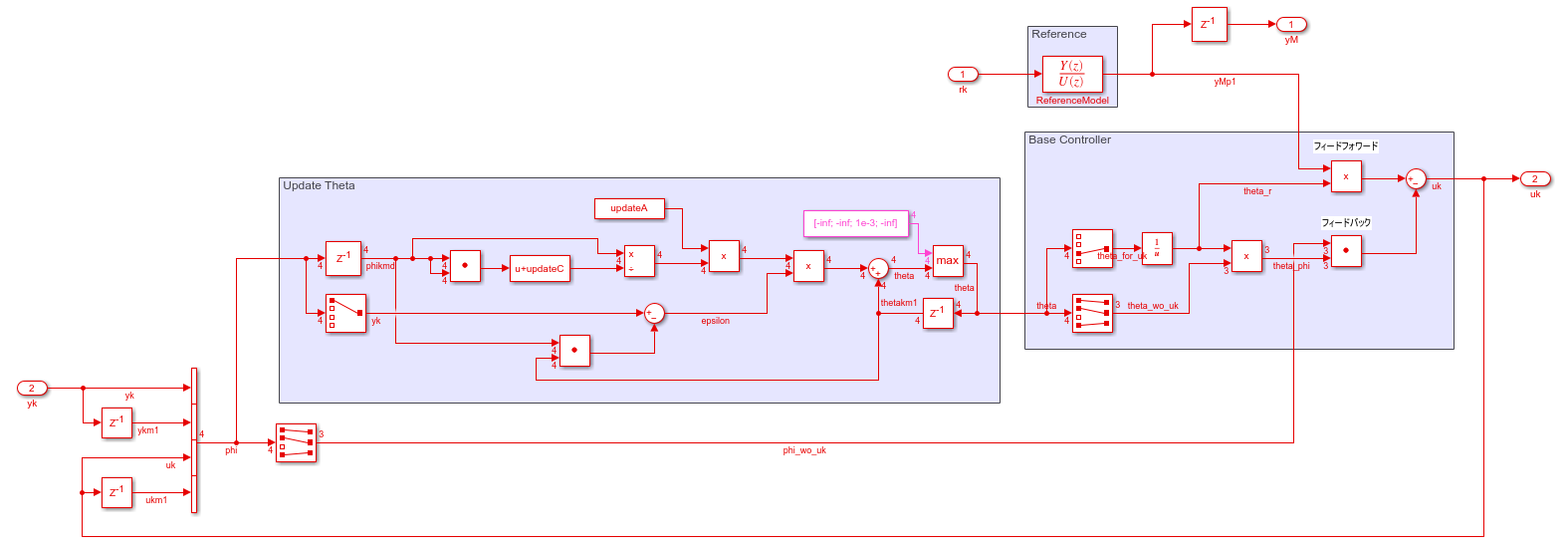
連続時間の場合と同様，規範モデル(Reference)，ベースとなる制御部(Base Controller)，制御パラメータ更新部(Update Theta)に分かれています。

規範モデルは，制御目標値$r(k)$に対する理想的な応答$y_M(k)$を作るモデルです。参照モデル自体は離散時間伝達関数で表されています。

ベースとなる制御は，大雑把にフィードバック＋フィードフォワード制御を構成していますが，前回の連続時間の場合と入力情報がすこし異なります。前回は，パラメータ$\boldsymbol{\theta}(t)=[\theta_r(t),\boldsymbol{\theta_x}(t)^\top]^\top$と，目標値と状態をまとめたベクトル$\boldsymbol{\omega}(t)=[r(t),\boldsymbol{x}(t)^\top]^\top$の内積でフィードフォワード＋フィードバック制御を構成していました。今回はフィードフォワードにおいて目標値$r(t)$の代わりに規範応答$y_M(k)$を，フィードバックにおいて$\boldsymbol{\omega}(t)$の代わりに$\boldsymbol{\phi}(k)=[y(k), y(k-1), u(k), u(k-1)]^\top$を用いています。ただし，制御入力$u(k)$を決めるのに$u(k)$を使うことはできないので(Simulinkだと代数ループが発生しますね)，$u(k)$だけベクトルから取り除いて使っています。
今回は時刻$k, k-1$の情報だけ用いていますが，この用いる系列の長さは制御対象の離散時間伝達関数(後述)の次数で決まります。

パラメータ更新部では制御パラメータ$\boldsymbol{\theta}(k)$を適応的に調整します。パラメータの更新の目的は，規範応答$y_M(k)$と実際の応答$y(k)$の誤差$e(k)=y_M(k)−y(k)$を$0$にすることです。

制御対象の離散時間表現

各構成要素の説明の前に，今回の制御設計に用いる制御対象の離散時間表現について説明しておきます。

制御対象は離散時間伝達関数

G(z^{-1}) = z^{-d} \frac{N_p(z^{-1})}{D_p(z^{-1})} = z^{-d} \frac{b_0 + b_1 z^{-1}+\cdots + b_m z^{-m}}{1 + a_1 z^{-1}+\cdots + a_n z^{-n}}

の形で表現します。分母次数は$n$，分子次数は$m$です。$z^{-d}$は$d$ステップの遅延です。

伝達関数表現は下記の項目を守る必要があります。

• $d \geq 1$
  • 参考文献には特に記述ありませんでしたが，$d \geq 1$でないと代数ループが発生します。
• $b_0 \neq 0$
  • もし$b_0 = 0$となってしまったときは，$z^{-1}$をくくって遅延$z^{-d}$に含ませることができます。
• 零点は単位円内$|z|<1$に存在
  • 適応制御の漸近収束性を保証するためです。極ではなく零点です。

今回の制御対象について上記の離散時間表現してみましょう。ただしサンプリング周期は$T_s = 0.1\ \mathrm{s}$とします。

まずは状態方程式表現されている制御対象を連続時間伝達関数で表現します。

%% 制御対象のパラメータの推定値(=真値のとき)
AHat = A;
bHat = b;
cHat = c;

[num, den] = ss2tf(AHat,bHat,cHat',0);
plantHat = tf(num, den)

plantHat =
 
        1
  -------------
  s^2 + 3 s - 2
 
連続時間の伝達関数です。

これをc2dコマンドで離散化します。離散化手法はzoh変換を選びます。
(「tustin変換などで得られる周波数特性の一致性よりも，時間応答の一致性が欲しいから」というのもありますが，tustinを含め離散化方法によっては上記の離散時間表現の要件を満たさないからです。)

%% 制御対象離散化
Ts = 1e-1; 
plantDisc = c2d(plantHat, Ts, 'zoh');
[plantDiscNum, plantDiscDen] = tfdata(plantDisc, 'v');
plantDisc = filt(plantDiscNum, plantDiscDen, Ts) % これではb0=0となってしまう。

plantDisc =
 
  0.004543 z^-1 + 0.004111 z^-2
  -----------------------------
  1 - 1.758 z^-1 + 0.7408 z^-2
 
サンプル時間:  0.1 seconds
離散時間の伝達関数です。

分子の定数項$b_0$が$0$になってしまいましたね。$d=1$の遅延$z^{-1}$があるということなので取り出しましょう。

%% b0=0は許容されないので遅延z^-1を取り出す
plantDiscNum = plantDiscNum(2:end);
plantDisc = filt(plantDiscNum, plantDiscDen, Ts)

d = 1; % 遅延 z^-d = z^-1

plantDisc =
 
    0.004543 + 0.004111 z^-1
  ----------------------------
  1 - 1.758 z^-1 + 0.7408 z^-2
 
サンプル時間:  0.1 seconds
離散時間の伝達関数です。

$d \geq 1, b_0 \neq 0$の離散時間伝達関数で表すことができました。

零点も単位円内にあるので問題なさそうです。

zero(plantDisc)

ans =

         0
   -0.9050

ギリギリですけど。

ベースとなる制御

ベースとなる制御は，規範応答$y_M(k)$とパラメータ$\boldsymbol{\theta}=[\theta_1, \theta_2, \theta_3, \theta_4]^\top$，そしてフィードバック値$\boldsymbol{\phi}(k)=[y(k), y(k-1), u(k), u(k-1)]^\top$の各要素を用いて，

u(k) = \frac{1}{\theta_3}\{y_M(k+d)-\theta_1 y(k) -\theta_2 y(k-1) -\theta_4 u(k-1)\}

としています。ごちゃごちゃしているように見えますが，

y_M(k+d) = \boldsymbol{\theta}^\top \boldsymbol{\phi}(k)

を$u(k)$について解いたものです。
分母の$\theta_3$が$0$に近づくのは怖いので，パラメータ更新部で$0.001$以上になるようにしています。

$y(k)$の過去値は$y(k-n+1)$まで，$u(k)$の過去値は$u(k-m-d+1)$まで使います。今回$n=2, m=1, d=1$なので$y(k-1), u(k-1)$まで使うことにします。

ところで$y_M(k+d)$を使うとすると，規範応答$y_M(k)$の$ d $ステップ未来の値が必要になってしまいます。
目標値$r(k)$が事前に決まっているなら問題なく未来値を適用すれば大丈夫です。
そうでない場合は次節のように規範モデルを上手く設定して未来値の使用を避けます。

規範モデル設計

前回の連続時間の規範モデルをそのまま離散化したものを用います。

% 規範モデル
deltaM = 0.8; % ちょっとだけオーバーシュート
omegaNM = 7.5; % ±2%正定時間が0.5s程度
WsNum = [1/omegaNM^2, 2*deltaM/omegaNM, 1]; % それぞれ s^2, s, 1の係数
refTF = tf(1, WsNum);
refDisc = c2d(refTF, Ts, 'zoh')

refDisc =
 
     0.1875 z + 0.1253
  -----------------------
  z^2 - 0.9884 z + 0.3012
 
サンプル時間:  0.1 seconds
離散時間の伝達関数です。

$z$ではなく$z^{-1}$についての式にするために分子と分母に$z^{-2}$をかけると，分子の定数項が消えて遅延$z^{-1}$が現れると思います。
今回$d=1$であり，ベースとなる制御で$y_M(k)$の1ステップ未来値$y_M(k+1)$が必要でしたが，この遅延成分で打ち消せるので問題なしです。

規範モデルに$z$を1個かけて，堂々と未来値$y_M(k+1)$を使ってやりましょう

[refDiscNum, refDiscDen] = tfdata(refDisc, 'v');
refDiscNum = [refDiscNum(2:end), 0]; % +d分未来の値を用いる(分子にzをかける)

適応則設計

適応則は

\boldsymbol{\theta}(k) = \boldsymbol{\theta}(k-1) + a(k) \frac{\boldsymbol{\phi}(k-d)}{c + \boldsymbol{\phi}(k-d)^\top\boldsymbol{\phi}(k-d)} \epsilon(k)

としています。(※ $c$は制御対象の状態方程式の$\boldsymbol{c}$とは異なります)
$ 0 < a(k) < 2, c > 0$です。この係数に応じた適応の傾向は私自身まだわかっていませんが，$a(k)=0$だと$\boldsymbol{\theta}(k)$がまったく更新されないことになります。

$\epsilon(k)$は

\epsilon(k) = y(k) - \boldsymbol{\theta}(k-1)^\top \phi(k-d)

です。

ここでネタバラシをすると，制御パラメータ$\boldsymbol{\theta}$はただの制御パラメータではなく，$y(k)$の$d$ステップ先の未来値を予測する，$d$ステップ予測器

y(k+d) = \boldsymbol{\theta}^\top \phi(k)

のパラメータだったのです。$\epsilon(k)$はその予測誤差ということになります。

この離散時間MRACは未来値$y(k+d)$を規範モデル応答$y_M(k+d)$に沿わせることを目標としています。予測器のパラメータが完璧なら，

y(k+d) = \boldsymbol{\theta}^\top \phi(k) = y_M(k+d)

となるように$u(k)$を決めれば目標が達成できるようになります。(そうしてできたのが，前述した「ベースとなる制御」です。)

そして予測器が完璧でない場合に，予測誤差$\epsilon(k)$に基づいて$\boldsymbol{\theta}$に修正をかけるのが適応則というわけです。

制御パラメータの解

ところで「完璧な予測パラメータ」があったとすれば，それはすなわち$y(k) = y_M(k)$を実現する制御パラメータということになりますが，それはどのように導出するのでしょうか？

まず$d$ステップ予測器を

\begin{align}
y(k+d) &=& \alpha(z^{-1})y(k) + \beta(z^{-1})u(k)\\
&=& (\alpha_0 + \alpha_1 z^{-1} + \cdots + \alpha_{n-1}z^{-(n-1)})y(k)\\
&& + (\beta_0 + \beta_1 z^{-1} + \cdots + \beta_{n-1}z^{-(n+d-1)})u(k)
\end{align}

とします。$\boldsymbol{\theta}$の中の$y(k), y(k-1), \cdots$に関する係数を$\alpha$，$y(k), y(k-1), \cdots$に関する係数を$\beta$としています。

次に離散時間プラントモデルが既知として，
Diophantine方程式

F(z^{-1}) D_p(z^{-1}) + z^{-d}G(z^{-1})=1\\
F(z^{-1}) = f_0 + f_1 z^{-1} + \cdots + f_{d-1}z^{-(d-1)}\\
G(z^{-1}) = g_0 + g_1 z^{-1} + \cdots + g_{n-1}z^{-(n-1)}

を$F(z^{-1}), G(z^{-1})$について解きます。係数比較で一意に解が出ます。

この解を使って

\alpha(z^{-1}) = G(z^{-1}) \\
\beta(z^{-1}) = F(z^{-1}) N_p(z^{-1})

とすれば，予測器，すなわち制御パラメータ$\boldsymbol{\theta}$の完成です。

今回はこの値を制御パラメータの初期値とします。

initialTheta = [-plantDiscDen(2); -plantDiscDen(3); plantDiscNum(1); plantDiscNum(2)]; % Diophantine方程式から導出

制御結果

制御対象モデルに誤差があったときの適応制御の動きを確認してみましょう。

真の制御対象のパラメータ

A = [0, 1; 2, -3];
b = [0; 1];
c = [1; 0];

に対し，行列$A$の2行1列成分に$-1$を，2行2列成分に$0.5$をかけた

AHat = A .* [1, 1; -1, 0.5];
bHat = b;
cHat = c;

というパラメータについて制御パラメータを合わせこんでしまった状態から制御を開始してみます。

倒立振り子で例えるなら，重力の向きを逆向きにし，粘性抵抗も半分という想定でモデルを作ってしまい，「放っておけば勝手に倒立するよね！？」という認識で制御設計してしまったような状況です。(そんなことある？)

目標値$r(k)$を2秒おきに1→0→1→0...とステップ上に変化させて与えてみます。

適応制御なし

適応制御なしで「完璧なパラメータ(勘違い)」によって制御したときの動作です。

黄色線(r)が目標値，青線(yM)が規範応答(離散時間)，赤線(y)が実際の応答です。

目標値付近にて徐々に振幅が大きくなり，発散してしまいました。

適応制御あり

離散時間MRACを導入してみましょう。

適応パラメータは次のように設定します。

% 適応パラメータ
updateA = 1.0; % 0 < a < 2
updateC = 1.0; % c > 0

(約1分30秒あります)

突然発散したたかと思いきや，その後も一応不安定にならず規範応答に追従する様子が分かります。しかし規範モデルに沿っては離れ，沿っては離れ，ときどき大きな振幅で揺れてしまう場合もあり，正直心許ない応答ですね。適応制御が効いていなかったときのように発散したわけではないのでそこは一歩前進ですが…

この適応制御をずっと放っておくとどうなるのでしょう。ペーシング(リアルタイム再生)を切って早送りしてみます。

およそ2000秒，制御500回分で規範モデルに収束している様子が見えます。

理論上は$e(k)\rightarrow 0\ (k \rightarrow \infty)$が保証されているので，確かに最後には規範モデルに追従する様子を見せてくれました。しかし適応途中の応答についてはせいぜい有界であることしか保証されていないので，場合によっては一見不安定なレベルの応答を見せることもあるのでしょう。

ちなみに，適応パラメータ$a$と$c$を様々に振ってみましたが，適応に至るまでの過渡応答の悪さは改善しませんでした。

おわりに

今回の適応制御導入で得られた結果は，「最終的に適応($ y(k)=y_M(k) $の実現)はしてくれたけど，適応するまでの途中の応答の悪さは見過ごせないよね。」というものでした。もちろん，その良し悪しはアプリケーションによりますが。

取りうる対策としては

• 適応を高速化して応答が悪くなる余地を与えない
• 応答が悪くならない (たとえば誤差$ e(k) $が大きくなりすぎない) 範囲で適応させる

というのが考えられると思います。

本記事で紹介した適応則は，ごくごく基本的なものの一例であり，過渡応答を改善する工夫はこれまで数多く研究されているようです。(適応制御の研究の起こり自体1960年代ですし…)

例えば，今回採用した適応則は，参考文献『適応制御』における「適応則Ⅰ」に相当するものですが，「適応則Ⅲ 最小2乗型」のようにパラメータがより早く収束する適応則も紹介されています。多少アルゴは複雑になりますが，採用することで対策案の1つ目が実現できるかもしれません。もう少し調査が必要ですね。

参考文献

• 宮里 義彦. "適応制御." コロナ社 (2018).