はじめに
制御設計においては,制御対象をモデリングをする際に,伝達関数式や状態方程式のような数理モデルに落とし込むことがほとんどだと思います。Matlabコマンドでいえば,tfやssで作れるあのモデルオブジェクトに相当するものです。
これらの数理モデルは物理法則から立式することもあれば(第一原理モデル),測定データを使ってシステム同定をかけて得ることもあるでしょう。
一方で,制御対象の数理モデルを立てずに測定データをそのまま使って制御設計するというモデルフリーなやり方もあると思います1。
周波数応答データに基づいて制御設計するなら,「周波数応答データ (FRD) モデル」で表現すると便利です。(モデルなんだかデータなんだか)
frdというコマンドで生成できます。
ただ,状態空間モデルを作るssや伝達関数モデルを作るtfに比べると,あまり使われていない(知られていない?)印象があります。
「matlab tf」でQiitaの記事を検索すれば145件出るのに,
「matlab frd」で検索するとこの記事を含めて2件しかありません。
Matlab 2006aより前からある由緒正しきコマンドなのにちょっと寂しいなと思い,今回FRDを活用した記事を書いてみることにしました。
周波数応答データ(FRD)モデル
まず,「周波数応答」は次のような周波数ベクトル(freq)と対応する複素数ベクトル(resp)の組でデータとして表すことができます。
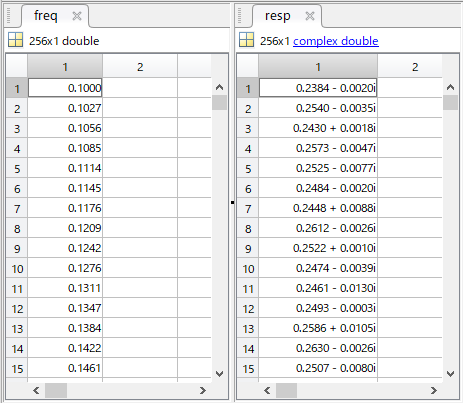
元データはFRDのExampleで使われているものからもらってきました。
openExample('controls_id/CreateFrequencyResponseModelFromDataExample')
load('AnalyzerData.mat')
「複素数の列で表されても何が何だか…」と思われるかもしれません。
周波数応答というのは,「特定の角周波数$\omega$ のsin波をシステムに入力したときに,その信号が何倍くらいに増幅され,どのくらいの遅れを作るか」というものでした。その増幅率がゲイン,その遅れが位相(遅れ)と呼ばれるものです。
上記の各複素数値は,ある周波数に対するゲイン$g$と位相$\theta$ の2つの情報を,一つの複素数 $g e^{j \theta} (=g \cos \theta + jg\sin \theta)$でコンパクトに表してしまったものだと思えば大丈夫です。
システムの応答をFFTなどで周波数解析すると必然的に出てくる形式でもあります。
何はともあれ,上記の周波数ベクトルfreq および周波数応答respを使ってFRDオブジェクトを生成することができます
sys = frd(resp, freq)
sys =
周波数 (rad/s): 応答
------------ --
0.1000 2.384e-01 - 1.951e-03i
0.1027 2.540e-01 - 3.511e-03i
0.1056 2.430e-01 + 1.807e-03i
0.1085 2.573e-01 - 4.672e-03i
% ... 略 ...
92.1947 1.394e-06 + 7.048e-04i
94.7263 -7.793e-05 + 8.046e-04i
97.3274 -1.897e-04 + 6.147e-04i
100.0000 1.116e-05 + 6.157e-04i
連続時間の周波数応答です。
大げさなことは何もなく,基本的には周波数の実数ベクトルと応答の複素数ベクトルを並べただけのものです。
ただし,tfやssと同じ数値線形時不変(LTI)モデルの仲間でもあり,なかなか扱いやすいものになっています。以下で色々いじりながら紹介してみます。
ちなみにMatlabの使用バージョンはMatlab R2023b Update 4,使用ツールボックスはControl System Toolbox です。
描画
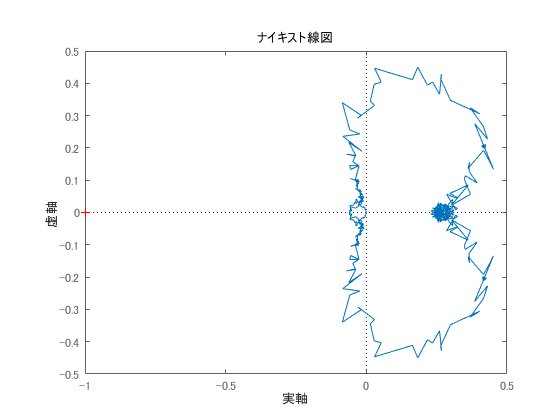
周波数応答の複素数列をそのまんま複素平面にプロットしたものがナイキスト線図ですが,tfやssと同じクラスなのでnyquistで描画できます。
figure
nyquist(sys)
モデルからは出てこない生データらしい良い汚さですね(?)。
各複素数の大きさを取るとゲイン,偏角を取ると位相が算出できますが,ボード線図を描きたいだけであればabsやangleを使わなくともそのままbodeで描画できます。
figure
bode(sys)
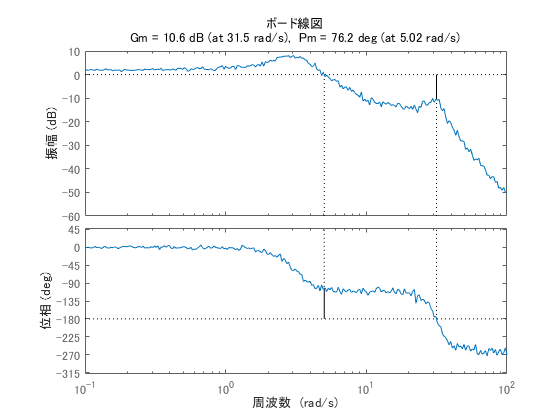
ボード線図が描画できるということは,ゲイン余裕,位相余裕も出せます。
figure
margin(5*sys) % sysのままだと図的につまらないので5倍する
元データのサンプルが細かいのでわかりづらいですが,拡大してみるとちゃんと位相orゲイン交差周波数を出すためにデータ補完してくれています。

ゲイン余裕,位相余裕が出せるということは…
isstable(sys)
次を使用中のエラー: DynamicSystem/isstable
Cannot assess the stability of FRD models.
さすがに無理だったみたいです。
ちなみにzero,poleは出せません。データに極も何もないですからね。
計算
伝達関数モデルや状態空間モデルのように加減乗除できます。
先ほど定数ゲインを乗じることができましたね。
5*sys
ans =
周波数 (rad/s): 応答
------------ --
0.1000 1.192e+00 - 0.0098i
0.1027 1.270e+00 - 0.0176i
0.1056 1.215e+00 + 0.0090i
0.1085 1.287e+00 - 0.0234i
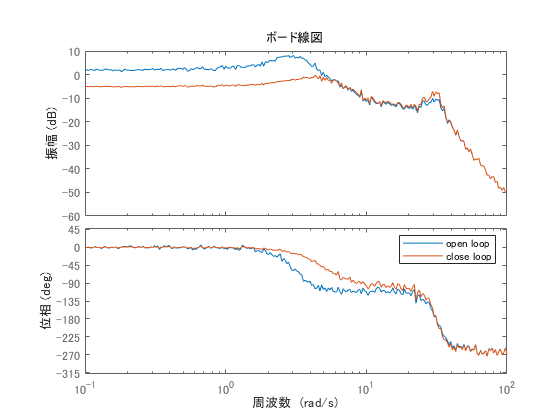
「開ループ特性を閉ループに変換したいな~」
ということで開ループ応答($L$)から閉ループ応答($T=L/(1+L)$)を算出したりできます。
L = 5*sys; % 適当な開ループ応答
T = L/(1+L); % 閉ループ応答
figure
bode(L, T)
legend('open loop', 'close loop')
制御器×制御対象も当然できます。
まずは適当なPID制御器を伝達関数モデルで作ります。
Kp = 5;
Ki = 2.5;
Kd = 0.1;
pid_tf = tf([Kd Kp Ki], [1 0])
pid_tf =
0.1 s^2 + 5 s + 2.5
-------------------
s
連続時間の伝達関数です。
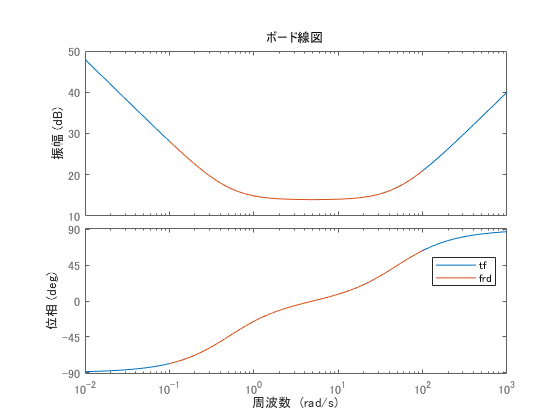
frdコマンドを使って,角周波数freqについてのFRDに変換します。
pid_frd = frd(pid_tf, freq);
figure
bode(pid_tf, pid_frd)
legend('tf', 'frd')
freqの領域に限ってですが,上手く変換できているみたいですね。
次に,sys*pid_frdとかけ合わせます。
figure
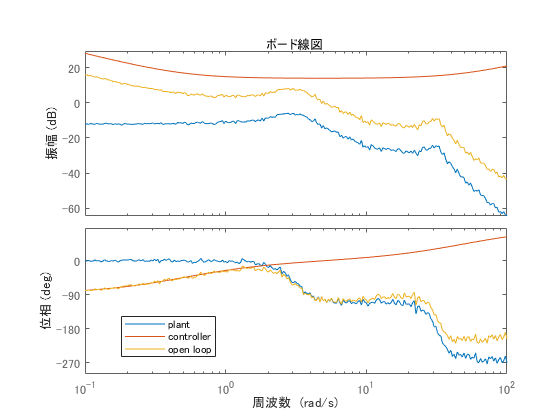
bode(sys, pid_frd, sys*pid_frd)
legend('plant', 'controller', 'open loop')
PID制御器の周波数特性により,全体的にゲインを上げて,低周波ゲインを上げ,高周波位相を進めていることが確認できますね。
実は伝達関数モデルをFRDに変換しないでそのままかけちゃうこともできます。
(かけた後はFRDになる)
figure
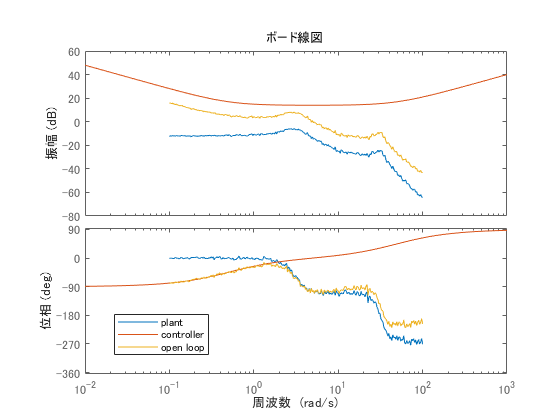
bode(sys, pid_tf, sys*pid_tf)
めっちゃ便利!
一般的に,制御対象の特性はまず実測データとして得られるものだと思います。一方で,制御器の特性はまず伝達関数モデルとして表現されるものだと思います。制御対象の特性を伝達関数でモデル化することなく,制御器を周波数特性データにすることもなく,お互いより少ない加工で,シームレスにかけ合わせられるのが良いですね。
おわりに
sysのボード線図を見て,これが2次遅れ系+2次遅れ系なのか,そうでない何かなのか,正直私にはわかりません。
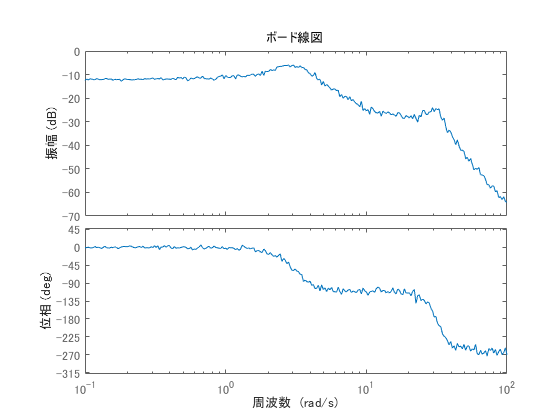
しかし,データをデータのまま処理して新しい特性を導く(予測する) ということが可能であれば,モデル化の工程を一旦飛ばして,このままループ整形してしまうというのも一つの選択肢ではないでしょうか。
最適化アルゴと組み合わせれば,「ゲイン余裕と位相余裕とバンド幅を目的関数に含めたパラメータ最適化2」なんてこともできますね。
今回使った周波数特性データはFRDの公式Exampleのものでしたが,ご自身でFRA装置を使って測定されたデータや,HDDサーボ制御設計のベンチマークモデル Magnetic-head positioning control system in HDDsの特性データや,Simulink Control Designの周波数応答推定器(frestimate)をご自身のモデルに適用して得たFRDを使ってみても面白いかもしれないですのでぜひお試しください。
この記事を書いたきっかけ
ゲイン線図・位相線図のデータを使って,2つのシステムの加減乗除やボード線図描画,安定余裕の算出ができる独自クラスを一生懸命書いちゃったことがあるからです。交点の計算とか,めんどくさかったなぁ…
-
時間応答波形や周波数応答を見てPIDゲインを調整する,というのもモデルフリーなやり方ですが,最近は「データドリブン制御設計」なるものが産業界で流行っているので,こっちを意識してもらうとよいです。 ↩
-
ここまでやってみたかったけど時間切れ… Global Optimization Toolboxまで買ったのに… orz ↩