2024年本屋大賞、宮島未奈さんの成瀬は天下を取りにいくの印象的な書き出し、「島崎1、わたしはこの夏を西武に捧げようと思う」 のオマージュです。
対象読者
- 「成瀬は天下を取りにいく」をまだ読んでいない全国民
- 「成瀬は信じた道をいく」をまだ読んでいない全国民
- (モンテカルロ法やPythonでの実装に興味があるエンジニア)
はじめに
 |
 |
宮島未奈さんのデビュー作にして、今年の本屋大賞を受賞した「成瀬は天下を取りにいく」。本当に良かったです。爽快な読後感で、続編の「成瀬は信じた道をいく」も次の日に本屋に行って買いました。
両作とも滋賀を舞台に、主人公の成瀬あかりを中心に描いた、多視点短編小説です。成瀬は小さい頃からなんでもできるスーパー女子で、とにかく変わっている。それが故に敬遠される描写もあります。だけど本人は一切気にしていない。気にしていない風に装っているわけではなく、本当に気にしていない。自分の興味まっしぐらな姿勢に惹かれます。
全体を通して、短編集でありながら、交わることのなかった人々が成瀬を介して結びついていく展開です。特に二作目、初めはいろんな人から変人扱いをされるんですが、次第に成瀬の人間性に惹かれてハマっていく第三者視点が、読者の目線と被る部分もあってとても良かったです。人を選ばない、万人におすすめできる小説です。
本題
タイトル詐欺になってしまうので、本題。
元の文法に寄せようとしてタイトルが不明瞭なので、まずは問いを仕上げます。
「島崎、私は(滋賀県に対する)琵琶湖(の面積比)を近似的に求めようと思う」
実はこれは県民にとっては踏み絵のような問いです。小学校でのフローティングスクールで近似解を教わるからです。フローティングスクールというのは滋賀の全小学5年生が「うみのこ」という学習船に乗って琵琶湖の上で寝食を共にし、琵琶湖の歴史を学ぶイベントです。
他府県民は残念ですがうみのこには乗れません。代わりにミシガンにどうぞ。ちなみに一作目の作中でも「レッツゴーミシガン」というタイトルの話が登場します。
モンテカルロ法
代数的に琵琶湖の面積比を求めるのは難しいので、今回はモンテカルロ法を使います。
詳細は別の記事を参照してほしいのですが、簡単に言うと「十分に多くの試行回数を設定し、滋賀県上空から一様に落下した場合に、琵琶湖に落ちた回数の割合」は、滋賀県全体に対する琵琶湖の面積比に近似できる、という考え方に基づいています。
ここで、十分に多くの試行回数というのはどのくらいでしょうか?実際には、求める精度によって必要な試行回数は異なります。当然、高い精度で面積比を求めたい場合は、より多くの試行が必要です。
真の比率を $R$ とすると、県外に着地する場合を除外することで、各試行は成功確率 $R$ のベルヌーイ試行に従います。ベルヌーイ試行とは、成功か失敗かの二択の結果を伴う試行です。今回の問題では、試行ごとに「琵琶湖に落ちた」か「陸地に落ちた」かという二択の結果を繰り返し、その成功(琵琶湖に落ちた)の割合を計算します。
試行回数が十分に増えると、大数の法則により観測された割合(推定された比率)は真の比率 $R$ に近づいていきます。また、中心極限定理により、この観測された割合の分布は正規分布に近づくため、母比率 $R$ に対して信頼区間を使った区間推定を行うことができます。
標準化などを行うことで容易に以下の不等式まで導出できます。(詳細)
\hat{R} - z_{\frac{\alpha}{2}} \times \sqrt{\frac{R(1-R)}{n}} \leq R \leq \hat{R} + z_{\frac{\alpha}{2}} \times \sqrt{\frac{R(1-R)}{n}}
ここで$\hat{R}$は一致推定量なので左右の$R$を置き換えてあげて、実装フェーズでは $z_{\frac{\alpha}{2}}$について、95%信頼区間( $\alpha=0.05, z_{\frac{\alpha}{2}}=1.96$ )で計算することにします。
実装
実際に滋賀の上空から一様に落下することは難しいので、滋賀の画像を用いつつ乱数を発生させることで擬似的に落下しようと思います。画像は illust image を利用しました。( 画像リンク )
カラーマップを眺めたところ若干の濃淡があったので、琵琶湖, 陸地(県内), 県外, 右下の著作権表示の代表値を取って、4つのうちの近い値に分類する前処理をしています。
コードを展開 (Python)
from pathlib import Path
import random
import operator
import matplotlib.pyplot as plt
import numpy as np
import cv2
random.seed(42)
np.random.seed(42)
class ColorConverter:
def __init__(self, target_colors: list[tuple]):
""" 指定されたターゲット色に画像を変換するクラス """
self.target_colors = target_colors
def convert(self, image):
""" ターゲット色に変換 """
height, width, _ = image.shape
for h in range(height):
for w in range(width):
image[h, w] = self.closest_color(image[h, w])
return image
def calc_distance(self, color1: tuple, color2: tuple) -> float:
return np.linalg.norm(np.array(color1) - np.array(color2))
def closest_color(self, color: tuple) -> tuple:
""" ターゲット色からcolorに最も近い色を返す """
min_distance = 1000
closest_color = self.target_colors[0]
for target_color in self.target_colors:
distance = self.calc_distance(color, target_color)
if distance < min_distance:
min_distance = distance
closest_color = target_color
return closest_color
class Shiga:
GREEN = np.array([0, 153, 0]) # 陸地
WATER = np.array([126, 218, 255]) # 琵琶湖
WHITE = np.array([255, 255, 255]) # 県外
GRAY = np.array([178, 178, 178]) # 著作権表示
SHIGA = [GREEN, WATER]
BIWAKO = [WATER]
def __init__(self, image_path: Path = "./shiga.png"):
# 画像を読み込む処理
self.image = cv2.imread(image_path)
self.image = cv2.cvtColor(self.image, cv2.COLOR_BGR2RGB)
# ターゲット色への変換 (濃淡を除去)
target_colors = [self.GREEN, self.WATER, self.WHITE, self.GRAY]
self.image = ColorConverter(target_colors).convert(self.image)
self.height, self.width, self.channels = self.image.shape
def estimate_biwako_area(self, attempt: int = 100000) -> dict[int, int]:
""" モンテカルロ法で琵琶湖の面積比を求める """
biwako_count = 0 # 琵琶湖の中に入った回数
shiga_count = 0 # 滋賀県内に入った回数
records = dict() # key回の試行の内(県外は除く)、value回琵琶湖に落下
while shiga_count <= attempt:
h = random.randint(0, self.height - 1)
w = random.randint(0, self.width - 1)
if self.inside_shiga(h, w):
shiga_count += 1
if self.inside_biwako(h, w):
biwako_count += 1
if shiga_count and (shiga_count % 100 == 0):
records[shiga_count] = biwako_count
return records
def inside_shiga(self, h: int, w: int) -> bool:
""" 県内ならTrueを返す """
return any(np.array_equal(self.image[h, w], color) for color in self.SHIGA)
def inside_biwako(self, h: int, w: int) -> bool:
""" 琵琶湖に沈んだならTrueを返す """
return np.array_equal(self.image[h, w], self.WATER)
if __name__ == "__main__":
shiga = Shiga("./shiga.png")
records = shiga.estimate_biwako_area()
結果
信頼区間を表示するコード
records = shiga.estimate_biwako_area()
### 1. 信頼区間(95%)の描画 ###
print("Attempt | Biwako | R_hat | lower bound | upper bound")
for attempt in [100, 1000, 10000, 100000]:
biwako_count = records[attempt] # 琵琶湖の沈んだ入った回数
biwako_ratio = biwako_count / attempt # 琵琶湖に沈んだ割合
margin_of_error = 1.96 * np.sqrt(biwako_ratio * (1 - biwako_ratio) / attempt)
lower_bound = biwako_ratio - margin_of_error
upper_bound = biwako_ratio + margin_of_error
print(f"{attempt:7} | {biwako_count:6} | {biwako_ratio:.4f} | {lower_bound:11.4f} | {upper_bound:11.4f}")
Attempt | Biwako | R_hat | lower bound | upper bound
100 | 14 | 0.1400 | 0.0720 | 0.2080
1000 | 174 | 0.1740 | 0.1505 | 0.1975
10000 | 1716 | 0.1716 | 0.1642 | 0.1790
100000 | 16832 | 0.1683 | 0.1660 | 0.1706
試行を重ねるにつれて信頼区間が狭くなっているのが分かります。
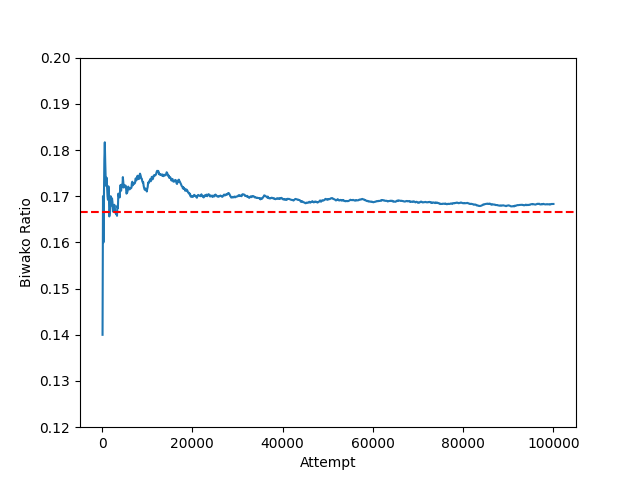
琵琶湖の比率を描画するコード
records = shiga.estimate_biwako_area()
### 2. 比率の遷移のグラフを描画 ###
fig, ax = plt.subplots()
x = list(records.keys())
y = [records[attempt] / attempt for attempt in x]
ax.plot(x, y)
ax.set_xlabel("Attempt")
ax.set_ylabel("Biwako Ratio")
ax.set_ylim(0.12, 0.2)
# 6分の1に線を引く
ax.axhline(y=1/6, color="red", linestyle="--")
plt.show()
6分の1に赤線を引いていますが、(画像が正しければ)実際はもうちょっと大きいのかも。
おわりに
コードを書いている時に気づいたんですが、すでに近似済みのデジタル画像を用いているので、前処理後のカラーマップの比率を取れば終わりなんですよね。
というのはさておき、成瀬シリーズ3作目が執筆中とのことなので楽しみです。以上です。
-
成瀬あかりと同じマンションに住む親友の島崎みゆきです。 ↩