世界一難しいナンプレを1秒で解く方法

はじめに

いきなりですが、下の数独解けますか?

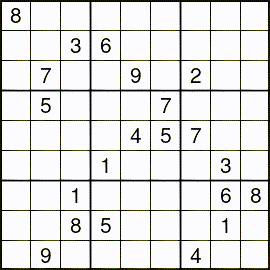
↑フィンランドの数学者Alto Inkala氏が作成した世界一難しいと言われる数独です。
これをpythonの力を借りてプログラミングで解いてみようという記事です。

そもそも数独って?

・空欄のマスに1~9の数字を入れて埋めます。
・ただしそのマスが属する列、行、ブロックに重複した数字が入ってはいけません。
・ブロックとは太線に囲まれた3×3の正方形のことです。
・全て埋められたら無事終わりです。

アルゴリズム

今回は深さ優先探索によるバックトラック法で解いてみます。
ざっくり挙動を説明すると、

1. 空欄を順に見ていき数字を1から順番にとりあえず入れてみる
2. 1で矛盾が発生しなかったら次の空欄マスまで進む
3. 矛盾が発生した&数字を9まで見た場合ひとつ前の空欄まで戻る
4. 全て埋まったら(最後のマスに矛盾が生じなかったら)終了

3で逆戻りすることからバックトラックと呼ばれます。
これは再帰関数で楽に実装できそうですね。やってみましょう。

実装

データの受け取り

9×9のグリッドのデータを受け取りたいです。2次元配列を使うといいです。
(空欄は0としてデータを保存し1~9以外の文字を空欄と認識します)

grid = [[int(x) if x.isdigit() else 0 for x in input()] for _ in range(9)]

入力例↓ (「*」, 「.」, 「0」などは空欄として認識。 (以降「.」を使う))

8.....**0
..36.....
.7..9.2..
.5...7...
...457...
...1...3.
..1....68
..85...1.
.9....4..

lambda関数はちょっとした関数を定義したいときに便利ですね。次に行きます。
（21/11/15 01:49追記）
@shiracamus さんのご指摘のように、入力形式を変更しました。
(コードがスッキリしました、、)

矛盾があるかどうか調べる (possible関数)

先にコードを見せます。

# grid[y][x]にkを入れることは可能か
def possible(grid, x, y, k):
    # 行のチェック
    if k in grid[y]:
        return False
    # 列のチェック
    if k in [line[x] for line in grid]:
        return False
    # ブロックのチェック
    sx, sy = x // 3 * 3, y // 3 * 3  # (x, y)が属するblockの左上の座標を(sx, sy)
    return all(grid[sy+dy][sx+dx] != k for dx in range(3) for dy in range(3))

順に説明します。引数のgridについては先ほど受け取った9×9の二次元配列です。

各マスの座標をヨコ方向をx,縦方向をyとして定義します。左上のマスは(x, y) = (0, 0)となります。右下はどうでしょうか??(8, 8)ですね。(0-indexedであることに注意）

kは今まさにマス(x, y)に入れようと試みている数字です。grid[y][x]は(x, y)です。

矛盾のチェックにはマス(x, y)が属する行、列、ブロックのデータが必要です。行については簡単ですね。grid[y] (上から(y+1)番目のグリッドの要素=>(x, y)が属する行)で取れます。ここに既にkという値が含まれるならgrid[y][x]にkを入れることは不可能ですからFalseを返します。

# 列のチェック
if k in [line[x] for line in grid]:
    return False

続いて列のチェックです。先程よりめんどうですね。リスト内包表記を使います。(gridの要素をforで回すと各行(line)を取得でき,そこから該当する値のみを抽出するイメージです)

最後にブロックのチェックです。更にめんどうですね。まず以下の問題を考えます。
あるマス(x, y)に対してそのマスが属するブロックの最左上のマスの座標はなにか?
((sx, sy)を(x, y)に対する最左上マスの座標とします。これは一意に求まります)

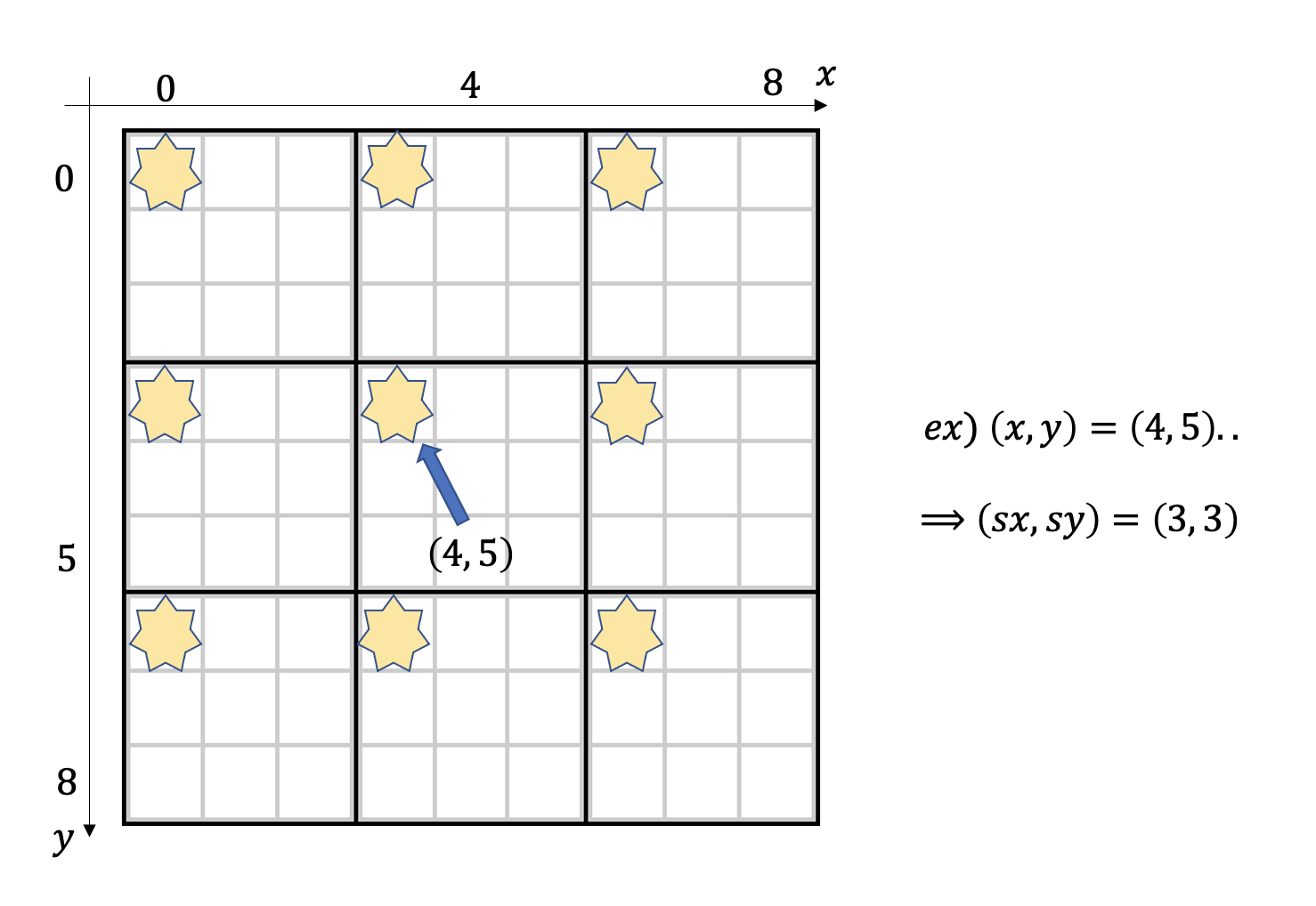
左上のマスは黄色の星で塗られたマスが全てです。各座標は順に(0, 0),.., (0, 6), (3, 0),...(6, 6)です。何やらいい性質がありそうですね...そう、すべて3の倍数です。(ここから少し数学)

(x, y)の属するブロックの左上マスの座標(sx, sy)はx, yを超えない最大の3の倍数として表現されます。x, yそれぞれについて3で割った商に3をかけた値として求めることができます。

ここまでできればあとは簡単。dx, dyを0から2まで動かした場合のgrid[sy+dy][sx+dx]がそのブロックの値です。あとは同じように重複判定するだけです。

（21/11/15 16:05追記）
最終のblock判定のところを以下のように訂正しました。
(訂正前のものでも正常には動きますが冗長であったため..)

訂正前↓

block = [grid[sy+dy][sx+dx] for dx in range(3) for dy in range(3)]
if k in block:
    return False
return True

訂正後↓

return all(grid[sy+dy][sx+dx] != k for dx in range(3) for dy in range(3))

スマートになりました。@shiracamus さんありがとうございます。

順にマスを見る / 終了判定 (solve関数)

あと少しで終わりです。まず順を定義します。順とは左上からヨコ方向にマスを見ていきマスの終端を超えたらひとつ下のマスまで降りてx座標をもう一度０からスタートさせます。漢字の「三」の書き順のイメージでマスを見ていきます。

上記のように定義することで終了判定はy座標が終端を超えたかどうかで判定できます。

# 今(x, y)マスを見ている。
def solve(grid, x, y):
    if y == 9:  # 終了判定
        return True
    if x >= 9:  # 1行下がる
        return solve(grid, 0, y+1)
    if grid[y][x] != 0:  # 既にマスが埋まっている
        return solve(grid, x+1, y)
    for k in range(1, 10):
        # 先ほど定義した関数で値kをgrid[y][x]に入れられるか判定
        if possible(grid, x, y, k):
            grid[y][x] = k
            if solve(grid, x+1, y): # 次のマスを見る
                return True
            grid[y][x] = 0  # ここが重要
    return False

下から2行目にgrid[y][x]=0としている行がありますね。ここがバックトラックの本質部分になります。再帰関数の挙動を理解していないと少し難しいです。

また正常に終了した場合のみTrueを返すようにしています。

お疲れ様でした。これで数独ソルバーは完成です。

まとめ

実装の部分では以下を定義しました。
・データの入力部分
・矛盾がないかのチェック
・順に見ていく部分 / 終了判定

上記の部分だけでも解を求めることは可能ですが、いくつか機能を付け加えました。
・ データの入力段階での矛盾チェック (possible関数を用います)
・ 計算時間の測定 (タイトル詐欺になってしまうので...)

各関数に型のアノテーションも足しました。全文は以下になります。

import time
from typing import List


def possible(grid: List[List[int]], x: int, y: int , k: int) -> bool:
    if k in grid[y]:
        return False
    if k in [line[x] for line in grid]:
        return False
    sx, sy = x // 3 * 3, y // 3 * 3
    return all(grid[sy+dy][sx+dx] != k for dx in range(3) for dy in range(3))


def solve(grid: List[List[int]], x: int, y: int) -> bool:
    if y == 9:
        return True
    if x >= 9:
        return solve(grid, 0, y+1)
    if grid[y][x] != 0:
        return solve(grid, x+1, y)
    for k in range(1, 10):
        if possible(grid, x, y, k):
            grid[y][x] = k
            if solve(grid, x+1, y):
                return True
            grid[y][x] = 0
    return False


def main():
    # データの受け取り
    grid = [[int(x) if x.isdigit() else 0 for x in input()] for _ in range(9)]

    # 事前に矛盾がないかチェック
    for x in range(9):
        for y in range(9):
            if not grid[y][x]:
                continue
            k = grid[y][x]
            grid[y][x] = 0
            if not possible(grid, x, y, k):
                print("Impossible")
                return
            grid[y][x] = k

    # 計算時間の測定
    start = time.time()
    can = solve(grid, 0, 0)  # 計算開始
    end = time.time()

    print("\nanswer:")
    if not can:
        print("Impossible")
        return

    for line in grid:
        print(*line, sep="")
    print(f"time: {end - start:.3f}s")


if __name__ == '__main__':
    main()

コピペでファイルを保存して実際にterminalで実行してみましょう。
（ここではNumpre.pyとします)

\dir $ python3 Numpre.py
8........
..36.....
.7..9.2..
.5...7...
....457..
...1...3.
..1....68
..85...1.
.9....4..

answer:
812753649
943682175
675491283
154237896
369845721
287169534
521974368
438526917
796318452
time: 0.374s

はい、世界一難しいナンプレの解を0.374秒で求めることができました。
他の例でももちろん正常に動きます。

細かい話

計算量についてですが、マスが埋まっていくにつれて入れられる数値というのはどんどん限られていくので想像よりは再帰が深くなりません。実際に上の例において、globalにcnt変数を定義して再帰の回数を数えてみると74025回しか呼ばれないことが確かめられます。

終わりに

バグを見つけたら報告よろしくお願いします。