#この記事を書いた理由
AI人材目指してPythonを勉強しているのですが、集合型の内容がもろ数Aの集合の内容だったので今後使うことが多いのかなと思ったので、まとめます。
Pythonの勉強はこちらを活用して進めてます。
Python入門者のための学習ロードマップ【ブログでも独学可能】
現役シリコンバレーエンジニアが教えるPython 3 入門 + 応用 +アメリカのシリコンバレー流コードスタイル
Python, set型で集合演算（和集合、積集合や部分集合の判定など）
#集合型（セット）とは
- 中にある要素が重複せず、順番がなく番号が定義されていない要素の塊
- シーケンス型（文字列、タプル、リスト）の親戚みたいな感じ
- { }の中にコンマで区切って定義
- set( )関数でデータタイプを集合型（setタイプ）に変えて定義
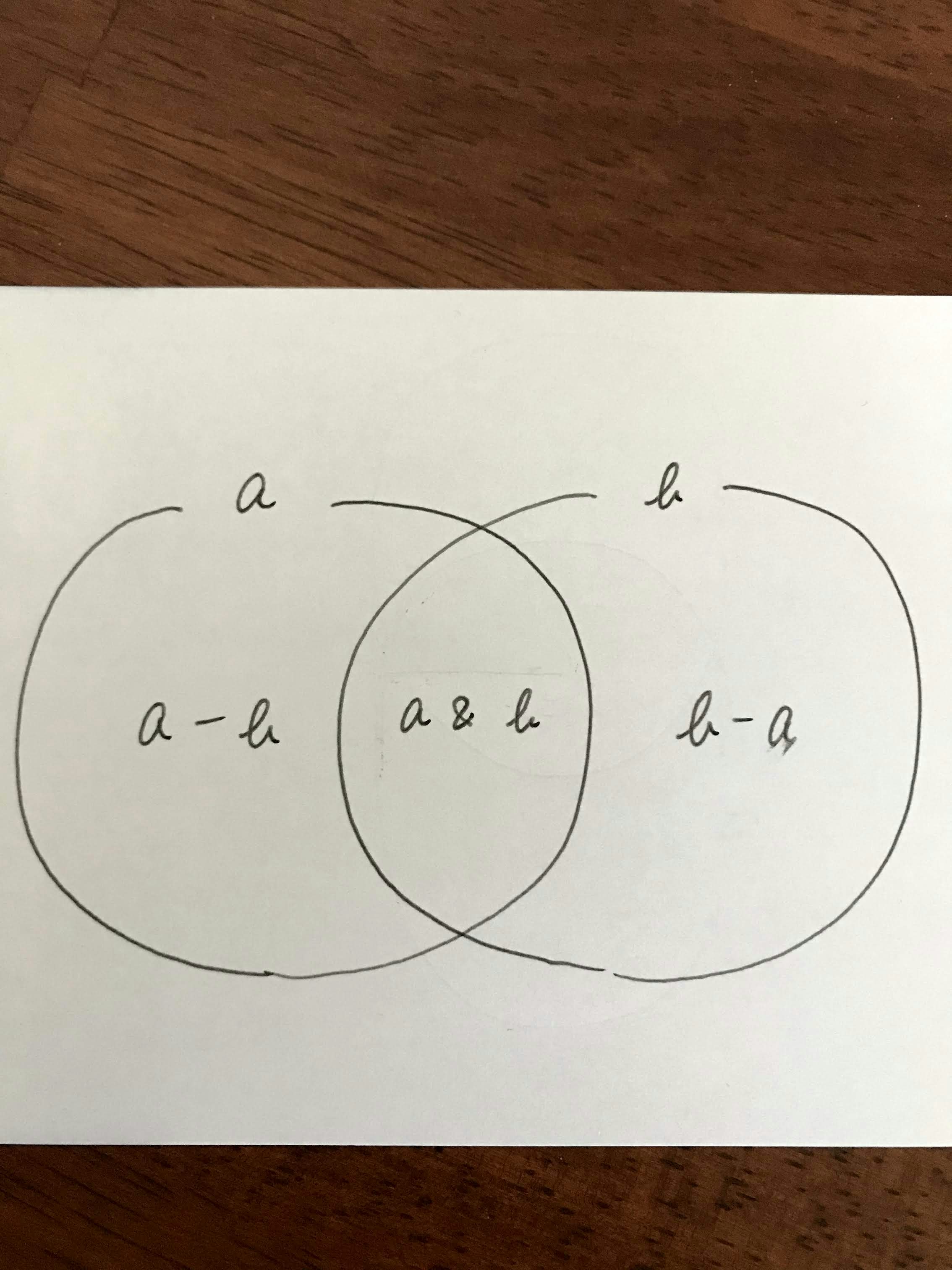
#図示してみた
２つの集合型aとbがあったとする。
- aとbで共通している集合（積集合）：
a & b - aから「aとbで共通している要素（積集合）」を除いた集合（差集合）：
a - b - bから「aとbで共通している要素（積集合）」を除いた集合（差集合）：
b - a
は以下の図のイメージ。
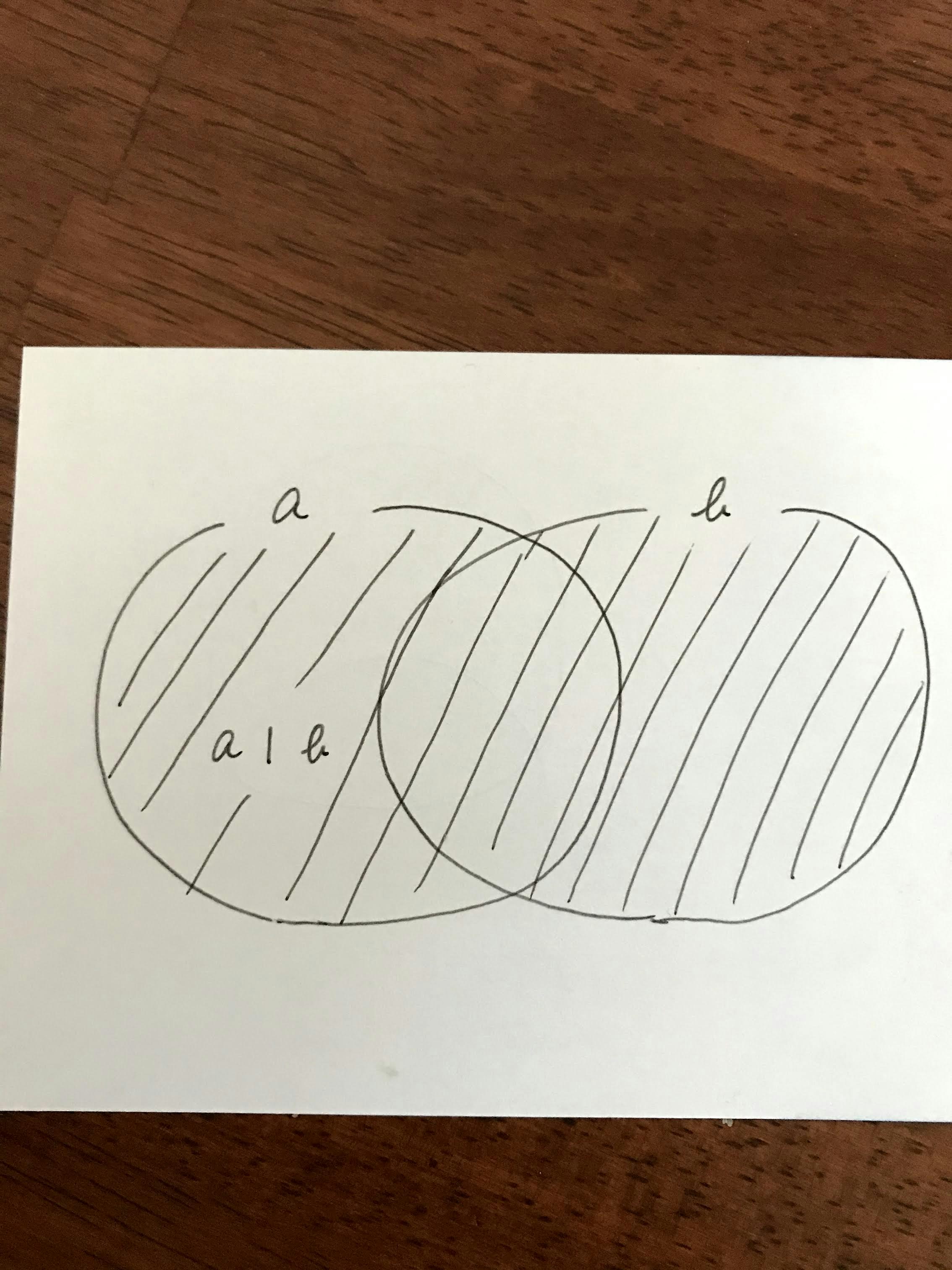
- aとbの要素を全て合わせた集合（和集合）：
a | b
は以下の図のイメージ
-「aに属してbに属さないもの」と「bに属してaに属さないもの」を合わせた集合（対象差集合）:a ^ b
は以下の図のイメージ
#集合体の演算方法
先ほど図示したものを実際にコードで表現してみる。
set.py
# 集合型aとbを定義
a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {2, 4, 6, 8, 10, 12}
# 積集合
print(a & b) #実行結果：{2, 4, 6, 8, 10}
# 差集合
print(a - b) #実行結果：{1, 3, 5, 7, 9}
print(b - a) #実行結果：{12}
# 和集合
print(a | b) #実行結果：{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12}
# 対象差集合
print(a ^ b) #実行結果：{1, 3, 5, 7, 9, 12}
ちなみに集合型の演算にはメソッドも使える。
set.py
# 集合型aとbを定義
a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b = {2, 4, 6, 8, 10, 12}
# 積集合
print(a & b) #実行結果：{2, 4, 6, 8, 10}
print(a.intersection(b)) #実行結果：{2, 4, 6, 8, 10}
# 差集合
print(a - b) #実行結果：{1, 3, 5, 7, 9}
print(a.difference(b)) #実行結果：{1, 3, 5, 7, 9}
print(b - a) #実行結果：{12}
print(b.difference(a)) #実行結果：{12}
# 和集合
print(a | b) #実行結果：{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12}
print(a.union(b)) #実行結果：{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12}
# 対象差集合
print(a ^ b) #実行結果：{1, 3, 5, 7, 9, 12}
print(a.symmetric_difference(b)) #実行結果：{1, 3, 5, 7, 9, 12}
#おわりに
部分集合に関してはまた別の記事にでもまとめてみようかなと。
やはり何かしらアウトプットした方が頭の中が整理できるのでオススメ。
Python、楽しい！