この記事はNSSOL Advent Calendar 2020の7日目の記事です。
本記事の目的
今年の4月頃に提案された論文「Feature Quantization Improves GAN Training」を、1つ1つの処理を図示しながら実装することを目指す記事です。
普段機械学習に関する論文を読んでいると、再現実装のイメージが湧きにくい内容に出くわすことがあります。こうした状況に出くわしたとき、私はよく1つ1つのTensor処理を図として書き出していきながら理解を進めていっており、本論文でそのときのイメージを共有したいと思います。
独自の実験は間に合わなかったため、後日追加します。
モデルだけですが、以下に配置しています。絶賛改良中。
理解不足の部分もあるため、間違いなどあったらコメントをいただけると嬉しいです!
論文概要
実装に移る前に簡単に論文の内容を紹介します。
本論文で解決したいこと
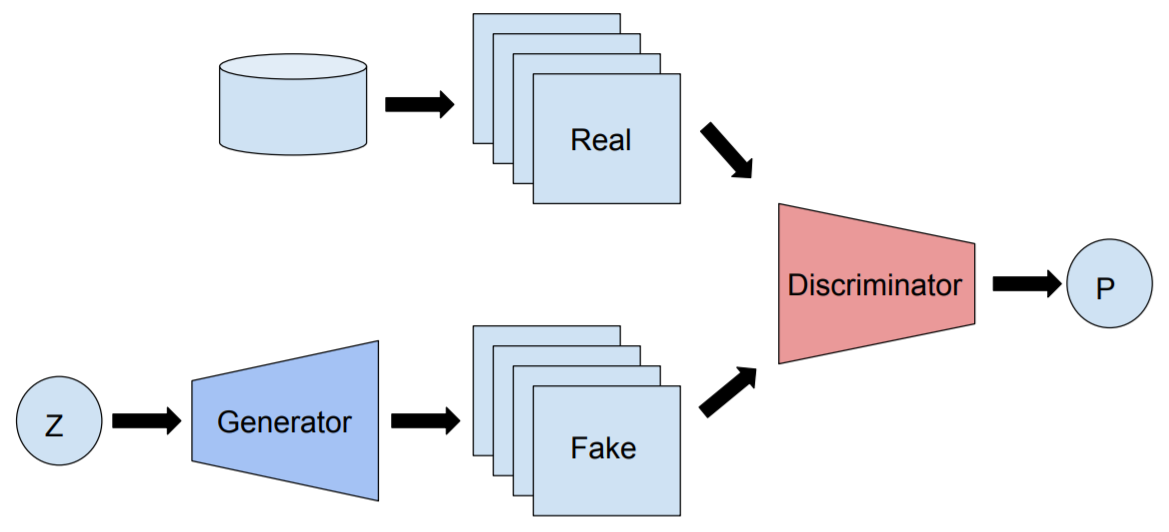
GANの学習を振り返ると、Generatorは訓練データの分布を学習させることで本物に近い画像を生成し、Discriminatorは本物の画像と偽物の画像から本物画像を識別できるようになることを目指します。
理想的な状況では、Generatorが実画像の分布と同じ分布を学習するすることで、実画像と全く同じ偽物画像を生成できるようになります。
しかし、論文中で提示されているように従来のGANでは以下の3つの課題を有しています。
- 勾配降下法で使用するミニバッチが小さい場合、巨大なデータセットの実分布をミニバッチのみで表現することができず、実画像に合うような偽物画像を生成できるパラメータを見つけることが難しい
- ミニバッチを大きくすれば実画像の分布を近似できるが、計算コストが増大してしまう
- 学習中ではGeneratorが学習している偽物画像の分布が変動してしまい、Discriminatorが解くべき分類タスクも変動してしまう
本論文ではこの問題を Vector Quantize(ベクトル量子化) という手法で解決しようとしています。
Vector Quantize(ベクトル量子化)とは
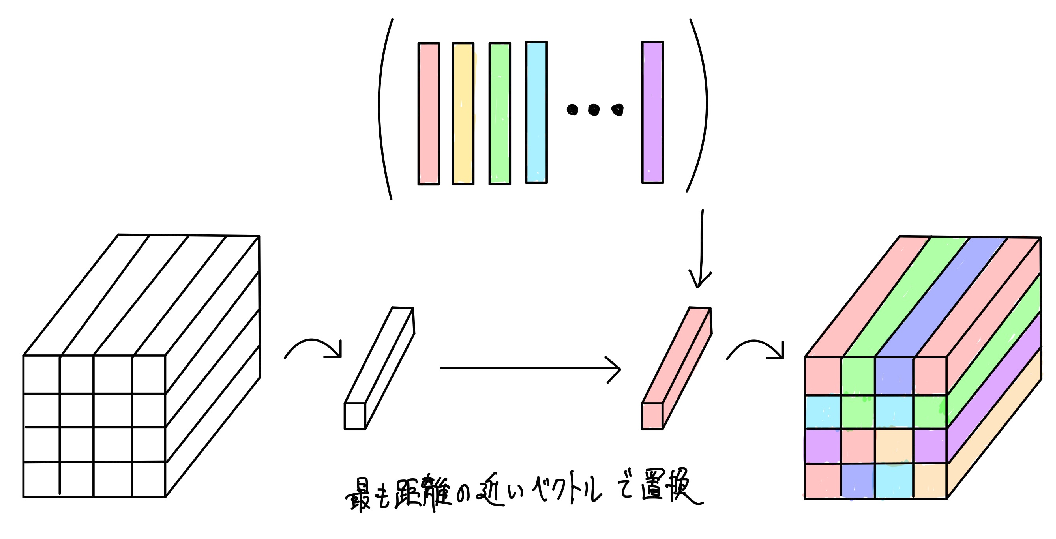
ベクトル量子化は、以下の図のようにBottom Networkから抽出された特徴マップ内の1つ1つの空間的位置に対応する特徴ベクトルを、codebook(Dictionary)内で定義されている有限個のベクトルで置換する手法です。
| 全体像 | 特徴マップの置換 |
|---|---|
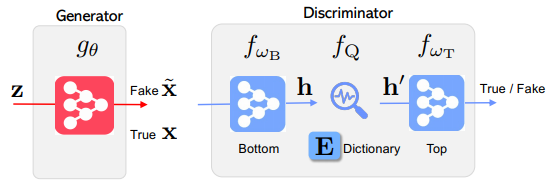 |
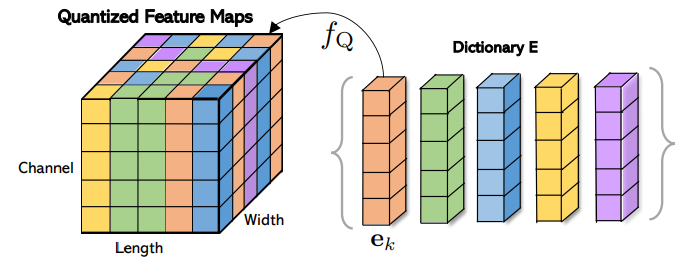 |
特徴マップの表現を、この有限個のベクトルに制限することで、画像の変動に頑強なモデルを構築することを目的としています。
実際に以下の画像で示すように、Discriminatorは画像中の似た領域を同じベクトルで識別していることがわかります。(論文中では、以下の色付けにt-SNEを使用しています。)
このVector Quantize(ベクトル量子化)をGANに適用することで,当時のSOTAに匹敵するFIDを達成しました。画像生成で使用されているBigGANや画像変換で使用されているUGATITなど,様々なモデルに簡単に組み込むことのできる手法です。
この手法はもともとVQVAEで提案されましたが,特徴量を有限のベクトルで置き換える手法自体は様々な論文で出現するテクニックになります.
- Neural Discrete Representation Learning
- Momentum Contrast for Unsupervised Visual Representation Learning
- Latent Video Transformer
ではなぜこの手法が効果を発揮したのかイメージを膨らませていきます。
計算イメージ
畳み込み演算の振り返り
この手法は畳み込み演算を行うことで出力される特徴マップに対して適用するため、まずは畳み込み演算と特徴マップ自体のイメージを掴んでいきます。
ではまず畳み込み演算の計算過程を見てみましょう。
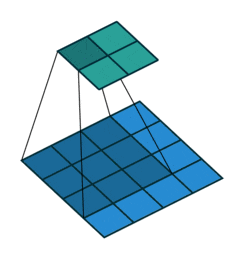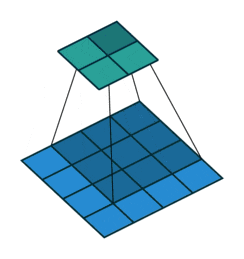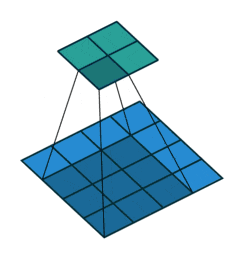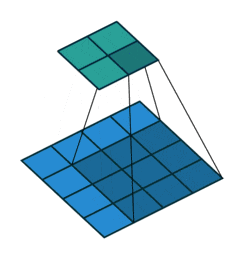
以下の図は4x4の画像に対して、3x3のフィルタを適用している様子を表しています。
https://github.com/vdumoulin/conv_arithmetic/blob/master/gif/no_padding_no_strides.gif
ではこの畳み込み演算を計算することで得られる結果は、どのように解釈することができるのかを考えます。
上の図では、結局のところフィルタを適用する少領域とフィルタ自体の内積を計算しています。ベクトルの内積が、ベクトル同士がどの程度類似しているのかを表現できるように、画像内の少領域とフィルタがどの程度似ているのかを抽出していると考えることができます。
実際に数字の「4」に対して、左下から右上にかかる斜線を検出するフィルタと、水平線を検出するフィルタを適用してみます。
https://docs.google.com/spreadsheets/d/1wIeyDjwIFzwoaueIYTpaac63LvOHUZKnJvQUas9LAmQ/edit?usp=sharing
この結果からわかるように、出力される特徴マップのあるチャンネルに限ってみると、1つ1つの空間的位置に対応する値は、もとの画像に適用されたフィルタとどの程度似ているのかを表しています。
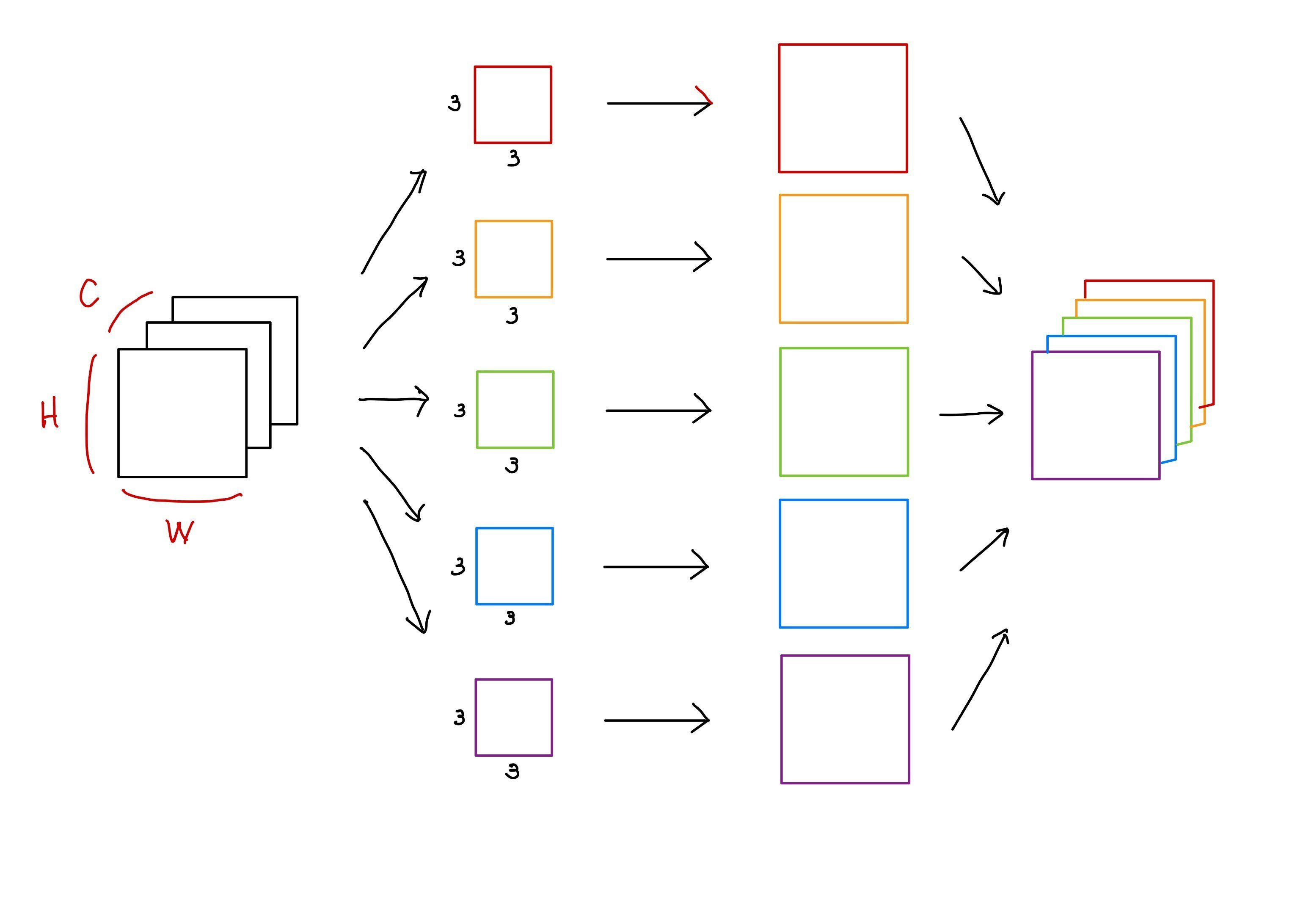
畳み込み演算を計算する際に、3つのチャンネルを有する画像に対して5つのフィルタを適用することを考えてみます。
出力される5つのチャンネルを有する特徴マップのあるピクセルに着目してみましょう。この特徴ベクトル($\in R^{1x1x5}$)を構成する5つの値は、それぞれ異なる特徴量を抽出できるフィルタに対して、どの程度の類似性を有しているのかを示す組み合わせであることがわかります。
例えば、特徴ベクトル($\in R^{1\times 1\times 5}$)を以下のように考えることができます。
| 1-channel | 2-channel | 3-channel | 4-channel | 5-channel | |
|---|---|---|---|---|---|
| フィルタ | 水平線 | 垂直線 | 垂直に近い斜線 | 水平に近い斜線 | 対角線 |
| 類似性 | 2.0 | -1.0 | 3.0 | 1.5 | 0.5 |
畳み込み演算の層をさらに積み重ねていくと、上記のような基本的な特徴量を組み合わせることで、より複雑な特徴量を抽出することができるようになります。
AlexNetの学習済みのモデルの可視化をしてみましょう。
各層で出力される特徴マップに対して、強く活性化しているものを9つまで選択し、入力した画像領域と合わせてみてみると、層が深くなるごとにより複雑な特徴量を学習していることがわかる。
畳み込み演算では、より低次元の特徴量を組み合わせて複雑な特徴量を表現することができています。
ベクトル量子化とは、この低次元の特徴量の組み合わせを有限個に制限することで、画像の少領域の変動に頑強なモデルを学習させることを目的としています。
ベクトル量子化のイメージ
ではベクトル量子化のイメージと対応する実装を考えていきましょう。
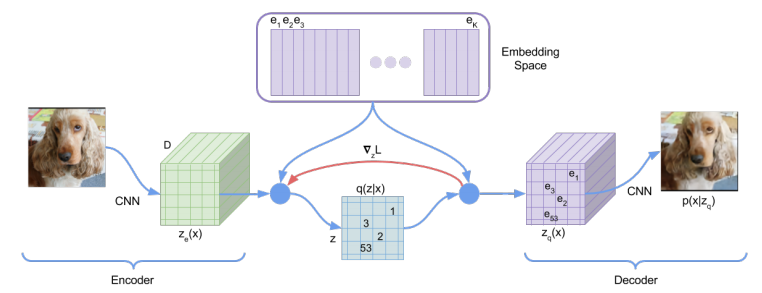
まずベクトル量子化の全体像を示しておきます。以下の図のように、$D$次元のベクトルを$K$個有しているcodebookを使用して、入力される特徴量を、対応するベクトルで置換していきます。
ではベクトル量子化の計算を進めていきましょう。
ベクトル量子化では、入力された特徴マップの1つ1つの空間的位置に対応する特徴ベクトルと、codebook内で定義されている$K$個の特徴ベクトルとの距離を計算し、最も距離の近いベクトルで特徴マップを置換します。
これは数式的には、以下のように計算して出力されたインデックスをもとに置換していきます。
\boldsymbol{h}^{\prime}=f_{\mathrm{Q}}(\boldsymbol{h})=e_{k}, \text { where } k=\operatorname{argmin}_{j}\left\|\boldsymbol{h}-\boldsymbol{e}_{j}\right\|_{2}
上記の計算を実行する前の準備をしていきます。
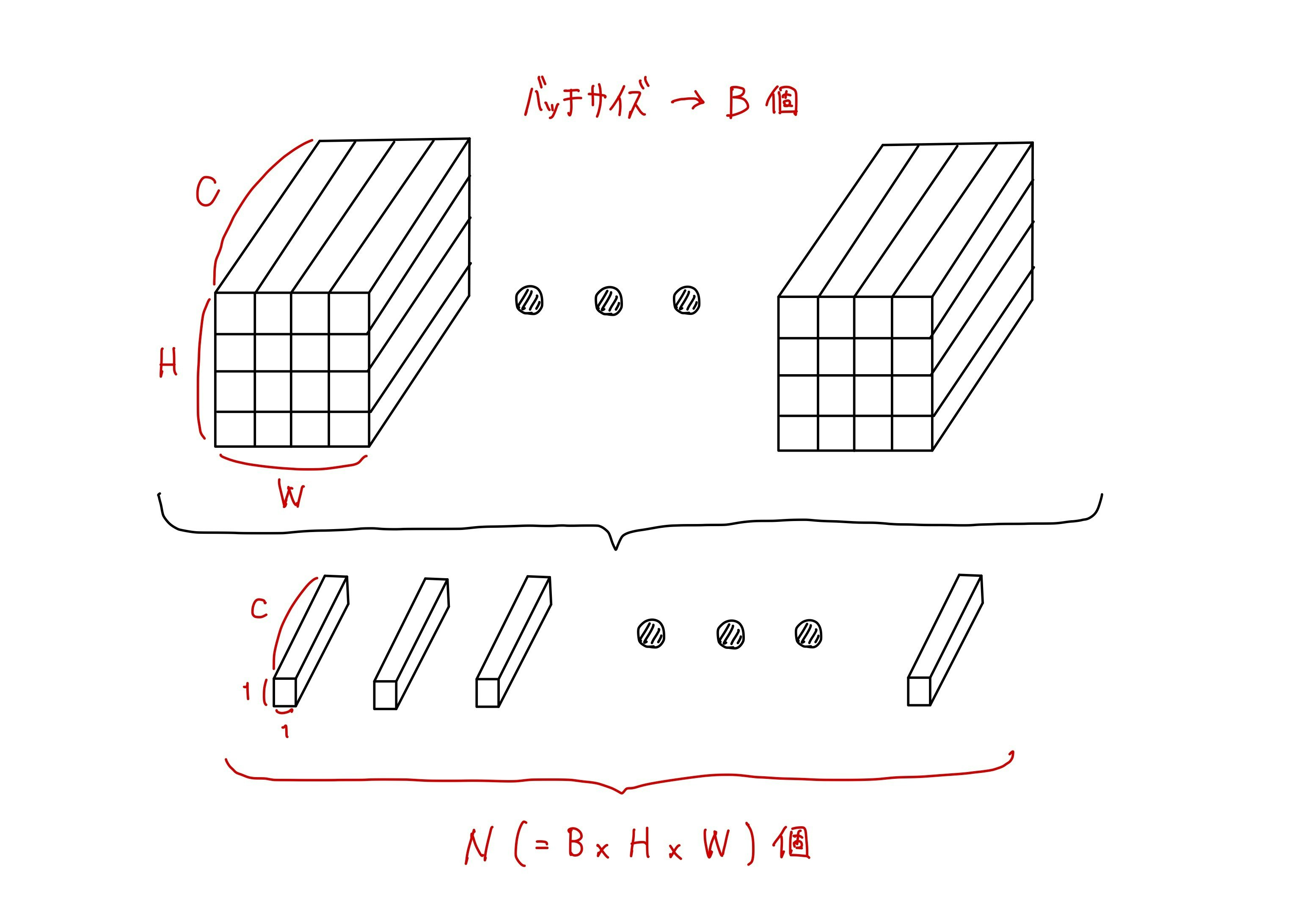
Tensorでの計算上、入力された特徴マップをそのまま使用するよりも、1つ1つのピクセルに対応する特徴ベクトルに並び替えるほうが便利です。
この部分をイメージすると特徴マップ($\in R^{B\times C\times H\times W}$)を以下のように分解することになります。
実装は以下のようになります。
def forward(self, inputs):
# get the shape of the input feature map for reshaping when output
# inputs_shape: [B, C, H, W]
inputs_shape = inputs.size()
# Converts a feature map to the shape of the number of feature vectors and the dimensionality of the feature vectors, to represent them as a set of one by one.
# inputs: [B, C, H, W] --> [B, H, W, C=D(=emb_dim)]
inputs = inputs.permute(0, 2, 3, 1).contiguous()
# flatten: [B, H, W, D] --> [BxHxW=N, D]
flatten = inputs.view(-1, self.emb_dim)
PyTorchの処理に関する補足をしておくと,PyTorchにて
permute()を実行すると,Tensorのメモリが要素順で並んでいる状態ではなくなります.しかしview()でのTensor形状の変換処理は,Tensorが要素順に並んでいる必要があるため,contiguous()を呼び出して並び替えを実行しています.
では特徴ベクトルとcodebook内のベクトルとの距離を計算していきます。
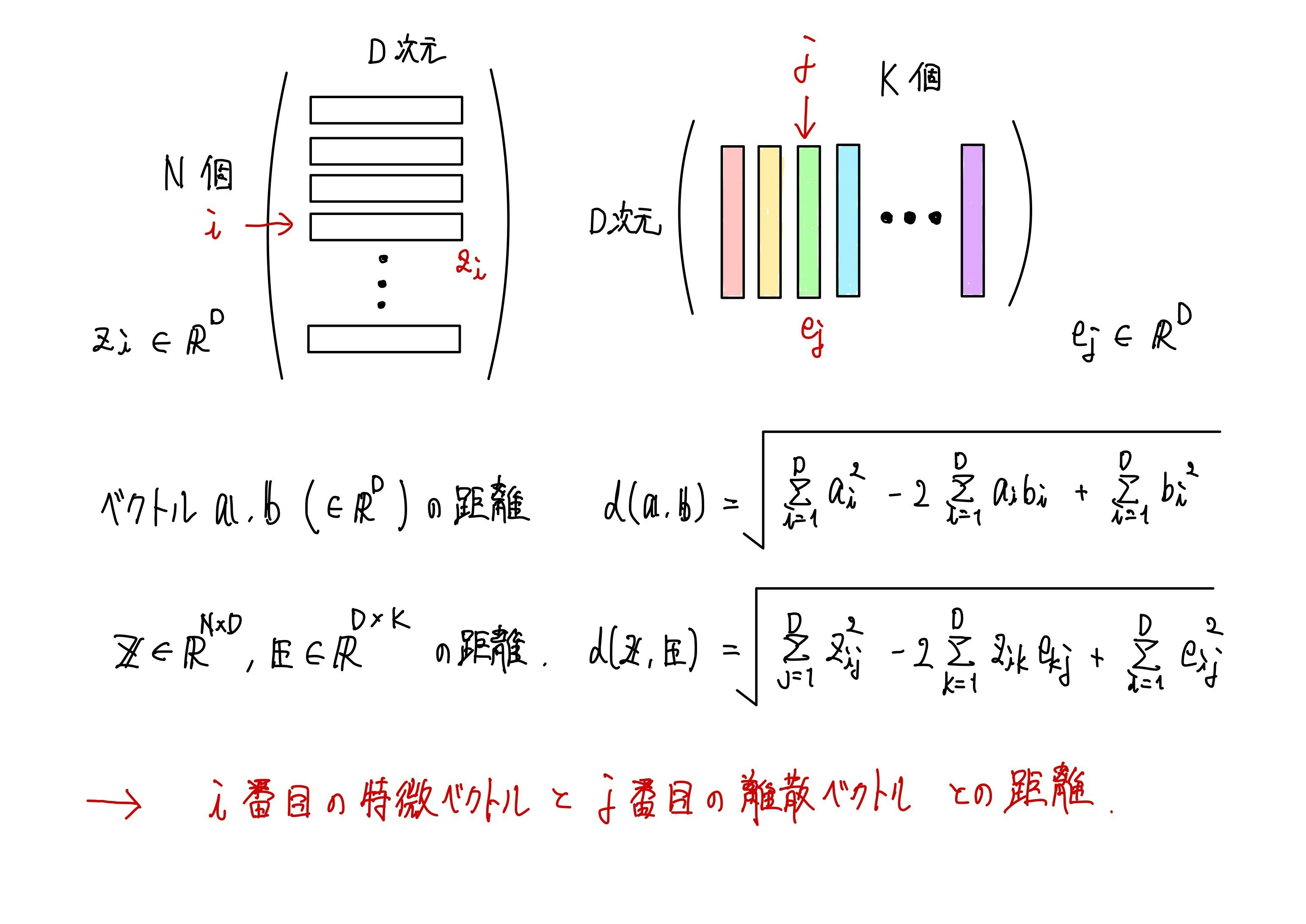
まず2つのベクトル間のユークリッド距離を計算する式は以下のよう表現できます。
\begin{align}
d(a, b)&=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+\cdots +(b_n-a_n)^2} \\ &=\sqrt{\sum_{i=1}^{n} (b_i-a_i)^2} \\ &=\sqrt{\sum_{i=1}^{n} (b_i^2-2a_ib_i+a_i^2)}
\end{align}
今回は直接ベクトル間の距離を計算するのではなく、特徴マップやcodebookの行列を構成するベクトル間の距離を計算することになります。
上記の図のように計算することで、特徴マップを構成する$i$番目の特徴ベクトルと、codebook内の$j$番目のベクトルとのユークリッド距離を計算することができます。
この部分の実装は以下になります。
# distance: d( z[N, D], e[D, K] ) --> [N, K]
distance = (
flatten.pow(2).sum(1, keepdim=True)
- 2 * flatten @ self.embed
+ self.embed.pow(2).sum(0, keepdim=True)
)
これで特徴マップとcodebookを構成する特徴ベクトルの全パターンの距離を計算することができました。
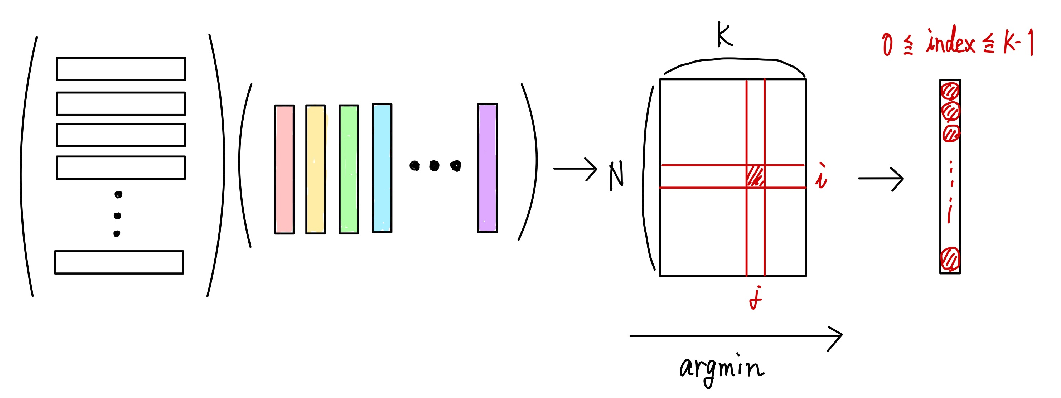
これでargminの引数の中身を計算することができました。次には以下のようにargminの計算を実行してインデックスを取得します。
k=\operatorname{argmin}_{j}\left\|\boldsymbol{h}-\boldsymbol{e}_{j}\right\|_{2}
実装は以下になります。
なお後続の処理のために計算されたインデックスを、入力された特徴マップのTensor形状に合わせて変換しています。
# minimum index: [N, K] --> [N, ]
embed_idx = torch.argmin(distance, dim=1)
# embed_idx: [N, ] --> [B, H, W, ]
embed_idx = embed_idx.view(input_shape[:-1])
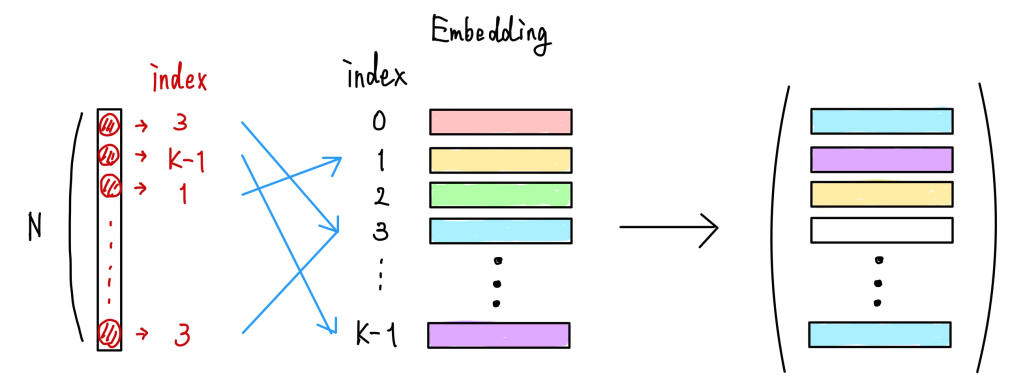
では得られたインデックスをもとに、codebook内のベクトルに変換していきます。これは合計で$B\times H\times W$個存在している特徴ベクトルを、codebook内の$K$個のベクトルに置き換える処理になります。
これはEmbedding層を使用することで以下のように計算できます。
実装は以下になります。
# quantize: [B, H, W, ] @ [K, D] --> [B, H, W, D]
quantize = F.embedding(embed_idx, self.embed.transpose(0, 1))
では実際に特徴マップとcodebookの学習を進めていく方法を考える。1つ考えることができるのは、以下のように互いの勾配計算を別途に行い、相互に特徴マップとcodebookが近づくように学習させていく方法です。
\mathcal{L}_{\mathrm{Q}}=\underbrace{\left\|\mathbf{s g}(\boldsymbol{h})-\boldsymbol{e}_{k}\right\|_{2}^{2}}_{\text {dictionary loss }}+\underbrace{\beta\left\|\mathbf{s g}\left(\boldsymbol{e}_{k}\right)-\boldsymbol{h}\right\|_{2}^{2}}_{\text {commitment loss }}
これは単純に以下のように実装することができます。
# loss
e_latent_loss = F.mse_loss(quantize.detach(), inputs)
q_latent_loss = F.mse_loss(quantize, inputs.detach())
loss = q_latent_loss + self.commitment * e_latent_loss
ここまでで入力から出力まで一連の計算を実施することができました。しかし、現状のままだと計算中にargminが存在しているため、勾配を伝搬させることができません。
そこでStraight Through Estimatorという考えを用いて、量子化した特徴マップから、入力された特徴マップに対してそのまま勾配を伝搬させるようにします。
実装では以下のようなテクニックを使用します。
quantize = inputs + (quantize - inputs).detach()
これで論文中で提案されていた内容のイメージと実装まで完了しました!
コードの全体像(クリックで展開)
class FeatureQuantizer(nn.Module):
r"""
Feature Quantization module.
https://github.com/YangNaruto/FQ-GAN/blob/master/FQ-BigGAN/vq_layer.py
Attributes:
emb_dim (int): Size of feature vector on dictionary.
num_emb (int): Number of feature vector on dictionary.
commitment (float): Strength of commitment loss. Defaults to 0.25.
"""
def __init__(self,
emb_dim,
num_emb,
commitment=0.25):
super().__init__()
self.emb_dim = emb_dim
self.num_emb = num_emb
self.commitment = commitment
self.embed = nn.Parameter(torch.randn(self.emb_dim, self.num_emb))
def forward(self, x):
r"""
Feature quantization feedforward function.
Args:
x (Tensor): Input feature map.
Returns:
Tensor: Output quantized feature map.
Tensor: Loss
Tensor: Embedding index for reference of shape [B, H, W]
"""
# x: [B, C=D, H, W] --> [B, H, W, C=D]
x = x.permute(0, 2, 3, 1).contiguous()
input_shape = x.size()
# flatten: [B, H, W, D] --> [N(=B x H x W), D]
flatten = x.view(-1, self.emb_dim)
# distance: d(flatten[N, D], embed[D, K]) --> [N, K]
distance = (
flatten.pow(2).sum(dim=1, keepdim=True)
- 2 * flatten @ self.embed
+ self.embed.pow(2).sum(dim=0, keepdim=True)
)
# embed_idx: [N, K] --> [N, ]
embed_idx = torch.argmin(distance, dim=1)
# embed_idx: [N, ] --> [B, H, W, ]
embed_idx = embed_idx.view(input_shape[:-1])
# quantize: [B, H, W, ] embed [K, D] --> [B, H, W, D]
quantize = F.embedding(embed_idx, self.embed.transpose(0, 1))
# loss
e_latent_loss = F.mse_loss(quantize.detach(), x)
q_latent_loss = F.mse_loss(quantize, x.detach())
loss = q_latent_loss + self.commitment * e_latent_loss
# straight through estimator
quantize = x + (quantize - x).detach()
# quantize: [B, H, W, D] --> [B, D, H, W]
quantize = quantize.permute(0, 3, 1, 2).contiguous()
return quantize, loss, embed_idx
def extra_repr(self):
return "emb_dim={}, num_emb={}, commitment={}".format(
self.emb_dim, self.num_emb, self.commitment
)
Disctionary Learning
$B\times H\times W$個存在している特徴ベクトルの集合に対して、最適なcodebookとは何かを考えると、最近傍法と同様に特徴ベクトルの平均で計算することができます。
e_i=\dfrac{1}{n_i} \sum_{j}^{n_i} z_{i,j}
しかしミニバッチを使って学習を行う勾配降下法では、多数存在している特徴ベクトルの平均を計算することは非常に難しくなります。
指数移動平均(EMA:exponentially moving average)
こうしたcodebbokのようなベクトル量子化用の重みを学習させる方法として、上記のような単純な平均を使用する方法以外に、 指数移動平均(EMA:exponentially moving average) を活用してオンラインで学習させる方法が存在しています。
この手法はMomentum Contrast for Unsupervised Visual Representation Learningのような自己教師あり学習でも使用されているテクニックになります。
これは数式で表現すると以下のようになります。
codebook内に存在する各ベクトルへの参照回数を計算し、参照回数で正規化することで最終的なベクトルを計算することができ、パラメータ$\gamma$を設定することで、どの程度過去の学習結果を反映させるのか決めることができます。
N_{i}^{(t)}:=N_{i}^{(t-1)} * \gamma+n_{i}^{(t)}(1-\gamma) \\
m_{i}^{(t)}:=m_{i}^{(t-1)} * \gamma+\sum_{j} z_{i, j}^{(t)}(1-\gamma) \\
e_{i}^{(t)}:=\dfrac{m_{i}^{(t)}}{N_{i}^{(t)}}
この数式も一見しただけでは、具体的な実装イメージを掴むことが難しかったです。そこで図示をもとにどのように計算すればいいのか明らかにしていきましょう。
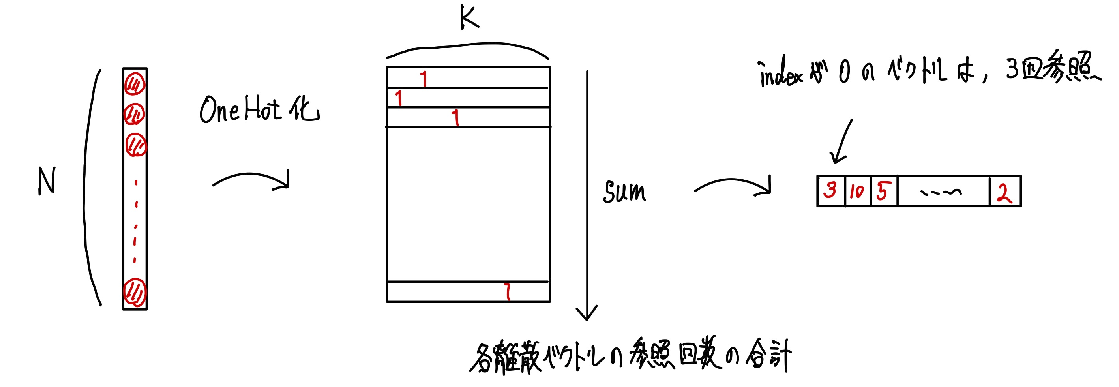
まずはcodebook内の各ベクトルに対する参照回数を計算します。これはベクトルに対するインデックスをOnehot化させて、特徴ベクトルの数で合計を計算すれば求めることができます。
あとは数式にしたがって、参照回数の指数移動平均を計算します。
N_{i}^{(t)}:=N_{i}^{(t-1)} * \gamma+n_{i}^{(t)}(1-\gamma)
# ref_count: [N, K] --> [K, ]
ref_count = torch.sum(embed_onehot, dim=0)
# ema for reference count: [K, ] by N = decay * N + (1 - decay) * n
self.cluster_size.data.mul_(self.decay).add_(
ref_count, alpha=(1 - self.decay)
)
数式を見るとわかるように、最終的にはcodebookのベクトルを指数移動平均を計算した後で、各ベクトルの参照回数で正規化をしています。
この際に、参照回数が0回のベクトルが存在していると.0で割り算をしてしまうことになってしまうため、Naive Bayesでも使用されているラプラス平滑化を使用します。
# total reference count
n = self.cluster_size.sum()
# additive (or, laplace) smoothing
smoothing_cluster_size = n * (
(self.cluster_size + self.eps) / (n + self.cluster_size * self.eps)
)
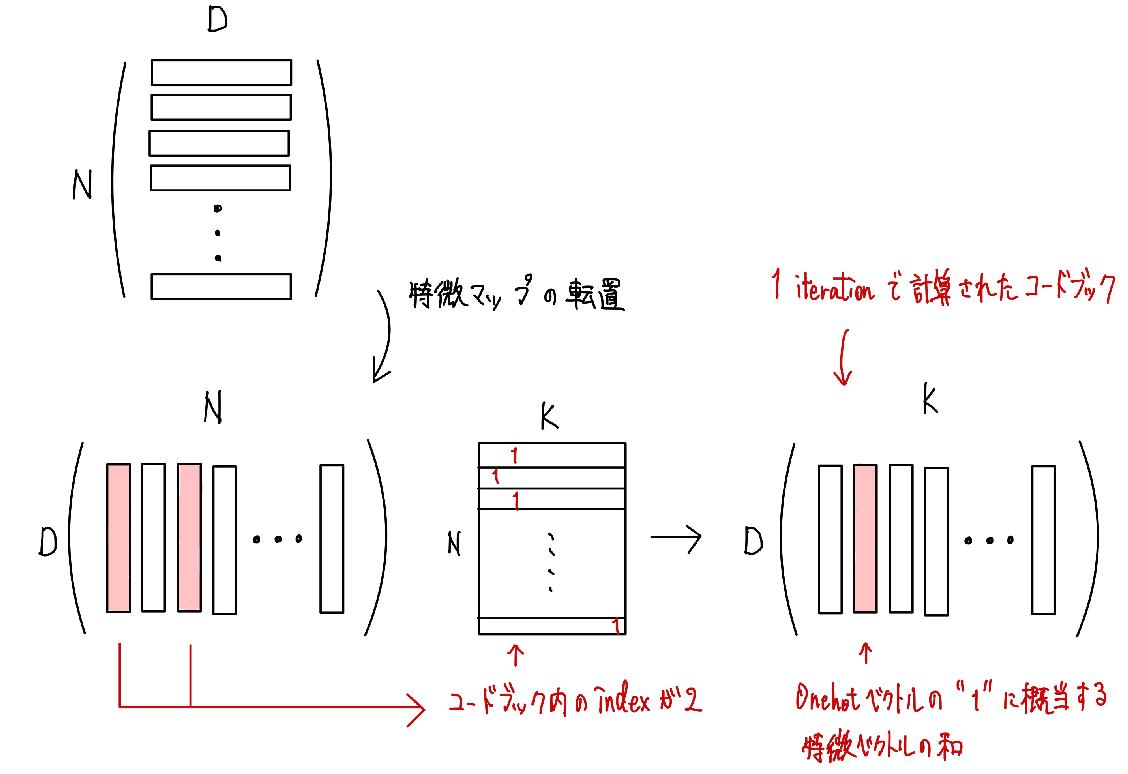
では次に学習中のミニバッチをもとにcodebook内のベクトル更新を計算します。ミニバッチ内の特徴ベクトルの平均を計算する際は、Onehot化させているインデックスと、入力された特徴マップから、同じベクトルを参照しているベクトル同士の合計を計算します。
実装は以下のようになります。
# dw: [D, N] @ [N, K] --> [D, K]
dw = flatten.transpose(0, 1) @ embed_onehot
あとは上記で計算したcodebook内のベクトルの更新量に対して、指数移動平均を計算すれば完了です。
m_{i}^{(t)}:=m_{i}^{(t-1)} * \gamma+\sum_{j} z_{i, j}^{(t)}(1-\gamma) \\
e_{i}^{(t)}:=\dfrac{m_{i}^{(t)}}{N_{i}^{(t)}}
# ema for embedding: [D, K]
self.ema_embed.data.mul_(self.decay).add_(dw, alpha=(1 - self.decay))
# normalize: [D, K] / [1, K]
embed_norm = self.ema_embed / smoothing_cluster_size.unsqueeze(0)
# update codebook
self.embed.data.copy_(embed_norm)
これで論文中で提案されていた指数移動平均を活用して計算のイメージと実装まで完了しました!
コードの全体像(クリックで展開)
class FeatureQuantizerEMA(nn.Module):
"""
Feature Quantization modules using exponential moving average.
This modules follow the equation (8) in the original paper.
https://github.com/YangNaruto/FQ-GAN/blob/master/FQ-BigGAN/vq_layer.py
Args:
emb_dim (int): Size of feature vector on dictionary.
num_emb (int): Number of feature vector on dictionary.
commitment (float): Strength of commitment loss. Defaults to 0.25.
decay (float, optional): Moment coefficient. Defaults to 0.9.
eps (float, optional): sufficient small value to avoid dividing by zero. Defaults to 1e-5.
"""
def __init__(self,
emb_dim,
num_emb,
commitment=0.25,
decay=0.9,
eps=1e-5):
super().__init__()
self.emb_dim = emb_dim
self.num_emb = num_emb
self.commitment = commitment
self.decay = decay
self.eps = eps
embed = torch.randn(self.emb_dim, self.num_emb)
self.register_buffer("embed", embed)
self.register_buffer("cluster_size", torch.zeros(self.num_emb))
self.register_buffer("ema_embed", embed.clone())
def forward(self, x):
r"""
Feature quantization feedforward function.
Args:
x (Tensor): Input feature map.
Returns:
Tensor: Output quantized feature map.
Tensor: Loss
Tensor: Embedding index for reference of shape [B, H, W]
"""
# x: [B, C=D, H, W] --> [B, H, W, C=D]
x = x.permute(0, 2, 3, 1).contiguous()
input_shape = x.size()
# flatten: [B, H, W, D] --> [N(=B x H x W), D]
flatten = x.view(-1, self.emb_dim)
# distance: d(flatten[N, D], embed[D, K]) --> [N, K]
distance = (
flatten.pow(2).sum(dim=1, keepdim=True)
- 2 * flatten @ self.embed
+ self.embed.pow(2).sum(dim=0, keepdim=True)
)
# embed_idx: [N, K] --> [N, ]
embed_idx = torch.argmin(distance, dim=1)
# set onehot label: [N, ] --> [N, K]
embed_onehot = F.one_hot(embed_idx, num_classes=self.num_emb).type(flatten.dtype)
# embed_idx: [N, ] --> [B, H, W, ]
embed_idx = embed_idx.view(input_shape[:-1])
# quantize: [B, H, W, ] embed [K, D] --> [B, H, W, D]
quantize = F.embedding(embed_idx, self.embed.transpose(0, 1))
# train embedding vector only when model.train(), not model.eval()
if self.training:
# ref_count: [N, K] --> [K, ]
ref_count = torch.sum(embed_onehot, dim=0)
# ema for reference count: [K, ] by N = decay * N + (1 - decay) * n
self.cluster_size.data.mul_(self.decay).add_(
ref_count, alpha=1 - self.decay
)
# total reference count
n = self.cluster_size.sum()
# additive (or, laplace) smoothing
smoothing_cluster_size = n * (
(self.cluster_size + self.eps) / (n + self.cluster_size * self.eps)
)
# dw: [D, N] @ [N, K]
dw = flatten.transpose(0, 1) @ embed_onehot
# ema for embedding: [D, K]
self.ema_embed.data.mul_(self.decay).add_(dw, alpha=(1 - self.decay))
# normalize: [D, K] / [1, K] --> [K, ]
embed_norm = self.ema_embed / smoothing_cluster_size.unsqueeze(0)
# embed = self.ema_embed / self.cluster_size.unsqueeze(0)
self.embed.data.copy_(embed_norm)
# loss
e_latent_loss = F.mse_loss(quantize.detach(), x)
loss = self.commitment * e_latent_loss
# straight through estimator
quantize = x + (quantize - x).detach()
# quantize: [B, H, W, D] --> [B, D, H, W]
quantize = quantize.permute(0, 3, 1, 2).contiguous()
return quantize, loss, embed_idx
def extra_repr(self):
return "emb_dim={}, num_emb={}, commitment={}, decay={}, eps={}".format(
self.emb_dim, self.num_emb, self.commitment, self.decay, self.eps
)
実験結果
では簡単に論文中の実験結果を見ていきましょう。
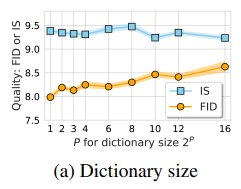
まずcodebook内に定義するベクトルの数を変化させた場合のFIDを見ていきましょう。$P$を増大させるとベクトル量子化の効果が小さくなり、導入前のモデルの性能に近づいていることがわかり、$K\rightarrow \infty$になるともとのモデルと全く同じ性能になると考えられます。
興味深い点はcodebook内のベクトルの数がたった2つしか存在しない場合で最も低いFIDを達成していることです。
(ISは高い値ほどよく、FIDは低い値ほどいい。)
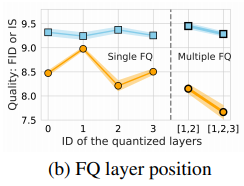
ベクトル量子化は複数の層に導入することで、より低いFIDを達成することができています。
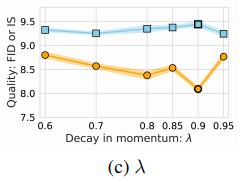
次に指数移動平均を計算する際の$\lambda$の値を変化させた場合の結果を見てみましょう。$\lambda$が大きければ、より過去の値を参照することになりますが、実験結果からは傾向は掴むことはできません。
ここらへんはデータセットに依存する気もします。
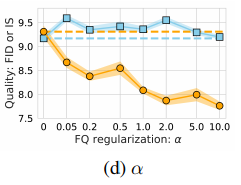
損失関数におけるベクトル量子化の重みの影響も見てみましょう。よりベクトル量子化の損失に重みを与えることで、低いFIDを達成できていることがわかります。
次に本手法をCifar10とCifar100に適用した場合の結果も見てみると、どちらの場合においてもFIDとISの両方を改善することができています。
| Cifar10 | Cifar100 |
|---|---|
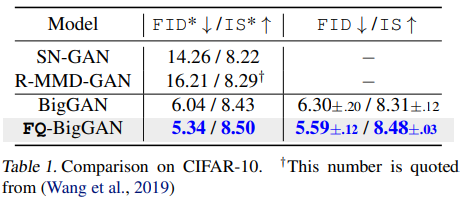 |
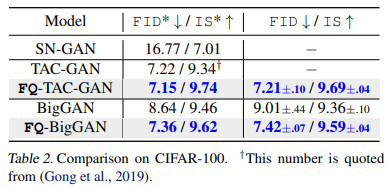 |
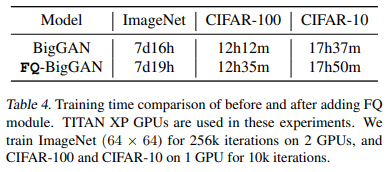
本手法は手軽にモデルに導入することができる手法でありながら、以下に示すように計算時間に大きな影響を与えることなく、性能を改善することができています。
また最終的なFIDとISを改善できているだけではなく、以下に示すように、学習のより早い段階でFIDとISの改善ができていることがわかります。
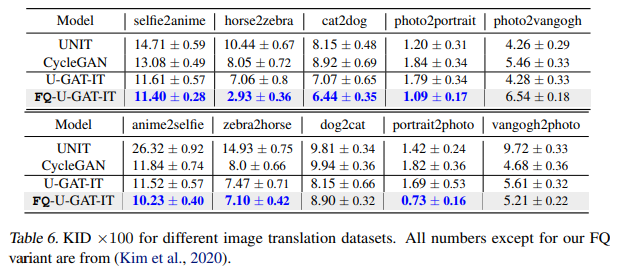
また画像生成だけではなく、スタイル変換にも適用することができ、ほとんどすべてのデータセットで性能を改善することができているます。
まとめと所感
自分自身の理解を可視化しながら論文を読み進めることで、論文から再現実装のイメージまで掴むことができました。
最近は業務で非常に忙しいため、論文に記載されていない内容であり、試したいと考えていた実験(バッチサイズの変更に対するFIDの変化など)ができていない点が残念なところ。
参考文献
- Yang Zhao, Chunyuan Li, Ping Yu, Jianfeng Gao, and Changyou Chen. Feature quantization improves gan
training. arXiv preprint arXiv:2004.02088, 2020 - Oord, A. v. d., Vinyals, O., and Kavukcuoglu, K. Neural discrete representation learning. In Advances in Neural Information Processing Systems, 2017.
- M. D. Zeiler and R. Fergus. Visualizing and understanding convolutional neural networks. In ECCV, 2014.
- A technical report on convolution arithmetic in the context of deep learning