累積和するときのメモ

累積和、理屈は分かってるけどとっさに実装できないよ

※「この記事は～」的な言い訳はめんどいので省略です。
正確な情報が必要な方は、ちゃんとした記事を参照ください。

要素数6個の配列で累積和を使うケースを考えます。

累積和用の配列は、元の配列より1つ長く、先頭は0にしておくのがポイント。

num[0]からnum[1]までの合計を求めるときは、sum[1+1] - num[0]する。
num[2]からnum[5]までの合計を求めるときは、sum[5+1] - num[2]する。

「まで」の方は+1

#define n (6)
int main() {
    int num[n] = {1,3,2,5,2,4};
    
    int sum[n+1];
    // 先頭を0にして
    sum[0] = 0;

    // 累積和を計算する
    for (int i = 0; i < n ; i++) {
    	sum[i+1] = sum[i] + num[i];
    }

    // 3～5の合計を求めるときは、(5+1までの和) - (3までの和)
    printf("%d\n", sum[5 + 1]-sum[3]);
	return 0;
}

exclusive_scan というのもある。

#include <numeric>
#define n (6)

int main() {
    vector<int> num = {1,3,2,5,2,4};

    // 末尾に0をpushするのがポイント
    num.push_back(0);

    // exclusive_scan は領域を確保しないので。事前に。
    vector<int> sum(n+1);
    exclusive_scan(num.begin(), num.end(), sum.begin(), 0);

    // 3～5の合計を求めるときは、(5+1までの和) - (3までの和)
    printf("%d\n", sum[5 + 1]- sum[3]);
	return 0;
}

2次元配列の累積和

(0, 0)を左上の頂点にした長方形に含まれる和を求めます。

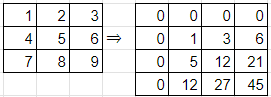
準備

たとえば(2,4)の27を求めるには、赤 + 青 - 黄 + (1, 2) ⇒ 12 + 12 - 5 + 8 = 27

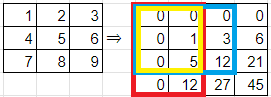
求める

たとえば赤の範囲を求めたいなら、緑 - 黄 - 桃 + 青 ⇒ 27 - 3 - 12 + 1 = 13

#define n (3)

int main() {
  int A[n][n] = {{1,2,3},
                 {4,5,6},
                 {7,8,9}};

  int sum[n + 1][n + 1];
  memset(sum, 0, sizeof(sum));

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + A[i][j];
    }
  }
  // 左上(1,1), 右下(1,2) の和を求める
  int lu_x = 0; int lu_y = 1; // 左上
  int rd_x = 1; int rd_y = 2; // 右下
  printf("%d - %d - %d + %d\n", sum[rd_y +1][rd_x +1] , sum[lu_y][rd_x +1] , sum[rd_y +1][lu_x] , sum[lu_y][lu_x]);
  printf("%d\n",                sum[rd_y +1][rd_x +1] - sum[lu_y][rd_x +1] - sum[rd_y +1][lu_x] + sum[lu_y][lu_x]);

  return 0;
}

正直、2次元の累積和は好きではないので、計算量が許されるなら行ごとに1次元の累積和したい。。。