1. はじめに
bitDPの解説読んだけど、「全体集合」「状態」「[S]」「O(N2^N)」とかむずかしい言葉ばかりで理解できないよ~![]()
となった方、いませんか?私がそうです。
私の理解力が足りないからです。数学の知識も足りていません。
これを書いている現在も、分かっていません。
ただ、なんとかbitDPの使い方は分かりましたので、記事を投稿します。
bitDPについて学びたかったけれど、難しい用語ばかりで理解できなかった…![]()
という人の助けになれば幸いです。
DP(動的計画法)は理解していることが前提です
2. bitで状態を表す
たいていのbitDP解説記事はまずこれから始まっていると思います。
で、これは多分つまづきポイントではないかと思いますが、一応。
「bitで状態を表す」際には、値を2進数で考えます。
そして、各ビットにそれぞれなんらかの意味を持たせます。
#define MAHI 0b00000000000000000000000000001000 // まひ
#define DOKU 0b00000000000000000000000000000100 // どく
#define YAKEDO 0b00000000000000000000000000000010 // やけど
#define NEMURI 0b00000000000000000000000000000001 // ねむり
int main() {
int status;
cin >> status;
if (status & MAHI) { // まひ判定
// まひ時処理
上記のように各ビットに意味を持たせることで、複数の状態をひとつの値に持たせることができます。
もちろん、それぞれの状態をbool値で管理することもできます。
ですが、『複数の状態をひとつの値に持たせる』ことがDPを行ううえで重要になります。
3. 『状態集合を添え字にとして持つDP』
これは、私がなんとかbitDPの理解に至った言葉です。
まあ、いまだ『状態集合』がいまいち分かっていませんが…
DP(動的計画法)の典型的な問題であるナップサック問題では、重さを添え字にします。
ナップサック問題では、例えば下記のケースで
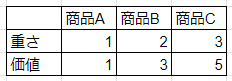
総重量 i の時にとり得る最大の価値 dp[i] を求めるには、
・ dp[i-1] + 1
・ dp[i-2] + 3
・ dp[i-3] + 5
のうち最大の価値になるものを選びます。
以下、4桁の数字は2進数です。0bってつけると見にくいので…
一方、bitDPでは『複数の状態をもたせた値』を添え字にします。
たとえば状態 1101 の時にとり得る最適値 dp[1101]を求めるには、
・ dp[0101] に 1000 を追加したもの
・ dp[1001] に 0100 を追加したもの
・ dp[1100] に 0001 を追加したもの
のうち最適になるものを選びます。
4. 例題
4つの食料があります。1日1つずつ食べます。
食料は食べた日によって満足度が異なります。
(一晩寝かせたカレーがおいしいとか、新鮮な魚はおいしいとか、そういう感じです)
全て食べ終わった時の最大合計満足度を求めなさい。

まず、それぞれの食料を食べたかどうかを、各ビットにアサインします。
食料0: 0001
食料1: 0010
食料2: 0100
食料3: 1000
食料0,1,2を食べ終わった状態は 0111 で表すことができます。
3日目までに食料0,1,2を食べ終わった場合の合計満足度の最大値 dp[0111] は
・dp[0110] + 3 (3日目に食料0を食べた)
・dp[0101] + 1 (3日目に食料1を食べた)
・dp[0011] + 2 (3日目に食料2を食べた)
のうち、最大のものになります。
実装はこんなかんじです。
#include <iostream>
#include <vector>
#include <bitset>
using namespace std;
int main() {
int N = 4;
// 食料の満足度[食料i][j日目]
vector<vector<int>> food{{1,3,3,4},{2,1,1,1},{1,3,2,2},{3,2,1,1}};
vector<int> dp((1 << N), 0);
// 0001 から 1111 までまわす
for (int i = 1; i < (1 << N); i++) {
for (int j = 0; j < N; j++) {
int x = 1 << j;
// 0001, 0010, 0100, 1000 のうち、i のビットが立っているものについて
if (i & x) {
// 何日目かを知るために、立っているビットを数える
int day = bitset<16>(i ^ x).count();
// dp[0111] は、下記のうち最大のもの
// ・dp[0110] + 食料[0][3日目]
// ・dp[0101] + 食料[1][3日目]
// ・dp[0011] + 食料[2][3日目]
dp[i] = max(dp[i], dp[i ^ x] + food[j][day]);
}
}
}
cout << dp.back() << endl;
// debug
for (int i = 1; i < (1 << N); i++) {
cout << bitset<4>(i) << ":" << dp[i] << endl;
}
return 0;
}
(1 << N) というのが、普段あまり見ない表記ですね。
上記のケースでは0001から1111までのdpを埋めたいので、forの上限を10000にしている、ということです。
(i ^ x) も普段あまり見ない表記ですね。
^ は排他的論理和で、意図としては i から x のビットを落とす、というものです。
i = 0111, x = 0001 なら i ^ x は 0110 になります。
実行結果は下記の通りです。
食料を3, 2, 1, 0 の順で食べると、合計満足度の最大値は11になります。
また、デバッグ情報としてdpの中身をすべて出してみました。
例えば 1001:6 は、2日目までに食料0と食料3を食べた時の合計満足度の最大値が6であることを示します。
11
0001:1
0010:2
0011:5
0100:1
0101:4
0110:5
0111:8
1000:3
1001:6
1010:4
1011:7
1100:6
1101:9
1110:7
1111:11
5. 計算量
例題のようにN=4であれば4!=24通りの組み合わせすべてを求めてることもできますが、
N=16となると16!=20,922,789,888,000通りと膨大な量になってしまいます。
そこで上記のようにbitDPを使用すると、
N=4なら(2^4)×4 = 64 回のループで、N=16でも(2^16)×16 = 1,048,576 回のループで済みます。
ここまで書いて、ようやくO(N2^N) の意味が分かりました。
// 0001 から 1111 までまわす
for (int i = 1; i < (1 << N); i++) { // ここが 2^Nで
for (int j = 0; j < N; j++) { // ここがN
だったんですね。
6. 応用
巡回セールスマン問題
巡回セールスマン問題とは、N個の地点をすべて1回ずつ巡回する場合の最短経路を求める問題です。
巡回済みの場所をビット管理するのですが、追加情報として、直前に巡回した場所が必要になるので、
2次元の動的計画法ということになります。
例えば『地点0,1,2が巡回済み、最後に巡回した場所が2』の dp[0111][2] の最適値は、
・dp[0011][0] + 地点0->2の距離
・dp[0011][1] + 地点1->2の距離
のうち、最適な方となります。
巡回セールスマン問題は、巡回する場所の順列の問題ではありますが、
1つビットを立てるためには「1つ前に立てたビットがなにか」を知る必要がある、
ちょっとした応用問題になるかと思います。
n個の中から2個のペアを作れるだけ作って最適を求める
n個のアイテム A, B, C, D, ... があり、AとBのペアなら1ポイント、AとCのペアなら2ポイント、
のように各組合せにポイントが設定されており、最大値をめざすというものです。
(AtCoder ABC318 D問題)
DCBAの順にビットをアサインし、ペアとして選択済みのビットを立てることにすると、
dp[1111] は
・dp[1100] + A-Bペアのポイント
・dp[1010] + A-Cペアのポイント
・dp[0110] + A-Dペアのポイント
・dp[1001] + B-Cペアのポイント
・dp[0101] + B-Dペアのポイント
・dp[0011] + C-Dペアのポイント
のうち最大のものになります。
ただ、A-B選択済みのところにC-Dのポイントを足すことと、
C-D選択済みのところにA-Bのポイントを足すことは、結果的に同じになります。
よって、実は下記の3通りだけ検討すればよいということになります。
・dp[1100] + A-Bペアのポイント
・dp[1010] + A-Cペアのポイント
・dp[0110] + A-Dペアのポイント
これを端的に言うと
「追加する2つのビットのうち1つを、最下位ビットに固定できる」
ということになるようです。
dp[]が加算されるのが2個おき、追加するビットを固定できる、というのが応用ポイントですね。
7. 最後に
私がbitDPをなかなか理解できなかったのは、最初にbitDPに触れたのが
「n個の中から2個のペアを作れるだけ作って最適を求める」
だったためです。。。
いきなり応用から入ってはダメですね…。
あとは
dp[0110]はどうやって求めるのか?
というのがなかなか理解できなかった、というのがあります。
この投稿ではできるだけ簡単な例で、dp[]の求め方が分かりやすいように、
難しい言葉をできるだけ使わずに、書いてみました。