概要
「3種類の文字だけで無限長さの『繰り返しのないの文字列』を作れるか?」という問いについて考えました。(「繰り返し」は次節で説明するこの問題独自の定義です)
証明できていませんが、一定程度の長さ(10000)までは繰り返しのない数列が作れることをプログラムで確認しました。
繰り返しのある/ない文字列
ある文字列のなかに同一の部分文字列(長さ1以上)が隣り合って存在しているとき、その文字列は繰り返しのある文字列であるとします。
繰り返しのある文字列の例を示します。(繰り返し部分を太字にしています)
- abcbca
- aab
- abcdefbcdbcdabcd
逆にある文字列が繰り返しのある文字列でない時、繰り返しのない文字列とします。繰り返しのない文字列の例を示します。
- aba
- abcbac
- abcdabce
同じ部分文字列が登場していても隣り合っていない場合は繰り返しのない文字列となることに注意してください。
使える文字の種類が限られるとき、繰り返しのない文字列はどのくらいの長さまで作れるか?
使える文字が1種類のとき
使える文字列が1種類(例えば"a")のとき、繰り返しのない文字列は何文字の長さまで作ることができるでしょうか?
長さ1のとき、以下のように繰り返しのない文字列を作ることができます
- a
長さが2のとき、繰り返しのない文字列を作ることはできません。具体的には、1種類の文字を使って作れる長さ2の文字列は"aa"のみですが、これは繰り返しのある文字列です。
よって、使える文字が1種類のとき、繰り返しのない文字列を作れる最大長さは1です。
使える文字が2種類のとき
使える文字列が2種類(例えば"a","b")のとき、繰り返しのない文字列は何文字の長さまで作ることができるでしょうか?
長さ1のとき、以下のように繰り返しのない文字列を作ることができます。
- a
長さ2のとき、以下のように繰り返しのない文字列を作ることができます。
- ab
長さ3のとき、以下のように繰り返しのない文字列を作ることができます。
- aba
長さ4のとき、繰り返しのない文字列を作ることはできません。具体的には2種類の文字で作れる長さ4の文字列は"aaaa","aaab","aaba","aabb","abaa","abab","abba","abbb"および、これの"a"と"b"を入れ替えたものですが、これらはすべて繰り返しを含みます。
よって、使える文字が2種類のとき、繰り返しのない文字列を作れる最大長さは3です。
使える文字が3種類のとき
使える文字列が3種類(例えば"a","b","c")のとき、繰り返しのない文字列は何文字の長さまで作ることができるでしょうか?
地道に手を動かしてみると、少なくとも長さ10までは以下のように繰り返しのない文字列を作れることがわかります。
| 長さ | 繰り返しのない文字列の例 |
|---|---|
| 1 | a |
| 2 | ab |
| 3 | aba |
| 4 | abac |
| 5 | abacb |
| 6 | abacba |
| 7 | abacbab |
| 8 | abacbabc |
| 9 | abacbabca |
| 10 | abacbabcab |
なんだかこの調子でいくらでも長く、繰り返しのない文字列を作れそうです。
本当でしょうか? 以下、3種類の文字が使える場合についてもう少し考えてみます。
文字列長を固定したときに繰り返しのない文字列を何通り作れるか
3種類の文字が使えるときに繰り返しのない文字列を無限に作れるか?という問いの答えを直接的に証明することは難しかったです。(有名な問題だったりするのでしょうか? だれか知っていたら教えてほしいです)
そこで、とりあえず文字列長Lのときに、繰り返しのない文字列が何通り作れるか調べてグラフを書いてみることにしました。
繰り返しのある文字列の判定
準備として、ある文字列が繰り返しを含むかどうかを判定する関数を作ります。
pythonの場合、隣り合う同じ長さの部分文字列は整数$i,j$を用いて、
text[j:j+i], text[j+i:j+2*i]のように書けます。
ただし、$i$は部分文字列の長さ、$j$は一番左の文字のindexを0としたときの左側の部分文字列の開始位置のindexです。
あとは$i,j$の取りうる範囲をループで回して、この部分文字列の異同を判定すればよいです。
与えられた文字列の長さをLとすると、$i,j$の取りうる範囲は
$1\leq i \leq L/2$
$0\leq j \leq L-2i$
です。
$i,j$をこれらの範囲で動かして、text[j:j+i]とtext[j+i:j+2*i]を比較すれば、ある文字列が繰り返しを含むかどうかがわかります。
# textが繰り返しを含むときTrueを返し、含まないときFalseを返す
def is_repeat(text):
for i in range(1,len(text)//2+1):
for j in range(len(text)-2*i+1):
if text[j:j+i]==text[j+i:j+2*i]:
#print(j,j+i,text[j:j+i])
return True
return False
ただ、上記関数の計算量はざっくり$O(L^2)$で、ちょっと多いです。
文字列Aが繰り返しのない文字列であるとき、Aの端に一文字足したA'の繰り返し判定は、少ない計算量で行えます。足した1文字を含む部分文字列についてだけ検討すれば良いので、計算量は$O(L)$です。
def is_added_text_repeat(text,char):
text = char + text
for i in range(1,len(text)//2+1):
if text[:i]==text[i:2*i]:
return True
return False
次小節で説明するように、繰り返しのない文字列を生成するときには、既知の繰り返しのない文字列に1文字ずつ足すという操作をするので、こちらの判定方法が使えます。
1文字ずつ追加しながら繰り返しのない文字列かどうかを判定する
文字列長Lと繰り返しのない文字列の個数の関係を調べるために、繰り返しのない文字列を総当りで作っていきます。
これは既知の繰り返しのない文字列の端(プログラムでは先頭)に、1文字足したものが、繰り返しを含むかどうかを調べる、ということを順次行うことで達成されます。(1度繰り返しが生じると、以降何文字足しても繰り返しを含むままなので、繰り返しのある文字列に1文字足したものを考える必要はありません)
Lが少ないものから優先的に生成したいので、幅優先探索で実装します。
また、初期値は"ab"に固定しており、文字の入れ替えによる重複を無視しています(つまり実際の個数はこれの6倍です)。
from collections import deque
# lengthの長さまでの繰り返しのない文字列の個数を出力する
def without_repeat_text_bfs(length):
unit = ["a","b","c"]
q = deque(["ab"])
cnt = {2:1}
prev = "ab"
while q:
tmp = q.popleft()
if len(tmp) > len(prev):
print(len(prev),cnt.get(len(prev),0))
prev = tmp
if len(prev) >= length: continue
for u in unit:
if prev[0] == u: continue
if is_added_text_repeat(prev,u): continue
l = len(prev)+1
cnt[l] = cnt.get(l,0)+1
q.append(u+prev)
print(length, cnt.get(length,0))
出力は下記のような感じです。
>>>without_repeat_text_bfs(55)
2 1
3 2
4 3
5 5
6 7
7 10
8 13
9 18
10 24
...
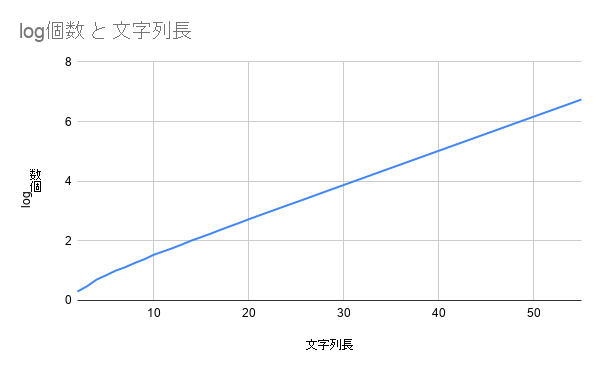
L=55までの繰り返しのない文字列の個数をグラフにしたものが以下です。

ほぼ直線になったのでどうやら指数関数的に増加するようです。
これがどこかで急に0になるということは考えにくいので、Lがどんなに大きくても、繰り返しのない文字列を作ることができそうです(証明されたわけではありません)。
繰り返しのない文字列が作れることを何文字まで確定できるか?
無限に作れそうだ、とはいってもL=55までだとさすがに少ない気がするので、もう少し大きいLまで、少なくとも1つは繰り返しのない文字列があることを確認しようと思います。
前節の関数で、個数を愚直に求めると計算時間がかかりすぎるのですが、少なくとも1個見つけるだけであれば、深さ優先探索によって、もう少し効率的に計算できそうです。
def without_repeat_text_dfs(length):
unit = ["a","b","c"]
q = deque(["ab"])
prev = ""
while q and len(prev) < length:
prev = q.pop()
for u in unit:
if prev[0] == u: continue
if is_added_text_repeat(prev,u): continue
#1文字足したテキストが繰り返しのない文字列だった時
#引数で指定した長さより生成した文字列が長ければ、関数を終了する
if len(u+prev) >= length:
return u+prev
#キューに新しい文字列を加える
q.append(u+prev)
上記関数を使って調べた結果、L=10000までは繰り返しのない文字列が見つかることを確認できました。
おわりに
繰り返しのある(ない)文字列というものを定義して、使える文字の種類が限られるときに、繰り返しのない文字列がどのくらいの長さまで作れるかを検証しました。
使える文字の種類が1種類、2種類のときは有限長さまでしか作れませんでした。3種類のときは、証明はできませんでしたが、グラフの形状から無限長さまで作れそうだということが推測できました。また、少なくとも長さ10000以下のときは繰り返しのない文字列が存在することが確かめられました。
(推測が正しいとして)1種類、2種類では有限なのに3種類になった瞬間に急に無限に発散するというのはちょっと興味深いです。あらゆる地図が4色あれば隣接する領域が同じ色にならないように塗り分けられるという、四色定理というものがありますが、関係していたりするのでしょうか?(単純に四色定理の1次元版、ということではないですが)。 というかすでに証明済みの問題だったりするのでしょうか? もしわかる方いたら情報いただけると嬉しいです。