機械学習で予測したり、分類したりという分析手法が大流行している中で数理最適化は今となってはかゆいところに手が届く技術です。一時期は強化学習があるからいらないんじゃないか、と考えたこともあったのですが、実用性を考えると即座に実装できたり、運用のしやすさといった点で数理最適化の強さが活きる局面はまだまだ多いでしょう。特に最近では量子コンピュータの実用化の研究がされており、もし普及した場合には間違いなく再注目される技術です。
今回は数理最適化をする上で知っておきたい定式化テクニックをまとめました。たぶん数式は間違ってないですが、もしかしたら間違っている可能性もあります。
論理積
バイナリ変数$x, y$の積は線形な式のみで$xy$と等価な式を作れます。
z \geq x + y - 1 \\
x \geq z \\
y \geq z \\
x, y, z \in \left\{0, 1\right\}
$x=1, y=1$のときのみ$z=1$でそれ以外のときは$z=0$になることがわかります。
論理和
$x \leq 2$または$y \leq 3$を満たす制約は以下で表せます。
x - 2 \leq Mz \\
y - 3 \leq M(1-z) \\
z \in \left\{0, 1\right\} \\
Mは大きな定数
右辺がMになった場合は実質その制約はないものと同じことになりますのでその場合はもう片方を必ず満たすように動いてくれます。$z$が0,1のいずれかになることで片方の制約が有効になるようなスイッチの役割を果たしています。
条件分岐
$y=1$のとき$x=0$になる制約を以下の式で表せます。
x \leq M(1 - y) \ \ \ \ Mは大きな定数 \\
x, y \in \left\{0, 1\right\}
$y=1$のときは右辺が0になるので$x=0$を限定し、$y=0$のときは$x$は0,1のいずれでも取れる自由な変数になります。
活用例ですが、例えばスケジューリングを想定したときに
M(1 - x_t) \geq x_{t+1} + x_{t+2} + x_{t+3} \\
x_t\in \left\{0, 1\right\}
の制約で時刻$t$に仕事を入れた場合、入れない場合の場合分けを記述できます。$x_t$の仕事が3単位時間かかるときに$x_t=1$になると$x_{t+1},x_{t+2},x_{t+3}$は仕事を入れられませんので0で縛れます。$x_t=0$の場合は後ろ3つは自由なので0,1の選択肢を与えられます。
m個のうちn個満たす
スイッチの応用で制約をmustな扱いからいくつか満たしていればよいという準制約な扱いに落とすこともできます。
$x_1 \leq 0, x_2 \leq 0,..., x_m \leq 0$のm個のうちn個満たす制約は大きな定数$M$を用いて以下のようにあらわせます。
x_k \leq M(1-y_k)\ \ \ \ \ \ for \ k = 1,...m \\
\sum_k^m y_k = n \\
y_k \in \left\{0, 1\right\} \ \ \ \ \ \ for \ k = 1,...m
$y=1$のときは$x \leq 0$となり、$y=0$のときは$x$は自由な変数となります。$y=1$となる個数を制約に加えることで$n$個満たす制約を表せます。少しの変更で$n$個以上満たす、という制約にしたり、目的関数に$y_k$項を加えることでできるだけ多く満たす、のように変形できます。業務で活用する場合に、どうしてもすべての要件(制約)を満たすことが難しい場合がありますが、そういうときに解なしで出力する手もありますが、できるだけ満たす解を出力するという手もあります。使い分けましょう。
隣り合う2つ
x_1 \leq y_1 \\
x_2 \leq y_1 + y_2 \\
x_3 \leq y_2 + y_3 \\
x_4 \leq y_3 \\
y_1 + y_2 + y_3 = 1 \\
y_1, y_2, y_3 \in \left\{0, 1\right\} \\
x_1, x_2, x_3, x_4 \geq 0
1になった$y$が含まれる式だけが右辺が1になり該当する2つのxが0から1の値をとることをでき、それ以外は0で縛ることができます。これはSOS制約(special ordered set)と呼ばれていて有名な式になります。
区分線形近似
青線の関数を赤線の区分線形関数と近似して、赤線上の点$(x,y)$を制約式で表します。
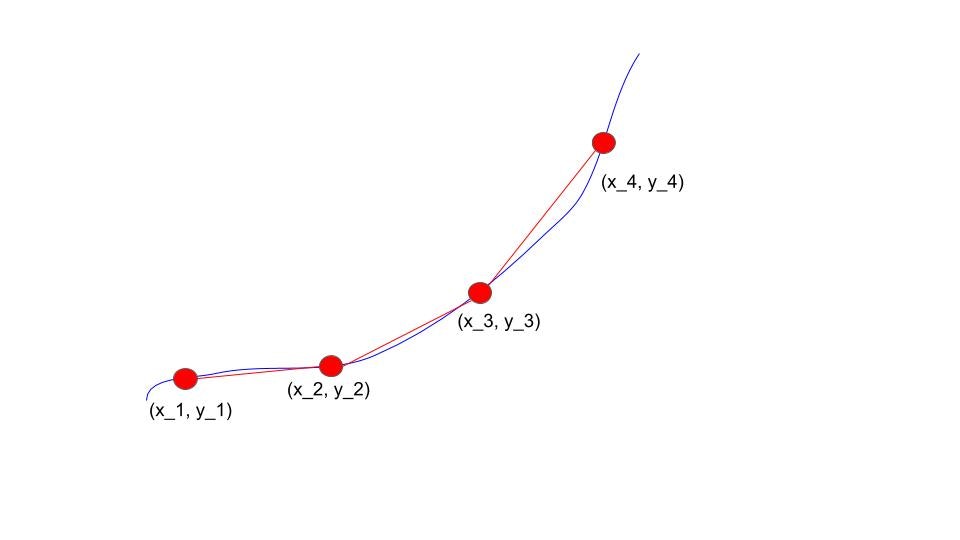
(x, y) = a_1 (x_1, y_2) + a_2(x_2, y_2) + a_3 (x_3, y_3) + a_4(x_4, y_4)\\
a_1 + a_2 + a_3 + a_4 = 1 \\
a_1 \leq b_1 \\
a_2 \leq b_1 + b_2 \\
a_3 \leq b_2 + b_3 \\
a_4 \leq b_3 \\
b_1 + b_2 + b_3 = 1 \\
b_1, b_2, b_3 \in \left\{0, 1\right\} \\
a_1, a_2, a_3, a_4 \geq 0
隣り合う2つの制約を応用することで実現できています。$a_1, a_2, a_3,a_4$の隣り合う2つの和が1になる制約になりますので、それはすなわち$(x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4)$のうち隣り合う2点の内分点を意味します。赤線上の点を表せました。
線形回帰
最適化モデリングでさまざまな線形回帰を実現できます。
$y=ax + b$でパラメータ$a,b$を求めたいときに誤差関数を定義して最小化します。
min \sum_{i}^{n}t_i \\
subject \ \ to: \\
y_i - (a x_i + b) \geq -t_i, \ \ for \ \ i = 1,..., n\\
y_i - (a x_i + b) \leq t_i, \ \ for \ \ i = 1,..., n\\
t_i \geq 0
これは$t_i = |y_i - (ax_i + b)|$で損失誤差を制約式で表したものになっています。最適化の定式化で誤差$t_i$を等式ではなく、不等式の制約にして問題ないかというと問題ありません。例えば$y_i - (ax_i + b)$の値が-2のとき、2つの制約式を満たす$t_i$は$t_i >= 2$となります。目的関数に$t_i$の総和を最小化するような設定になっていて、最適解では$t_i = 2$が成り立ちますので、それは損失誤差と一致することになります。これで線形回帰を記述できました。
線形回帰は自前で実装するという機会は少ないですが、最適化問題の定式化は柔軟な制約式を加えた回帰を可能にします。例えば、区分線形近似の例と合わせた区分線形回帰、パラメータ$a,b$に上下限を設定した回帰などは簡単に作れそうです。
株価データの分析では特殊な線形回帰としてsupport lineというものがあり、これも最適化問題を解くことで得られます。support lineは下図のチャートデータで青線で描かれた株価を支える底線のことです。
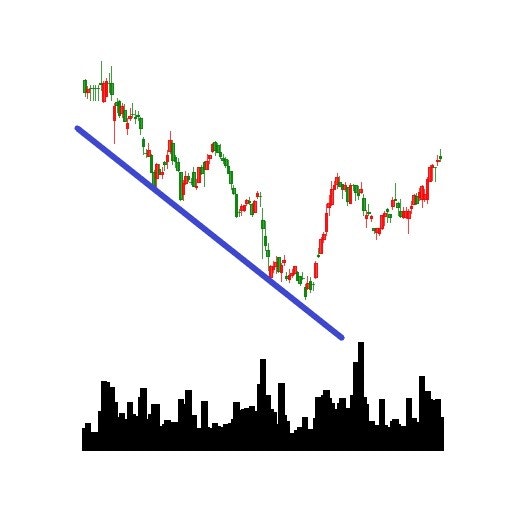
青線を計算するための最適化問題は以下で表せます。
min \sum_{i}^{n}(y_i - (ax_i + b))^2 \\
subject\ \ to: \\
y_i \geq (ax_i + b)
目的で損失関数を最小化しつつ、回帰直線がチャートデータよりも下になるような制約を設定して実現しています。
線形回帰ではないですが、SVMは制約付き最適化問題としての表現を確認するとSVMの理解がぐっと深まります。
業務での数理最適化活用
理論的な定式化方法を知っても慣れないと業務で活用するのは容易ではありません。教師データという形で正解を予測するようなタスクとは違い、業務そのものを理解し数式に落とし込んでいく必要があります。その業務をやっている人は数理最適化のことは当然わかりませんので双方の専門性を相互活用するようなチームワークの構築が重要です。
定式化テクニックそのものについては手っ取り早く勉強する方法はあんまりないと思っています。「こういう要件を数式にしたいけど検索の仕方がわからない」という事態に陥ることがあり、ニッチすぎてどうしようもないです。これに関してはあらかじめ最適化の応用系の論文をある程度読み込んでおくことで、どういう問題に対してどういう定式化を実装したかという事例を頭に入れておくくらいしかないんじゃないでしょうか。頭に入れたら自分で実際に使っていくことで要件⇔数式がスムーズに変換できるようになってきたような気がします。
教師あり学習と数理最適化の使い分け
教師あり学習と数理最適化をどのように使い分けるかというのは技術選択という点で難しいです。個人的な選択基準としてデータドリブンかどうかと正解データがわかるかどうかを目安にしています。データを蓄積してそれを活用してまた次のデータを生み出すというサイクルを作る場合は教師あり学習は有効ですが、そもそもデータがないという状態では教師あり学習はできませんのでデータが増えるまで待つか数理最適化で課題解決を試みるかという分岐が生まれます。データがあっても正解データがわからない、教師ラベルをつけにくいという場合には数理最適化の強みが活きるかもしれません。このとき強化学習やバンディットなどの別の手法も候補に上がりますが、選択肢を多く持っておくのは悪いことではないでしょう。