機械学習で株価予測や競馬予測のアルゴリズムを開発している人は多くないですが、興味ある人はそれなりにいると思います。Qiitaを検索すると機械学習手法の勉強のためにちょっと触ってみたという感じの人は結構見かけます。投資や競馬に興味がなくても、ルールが決まっていて、勝つというゴールがシンプルなため機械学習の勉強と相性が非常に高いですので、個人のスキルアップにもおすすめなテーマだと思っています。今回は株価の時系列予測に関連した技術を紹介します。
一般的な時系列データの類似度
時系列データの類似度というと、dynamic time warpingが王道な手法として思い浮かぶかと思います。DTWをQiitaで検索すると以下の記事に説明がありました。
DTW(Dynamic Time Warping)/動的時間伸縮法について話す
時系列同士の長さや周期が違っても類似度を求めることができます。
なので、DTWは「周期はずれているが、形は似ている」という場合や、系列同士の長さが異なるデータの類似度を測りたいときに他の手法よりも便利な手法だと言えます。
というのが特徴で株価分析において有効な手法です。
株式市場の動き
次に株式市場がどのように動いているかを考えます。参戦している人は少額の資産を運用する個人投資家(人間)と多額の資産を運用する機関投資家(アルゴリズム)に分けられ、個人投資家で億トレーダーになれるのは数えるほどです。億を目指すにはそれなりのリスクを背負った勝負をしなければならず、9割以上の人は負けると言われています。なぜかというと機関投資家の資金力と強力なアルゴリズムによってドカンとやられてしまうからです。アルゴリズムはまるで個人投資家(人間)の売買行動や心理を読んでいるかのような動きをするくらいに強いです。
本記事の趣旨
個人投資家がデータサイエンスを使って参戦するとしたらアプローチはいくつか考えられますが、今回は個人投資家(人間)の投資判断を学習するための技術に焦点を当てます。人間の行動を予測するために時系列データ間の類似度を計算したいのですがDTWは使いません。人間の行動を予測するために人間がプロットされた時系列データを見て直感的に感じる類似性を捉える必要があり、DTWよりもベターな方法を考えたいです。また、株価の時系列データは始値、高値、安値、終値、出来高の5つの時系列データによって構成されるためDTWで細かい解析は難しいです。人間が目で見た時の時系列データ類似度を視覚的類似度と呼ぶことにしてそれを計算する手法を紹介します。
計算手順の流れ
視覚的類似度を計算するまでの流れを以下の順で説明します。
- 時系列データを可視化する
- オートエンコーダーのディープラーニングで可視化した時系列データを学習させる
- エンコーダーの出力層で時系列データをベクトルデータに変換
- ベクトルデータ間の距離を定義して視覚的類似度を出力する
ここからは内容が複雑になってきますので結果だけ知りたい場合は以降の折り畳みを読み飛ばしましょう。なお、今回実装したコードは
https://github.com/shiibashi/qiita/tree/master/12
にあります。
1.時系列データを可視化する
時系列データの可視化手法については過去の記事でもとりあげています。mpl-financeを使えば簡単に生成できます。 [ローソクチャート画像を用いた株価の変動予測](https://qiita.com/shiibass/items/19ff37604cca8eac5939)2.オートエンコーダーのディープラーニングで可視化した時系列データを学習させる
オートエンコーダーの基本的な考え方は入力と出力が同じニューラルネットワークでエンコーダーでデータを圧縮してデコーダーで復元して元の入力と同じものを再現するというものです。教師ラベルが自身なのでアノテーションを必要としないのが強みです。よく用いられる事例としては異常検知やノイズ除去などになります。  今回はこのニューラルネットワークで中間データをベクトルになるようなネットワークを組みます。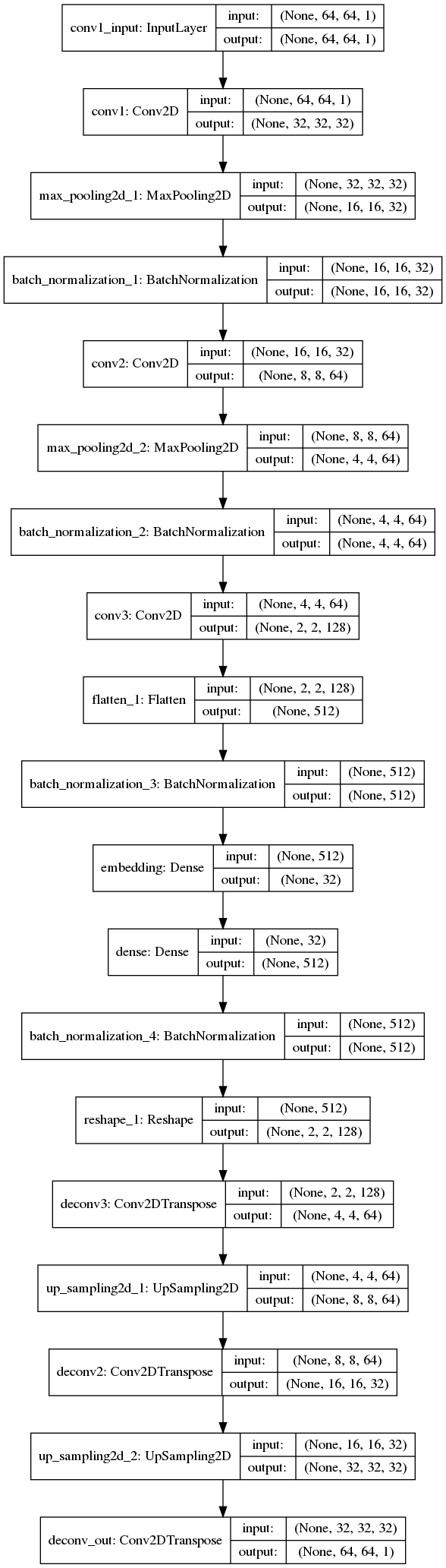
3.エンコーダーの出力層で時系列データをベクトルデータに変換
2.で学習したニューラルネットワーク全体を使うのではなくエンコーダーの部分のみを使います。↓の画像において中間層の出力結果を取得してデコーダーはもう使いません。 4. ベクトルデータ間の距離を定義して視覚的類似度を出力する
3でベクトルデータに変換したことで容易にベクトル間の距離を定義して類似度を計算できるようになりました。画像や時系列データだと距離の定義が困難であったり、データの長さが異なったりすると思うように類似度を計算できません。特に、今回開発したいのは視覚的な類似度なので今回の手順を採用しています。 類似度の計算はこちらのノートブックでコードを書きました。(L2ノルムの分子だけしか計算していません) https://github.com/shiibashi/qiita/blob/master/12/script/similarity_search_script.ipynb実験
日本の株価データを上記の方法で349000枚学習させました。githubには学習済みモデルは上げてありますが、元データはLIFULLのデータしか上げていません。githubには出来高付きの本格的なチャート画像で学習するコードも書いてありますのでデータを用意してもらえればより実用レベルの機械学習モデルを作れます。
学習したモデルを以下のようなスクリプトで特定の銘柄$c_{query}$の日時$t_{query}$におけるデータをクエリとして、$t_{query}$以前のデータで最も類似度の高い銘柄、日時$(c^*, t^*)$を検索します。いわゆる類似検索です。高速化を目指す場合は近似近傍探索を実装するのが望ましいです。
https://github.com/shiibashi/qiita/blob/master/12/script/similarity_search_script.ipynb
検証するものは以下の2つでいくつかサンプル結果を挙げます。
A: 2つの時系列データ$(c_{query}, t_{query})$と$(c^*, t^*)$が似てるかどうか
B: 2つの時系列の検知後1週間の動き($(c^*, t^*+7days)$の動きと$(c_{query}, t_{query}+7days)$の動き)がどうなるか(予測できるのか、関係性があるのか)
記事タイトルは類似度についてですが、その先にある目的は後者の予測をするということにありますので検証のメインはそちらです。比較は表形式にまとめて
| クエリ($c_{query}$), 日付($t_{query}$) | 検索結果$c^*, t^*$ | |
|---|---|---|
| 検証A(視覚的類似度検証) | 画像 | 画像 |
| 検証B(後1週間の動き検証) | 画像 | 画像 |
| のようにします。検証Bの画像では$t_{query}$と$t^*$の日付に縦の白い線を引きました。なのでその翌営業日以降の動きを比較することになります。 |
4592, サンバイオ
4連S安で株価が1/5になった話題の銘柄です。左(クエリ)と右(検索結果)で類似した時系列を取得できることに注目してください。
| 4592, サンバイオ, 2019-02-06 | 8912, エリアクエスト, 2018-02-16 | |
|---|---|---|
| A |  |
 |
| B | 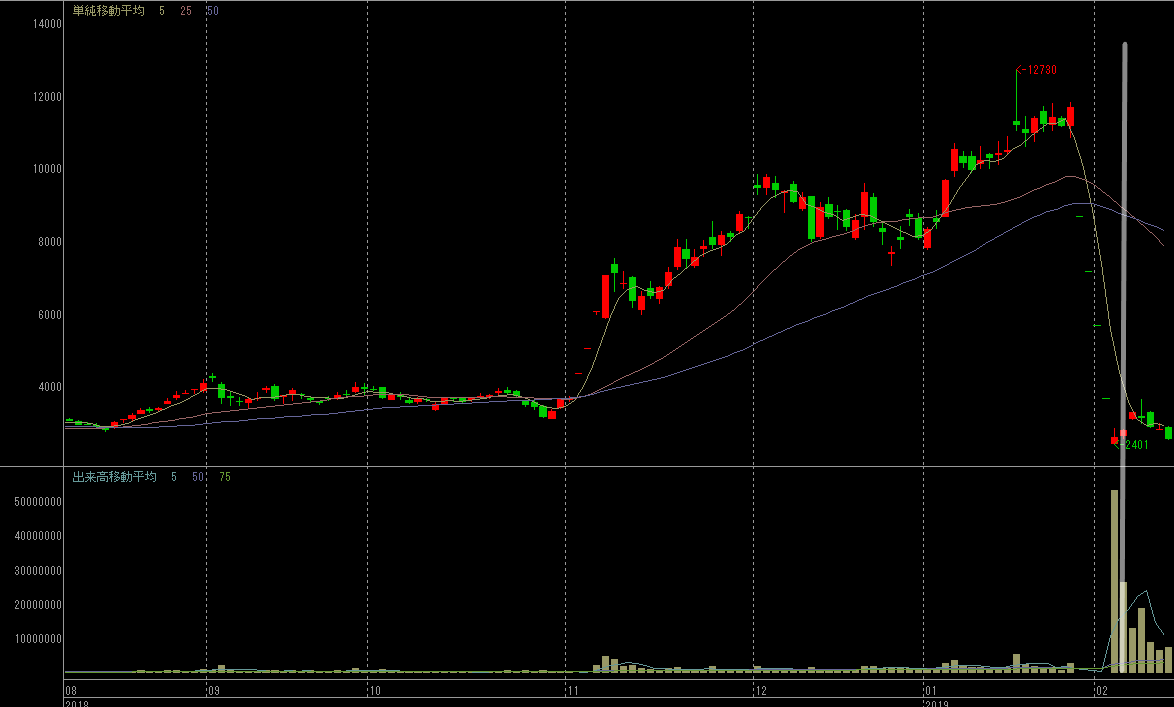 |
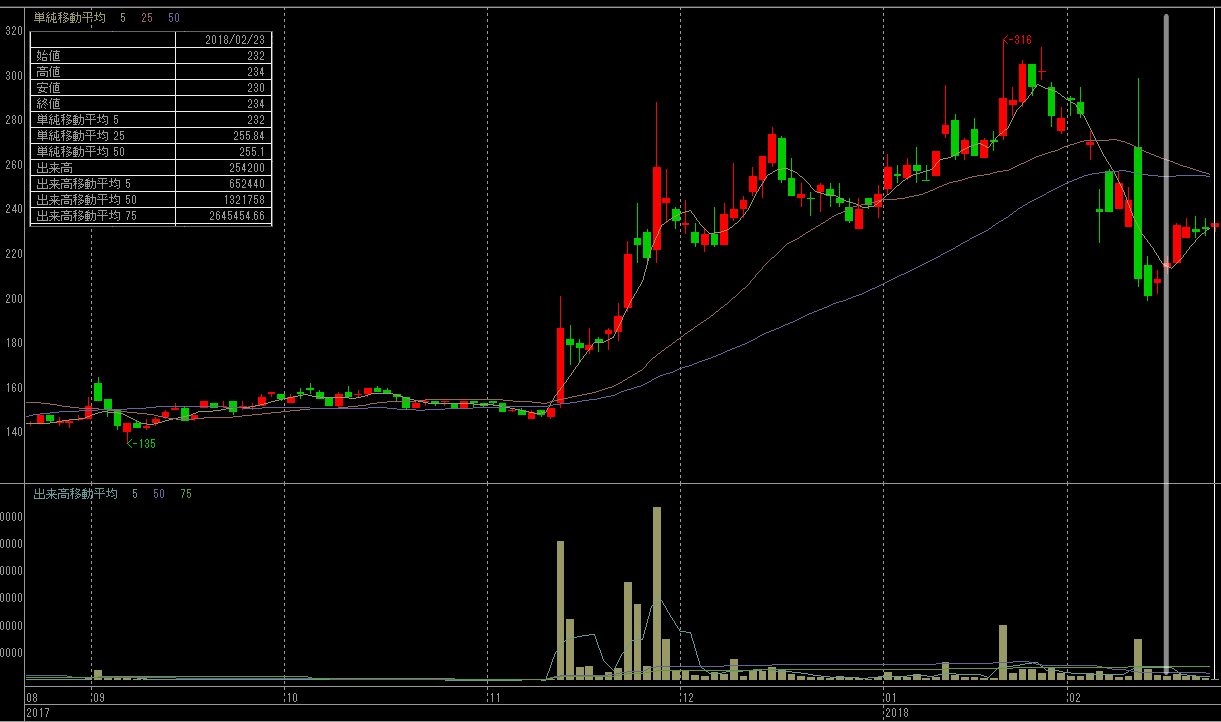 |
3038, 神戸物産
タピオカ銘柄です。
| 3038, 神戸物産, 2019-05-07 | 3098, ココカラファイン, 2018-01-09 | |
|---|---|---|
| A |  |
 |
| B | 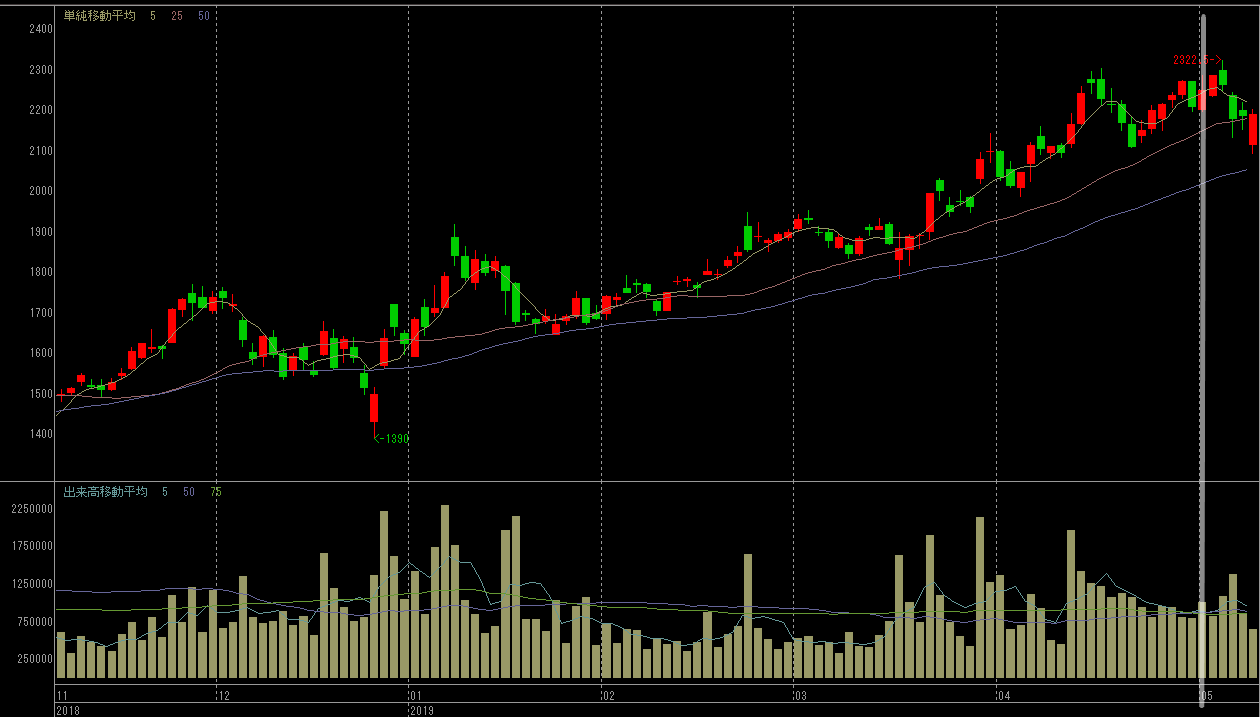 |
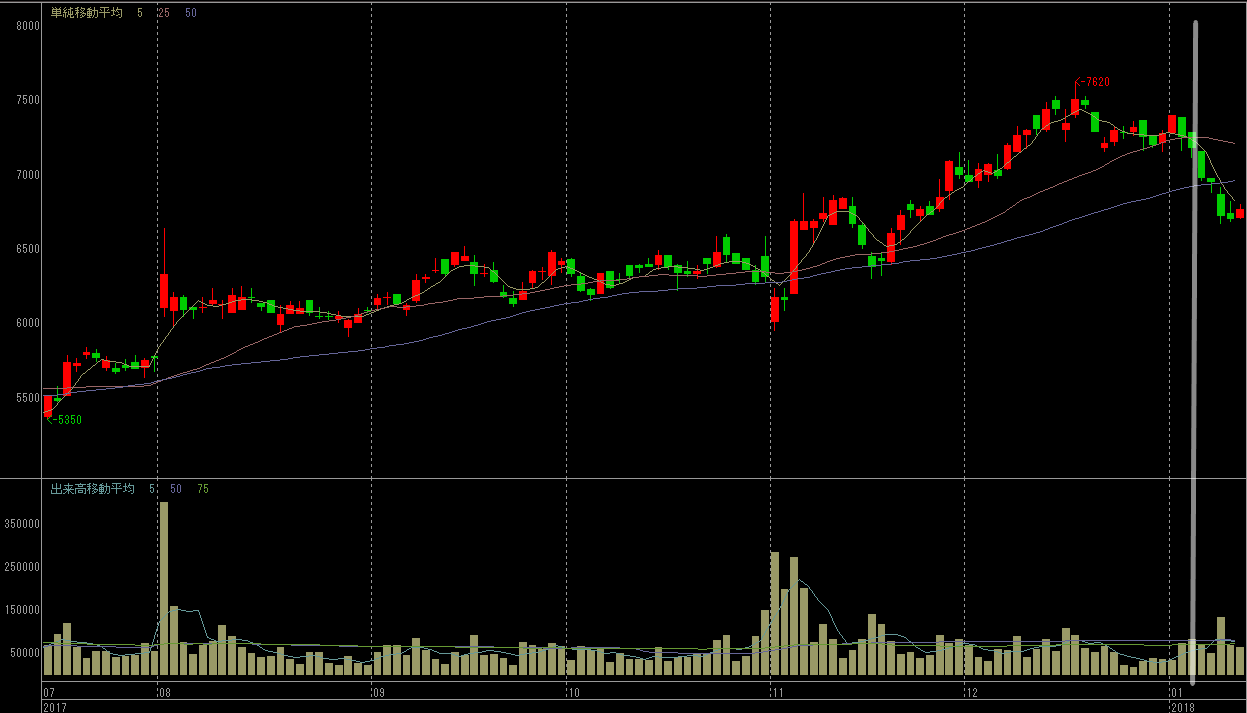 |
6166, 中村超硬
謎技術で6倍に爆上げした銘柄です。
| 6166, 中村超硬, 2019-11-05 | 7577, HAPiNS, 2019-10-08 | |
|---|---|---|
| A |  |
 |
| B | 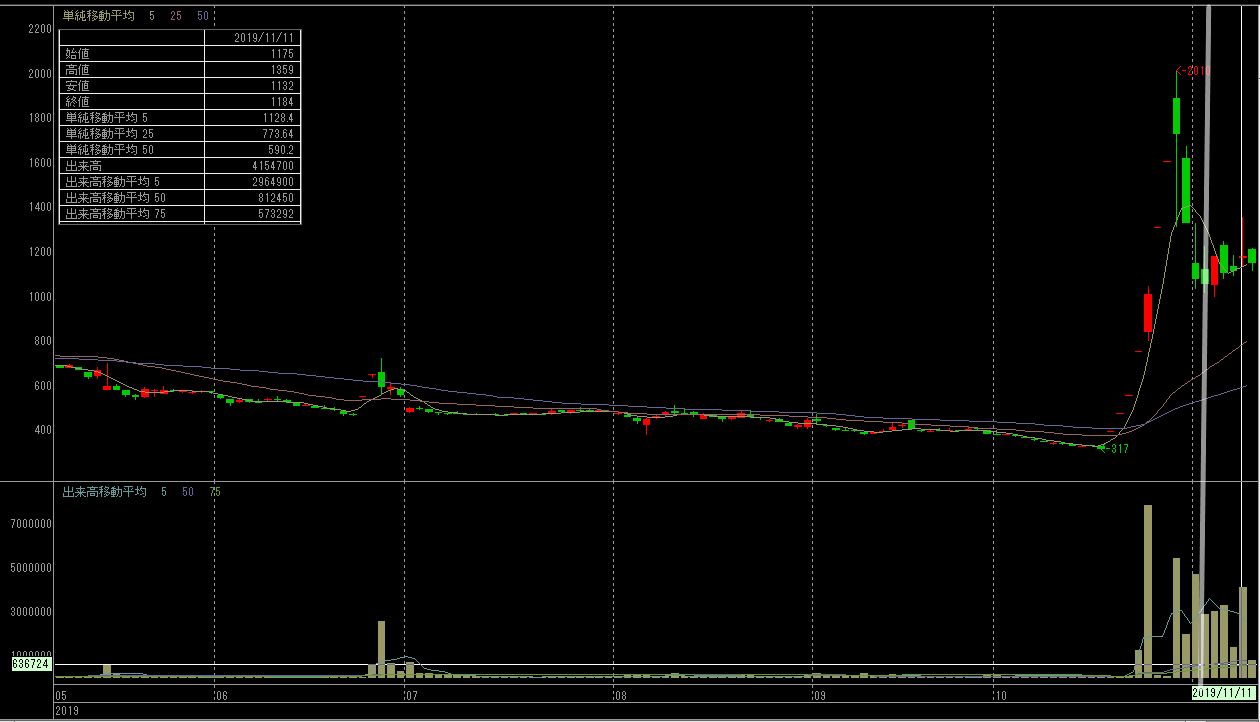 |
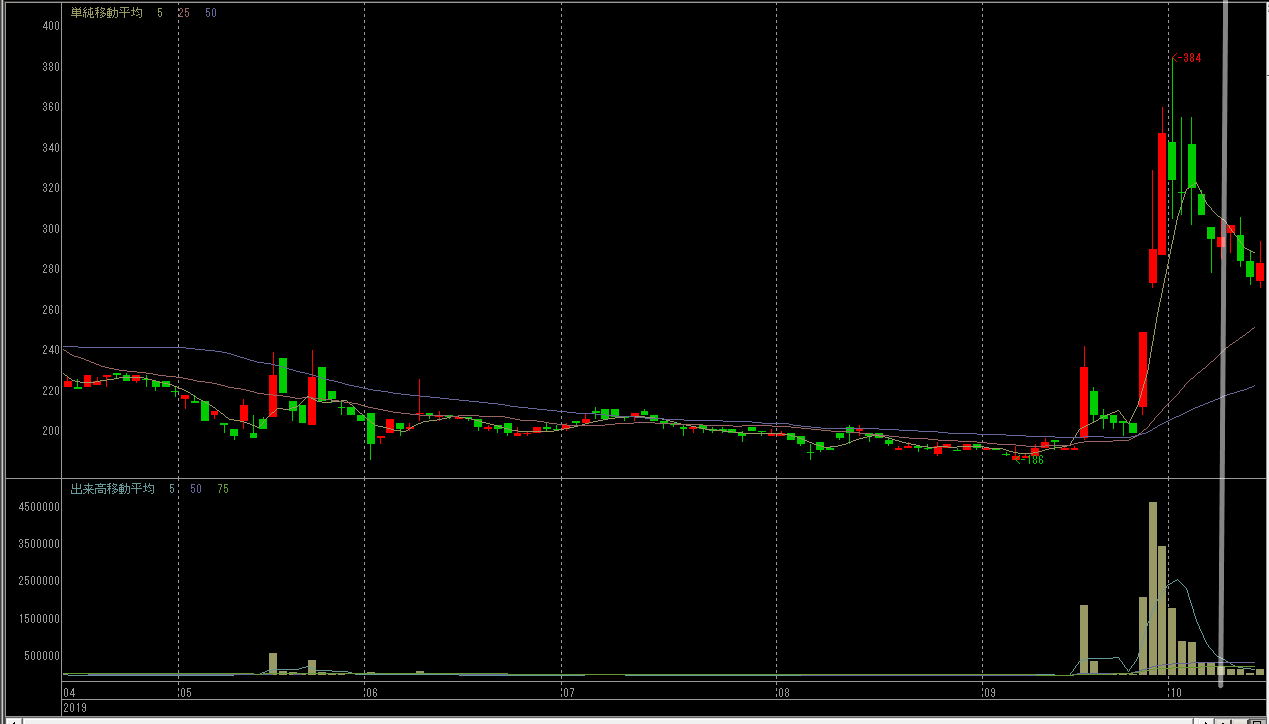 |
実験結果まとめ
検証項目Aの視覚的類似度検証についてはクエリと検索結果の時系列データは非常に似ていますので成功と言えるでしょう。検証項目Bについては関連があるかもしれませんしないかもしれません。
まとめ
時系列データの類似度計算方法を提案しました。成果としては類似度を計算できるだけでなく、時系列データを低次元ベクトルデータで表現できることもありますので、ここからさらに応用していくことで発展が見込めます。例えばベクトル化した時系列データにさらに機械学習をかけることで検証項目Bの変動予測を行ったり、銘柄ごとの特徴分析を行ったりと今後の取り組みはたくさんあります。
注意したいのは株価予測に一般的な時系列予測の手法や機械学習はアルゴリズムに逆手に取られる危険もあるかもしれません。というのも、機関投資家は意図的に買いまくって上げたり売りまくって下げたりできるのでその一手先まで読み切る工夫が必要かもしれません。