トポロジカルソートがわからなかったので調べてBFSで実装したのち、AtCoderの問題を解いてみた。

トポロジカルソート

実装できたけどワカッテハイナイ

#トポロジカルソートとは

閉路がない有向グラフの各有向辺が順方向になるようにソートすること

有向非巡回グラフ(DAG)とは
DAGとは、有向グラフ且つ閉路のないグラフのことである。これは、ある操作の手順を表す時に用いられたりする。DAGはトポロジカルソートをすることができる。

##参考サイト
トポロジカルソート
動的計画法によるトポロジカルソートの数え上げとπDDの構築
動的計画法入門
アルゴリズムとデータ構造

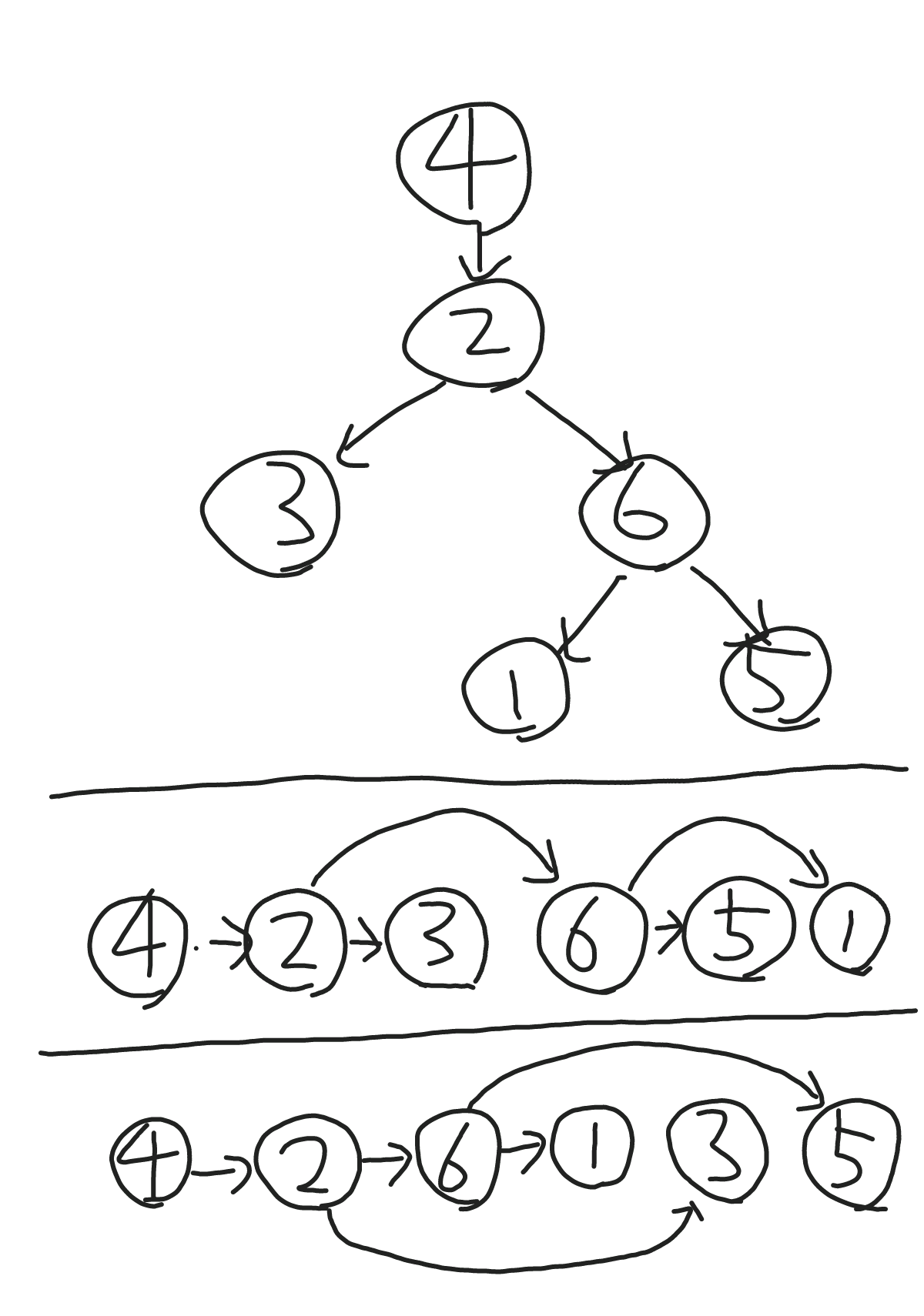
##トポロジカルソートとは、下図のような木を順に並べたものらしい
※トポロジカルソートの結果は、複数存在する場合がある（図ではトポロジカルソートの結果として、423651と426135の二つを記載）

• 上図の423615という木を例に、並べる順としては以下のようになる
  1. どこにも依存していないものが一番左(4)
     2. 隣接リストを作成した段階で入次数（いりじすう　と読むらしい）が0のものが根
  2. その次は、(4)のみに依存しているもの(2)
     3. (4)をリザルト用のListにaddし、(4)から(2)への辺を削除した結果、(2)の入次数は0になる
     4. (4)から(2)への辺を削除とは、「(4)をリザルトリストへaddする際に、(4)から他の頂点へののびている辺を隣接リストから探し、次の接続先の入次数をマイナスする」ことを指している。
  3. その次は、(2)のみに依存しているもの(3 または 6)
     4. (2)をリザルト用のListにaddし、(2)から(3)および(6)への辺を削除した結果、(3)および(6)の入次数は0になる
  4. その次は、(3) または (6)のみに依存しているもの([3]で(3)を選択しているなら(6)、[3]で(6)を選択しているなら、(2)のみに依存している(3)((6)と同列のもの)または(6)のみに依存している(1)または(5))
  5. 以下、全ての依存関係を確認していく

#BFSで実装してみる

※実装したら下記のAOJのサイトで確認することができる
GRL_4_B | トポロジカルソート | グラフ | Aizu Online Judge

	private void solveA2() {
		int v = nextInt();
		int e = nextInt();

		/*
		 *隣接リストの作成
		 */
		List<List<Integer>> adj = new ArrayList<List<Integer>>();
		for (int i = 0; i < v; i++) {
			adj.add(new ArrayList<Integer>());
		}

		for (int i = 0; i < e; i++) {
			int from = nextInt();
			int to = nextInt();
			adj.get(from).add(to);
		}
		// 入次数が0のものを判定するための配列
		int indegree[] = new int[v];
		// 入次数0を判定
		for (int i = 0; i < v; i++) {
			List<Integer> temp = adj.get(i);
			//iをfromとするnode達
			for (int node : temp) {
				//入次数の個数
				indegree[node]++;
			}
		}

		/*
		 * queueの作成
		 * 入次数0のものをqueueに詰める
		 * 入次数0から調査していく
		 */
		ArrayDeque<Integer> q = new ArrayDeque<Integer>();
		for (int i = 0; i < v; i++) {
			if (indegree[i] == 0) {
				q.addLast(i);
			}
		}

		//訪問済み頂点数
		int cnt = 0;

		// トポロジカルソートの結果
		List<Integer> res = new ArrayList<Integer>();

		/*
		 * BFS
		 */
		while (!q.isEmpty()) {
			// 接続先の頂点を探索開始
			int u = q.removeFirst();
			//入次数0なのでリザルトにadd
			res.add(u);

			/*
			 * この頂点の次の接続先の入次数を-する
			 * その結果、入次数=0となる場合はソートリザルトに追加し、次の探索に利用する
			 */
			for (int node : adj.get(u)) {

				indegree[node]--;
				if (indegree[node] == 0) {
					q.addFirst(node);
				}
			}
			cnt++;
			if (cnt > v) {
				System.out.println("graph内に循環有");
				return;
			}
		}

		for (int i : res) {
			out.println(i);
		}
	}

#AtCoderの問題を解いてみる

##D - Restore the Tree

トポロジカルソートを使う問題ということでチャレンジしてみる

結論としては、トポロジカルソートのロジックをほぼ改変なしで解けた

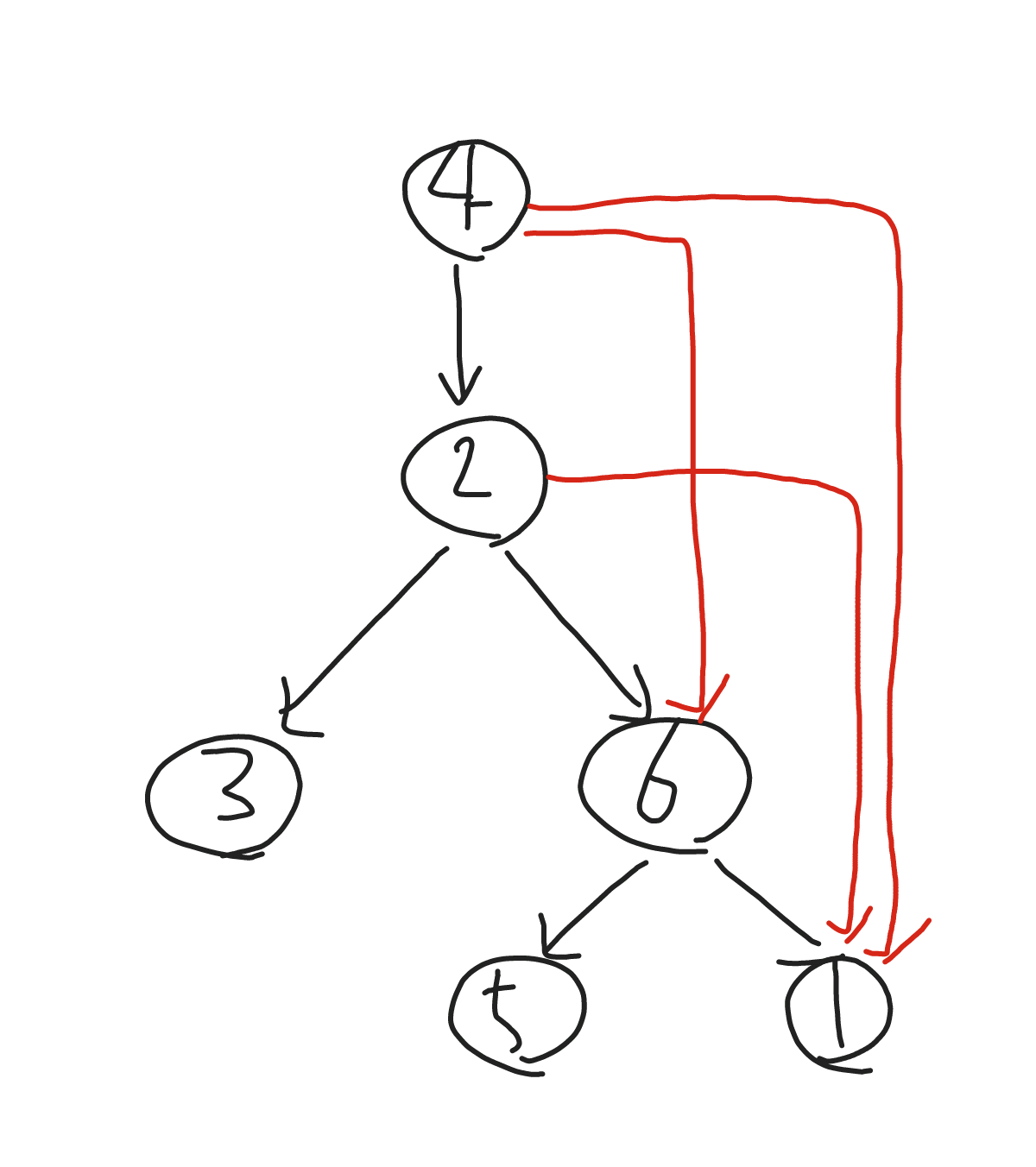
• 入力例 2 の構造は上記
  • 黒い辺が本来の木構造で、赤い辺はあとから足された辺
  • 元の木構造は「根以外の各頂点には、その親から一本の有向辺が伸びています」との記述があるので特定できる
• トポロジカルソートで並べるときに、自分の入次数が0になる時（自分に向かっている辺を削除した時）の頂点が親（うまい言い回しがわからない。。。）
  • 例えば、隣接リストを作成した時の(1)の入次数は3
    • (1)への辺があるのは(4)(2)(6)だが、トポロジカルソートしていくと、
    • (4)(2)(6)の順で(1)への辺を削除していく
    • (6)→(1)の辺を削除した時に(1)への入次数は0になる
    • (1)への入次数が0になった時の(6)が自分の親となる（複数の親がいるときは、根から一番遠い親が元の木構造の時の親）

AtCoder:全国統一プログラミング王決定戦予選(D - Restore the Tree)

	private void solveA() {
		int v = nextInt();
		int e = nextInt();

		List<List<Integer>> rinsetuList = new ArrayList<List<Integer>>();

		for (int i = 0; i < v; i++) {
			rinsetuList.add(new ArrayList<Integer>());
		}

		int[] indegrees = new int[v];
		for (int i = 0; i < v - 1 + e; i++) {
			int from = nextInt() - 1;
			int to = nextInt() - 1;
			rinsetuList.get(from).add(to);
			indegrees[to]++;
		}

		ArrayDeque<Integer> queue = new ArrayDeque<Integer>();
		for (int i = 0; i < indegrees.length; i++) {
			if (indegrees[i] == 0) {
				queue.addLast(i);
			}
		}

		int[] par = new int[v];
		int cnt = 0;
		while (queue.size() != 0) {
			int index = queue.removeLast();

			for (Integer nextDegree : rinsetuList.get(index)) {
				int nextCnt = --indegrees[nextDegree];
				if (nextCnt == 0) {
					queue.addLast(nextDegree);
					par[nextDegree] = index + 1;
				}
			}
			if (cnt > v) {
				out.println("graph内に循環有");
				return;
			}
		}

		for (int i : par) {
			out.println(i);
		}

	}